物理のエッセンス 力学 109番 P90【動画追加】

物理のエッセンス 力学 109番 P90

万有引力の位置エネルギーはよく知られているように無限遠をその基準としています。

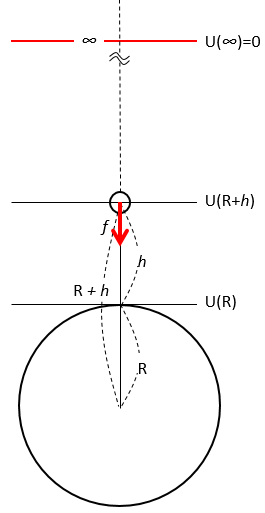
しかし、実際には位置エネルギーは、どこを基準にとっても良いはずです。（地球中心は引力が無限大となるため除きましょう）

この問題設定では万有引力の位置エネルギー基準を、地球中心から距離 $R$ の地表にとることとしています。

そして、地表高さ $h$ の地点にある質量 $m$ の物体が持つ位置ネルギーを求めるのが今回の問題です。

ここでは、解法として、

• 位置エネルギーの差から計算する方法（解答解説の方法）
• 地表から高さ $h$ の地点まで物体を運ぶときに外力がする仕事を計算する方法

の2つの方法で考えてみましょう。

動画解説

エネルギーの差から計算する方法

重力が $mg$ で変化しない場合

まず簡単のため、重力が $mg$ で変化しない場合について考えてみます。

---

位置エネルギー基準を図の最下点 $O$ にとります。

 

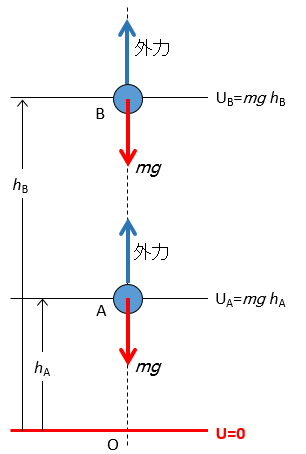
そうすると、高さ $h_A$ の $A$ 地点と高さ $h_B$ の $B$ 地点での重力による位置エネルギーをそれぞれ、$U_A$ 、$U_B$ として、

$U_A=mgh_A$　　　　$U_B=mgh_B$

と示されます。

エネルギー差 $U_B-U_A$ を計算してみると、

$$U_B-U_A=mgh_B-mgh_A=mg(h_B-h_A)$$

です。

---

$A$ を基準にとる

さてここで、$A$ を基準として、$B$ 地点の位置エネルギーを考えてみます。

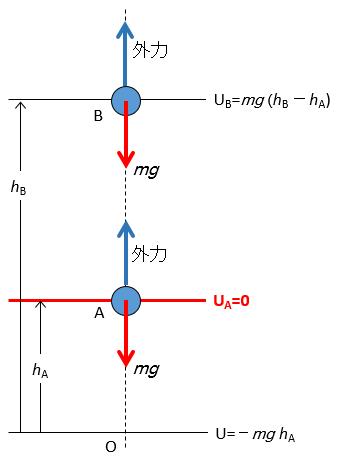
そうすると、$A$ 地点が基準、つまり $U_A=0$ なので、

$U_A=0$　　　　$U_B=mg(h_B-h_A)$

となることがわかります。

---

ここで、$A$、$B$ 2地点のエネルギー差 $U_B-U_A$ を考えてみます。
そうすると、

$$U_B-U_A=mg(h_B-h_A)-0=mg(h_B-h_A)$$

となり先ほどと同じです。

つまり、当然ですが2地点間のエネルギー差は、常に一定に保たれます。

これは位置エネルギー基準を $B$ にとっても同じです。
もっと言えば、どこに位置エネルギー基準をとっても同じになるはずです。

位置エネルギーの計算

つまり、今の基準での位置エネルギーを $U_A$、$U_B$ とし、新しく $A$ を位置エネルギー基準としたい場合、 $B$ の新しい位置エネルギーは、

$$U_B-U_A$$

$$(知りたい場所の位置エネルギー)-(基準にする場所の位置エネルギー)$$

とすればよいのです。

 

 

万有引力による位置エネルギー

本題に戻りましょう。

無限遠を基準として

地球質量 $M$、物体の質量が $m$ 、2物体間の距離が $r$ であるとき、万有引力 $f$ は、 $f=G\dfrac{mM}{r^2}$　で示されます。（万有引力定数を $G$ とする）  

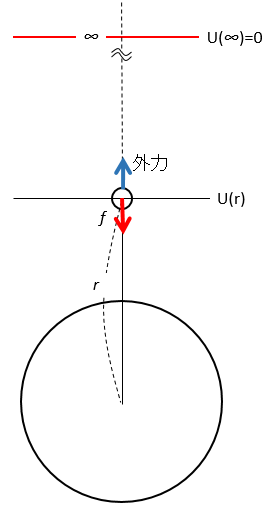
無限遠を基準とした場合、地球の中心から距離 $r$ の位置にある質量 $m$ の物体の持つ位置のエネルギー $U(r)$ は

$$U(r)=-G\dfrac{mM}{r}$$

で示されます。（なぜかについては補足参照）

したがって、無限遠を基準として、物体が地球中心から $R$ の距離である地表での位置エネルギーを $U(R)$、地表から高さ $h$ でのそれを $U(R+h)$ とすれば、

$U(R)=-G\dfrac{mM}{R}$  

$U(R+h)=-G\dfrac{mM}{R+h}$

となります。

ここで、新しく地表面 $R$ を位置エネルギー基準としたい場合、 $h$ の高さでの位置エネルギーは、

$$(知りたい場所の位置エネルギー)-(基準にする場所の位置エネルギー)$$

とすればよく、つまり、新基準位置での位置エネルギーを引けば良い　ので、

$$U(R+h)-U(R)$$

になります。

ですから、

\begin{eqnarray}
U(R+h)-U(R)&=&\left(-G\dfrac{mM}{R+h}\right)-\left(-G\dfrac{mM}{R}\right)\\\\
&=&GmM\left(-\dfrac{1}{R+h}+\dfrac{1}{R}\right)\\\\
&=&G\dfrac{mMh}{R(R+h)}
\end{eqnarray}

となり、位置エネルギー基準を地表に取る場合、地表から高さ $h$ の点における位置のエネルギーは、

$$U(R+h)-U(R)=G\dfrac{mMh}{R(R+h)}$$

となることがわかります。

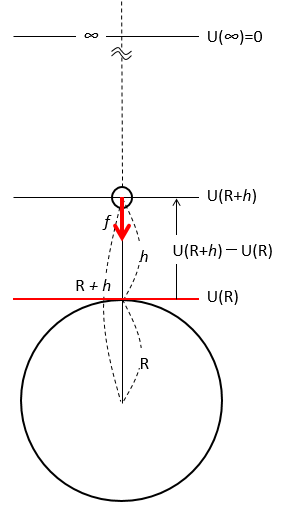
この場合、地表面での位置エネルギー $U(R)$ より、高さ $h$ の地点の位置エネルギー $U(R+h)$ は $G\dfrac{mMh}{R(R+h)}$ だけ「増加」している事がわかります。

位置エネルギーの基準を高さ $h$ にとったときの地表での位置エネルギー

無限遠を基準とした場合の位置エネルギーを $U(R)$、$U(R+h)$ とし、新しく高さ  $h$ を位置エネルギー基準としたい場合、 地表での物体のもつ位置エネルギーは同様に、

$$(知りたい場所の位置エネルギー)-(基準にする場所の位置エネルギー)$$

とすればよく、つまり、新基準位置の位置エネルギーを引けば良い　ので、

$$U(R)-U(R+h)$$

になります。

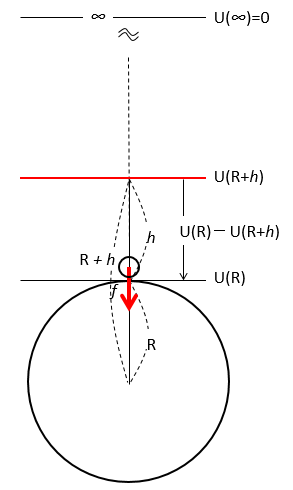
よって、

\begin{eqnarray}
U(R)-U(R+h)&=&\left(-G\dfrac{mM}{R}\right)-\left(-G\dfrac{mM}{R+h}\right)\\\\
&=&-GmM\left(-\dfrac{1}{R}+\dfrac{1}{R+h}\right)\\\\
&=&-G\dfrac{mMh}{R(R+h)}
\end{eqnarray}

となって、$-$ がつくことがわかります。

外力がする仕事を計算する方法

では次に、エネルギーと仕事の関係から位置エネルギーを求めてみましょう。

面積を出すのに積分計算を使います。

---

たとえば、最初の例でもあったように、一定の重力 $mg$ を受けている物体に外力を作用させて $h$ だけ高いところまで運ぶとき、その外力のする仕事が、位置エネルギーへと変化します。

このとき、ゆっくりと（等速で）物体を動かすわけですから、外力の大きさと重力はつり合っているとして構いません。

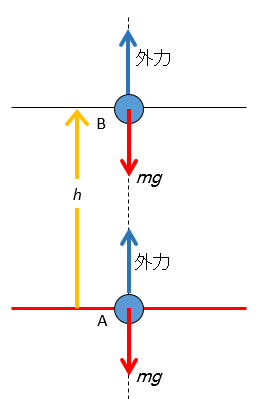
つまり、$外力の大きさ=mg$　となります。

そして、$仕事=力\times 距離$　ですから、

$$W=(mg)\times h =mgh$$

これが質量 $m$ の物体が、基準面からの高さ $h$ で持つ位置エネルギーとなります。

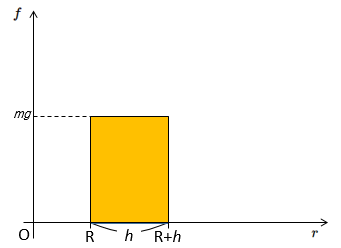
そして、図の色のついた四角形の面積で示されるのが仕事 $mgh$ です。

そして、位置エネルギーは、$mgh$ となります。

---

地表を基準とした場合の高さ $h$ における位置エネルギーを求めるのですが、
$R$ から $R+h$ まで物体を運ぶときに、外力がする仕事 $W$ を求めればよいことになります。

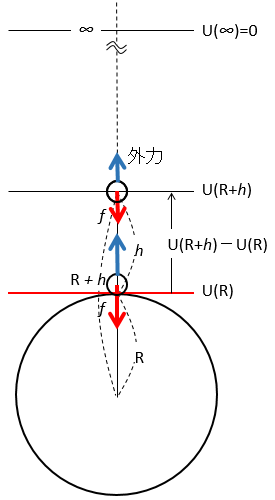
しかし、万有引力は　$f=G\dfrac{mM}{r^2}$　で示されるように一定ではありませんから、単純に　$仕事=力\times 距離$　で仕事を求めるというわけには行きません。

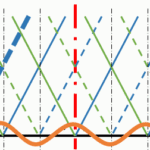
万有引力 $F$ と $r$ のグラフは次のようになります。

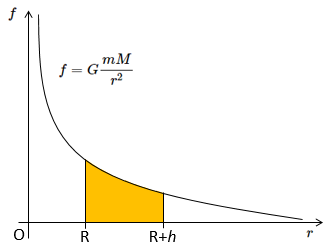
このときの仕事は図の色をつけた部分の面積で示されます。

ここでは、この面積を求めるために積分を用います。

仕事 $W$ は、図の色のついた部分の面積を求めればいいわけですから、

\begin{eqnarray}
W&=&\int^{R+h}_R{G\dfrac{mM}{r^2}}dr\\\\
&=&\left[-G\dfrac{mM}{r}\right]^{R+h}_R\\\\
&=&-GmM\left(\dfrac{1}{R+h}-\dfrac{1}{R}\right)\\\\
&=&G\dfrac{mMh}{R(R+h)}
\end{eqnarray}

となり、$G\dfrac{mMh}{R(R+h)}$　が、地表を基準とした場合の、地表から $h$ の高さにある物体の持つ位置エネルギーとなります。

補足　万有引力の位置エネルギー

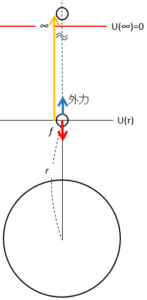
一般に、万有引力の位置エネルギーは無限遠をその基準としています。

したがって、地球の中心から $r$ の位置にある物体が持つ位置エネルギーの大きさは、外力を作用させて $r$ から$\infty$ までその物体を運ぶ仕事で示されます。

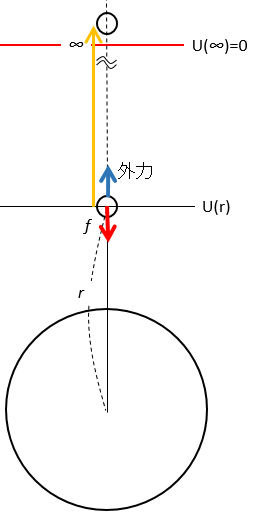
したがって、次のグラフにおける $r \rightarrow \infty $ の囲む面積を求めてやれば、必要な仕事の大きさがわかります。

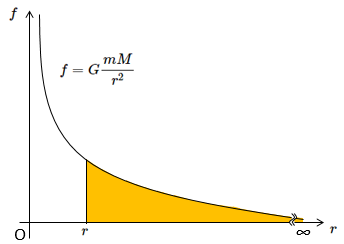
計算式は以下のようになります。

\begin{eqnarray}
W&=&\int^{\infty}_r{G\dfrac{mM}{r^2}}dr\\\\
&=&\left[-G\dfrac{mM}{r}\right]^{\infty}_r\\\\
&=&-GmM\left(\dfrac{1}{\infty}-\dfrac{1}{r}\right)\\\\
&=&G\dfrac{mM}{r}
\end{eqnarray}

さて、ここで $\infty$ を基準としているわけですから、万有引力による位置エネルギーはすべて $0$ 以下であり、最大値が $0$ となります。

よって、地球(質量 $M$ )中心から $r$ だけ離れた位置での質量 $m$ の物体がもつ万有引力による位置エネルギーは、

$U(r)=-G\dfrac{mM}{r}$

となるのです。（$G$：万有引力定数）

ここまで読んでくださりありがとうございます！

AmazonAmazonAmazon Amazon