物理のエッセンスの波動編の最後の問題 70番です。
ややイメージしづらい感がありますが、丁寧に図を用いて解説したいと思います。
エッセンスの次は良問・名問をおすすめします。
物理のエッセンス 波動 70番 P146
図のように、波が境界面に斜めにあたり、反射しています。波長 $\lambda$、速さ $v$ とします。
入射角と反射角はともに $\theta$ です。
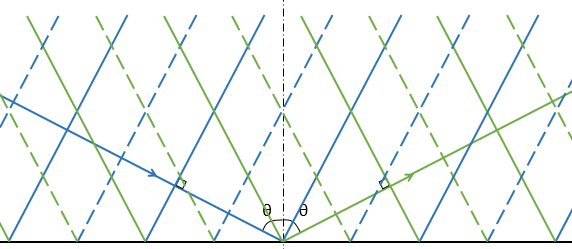
青い色の波は入射波、緑の色の波は反射波を示しており、反射は自由端反射です。
実線は波の山を、点線は波の谷を示しています。
問題は、
- 図の波の強めあう位置と弱めあう位置を図示し、強め合う位置の面間隔 $\Delta x$を求めます。
- 境界面上を伝わる波の速さ $V$ とその伝わる様子を考えます。
考え方
動画解説
面間隔 $\Delta x$
波のようすを知るには今現在の波をほんの少しだけ、それぞれの進行方向にずらして考えてやります。
この問題の場合も、青い波と緑の波を進行方向に少しだけずらしてみましょう。
そして、波の一部の青の波の山(谷)と緑の波の山(谷)が重なるところに◯をつけます。
そうすると、図のようになります。
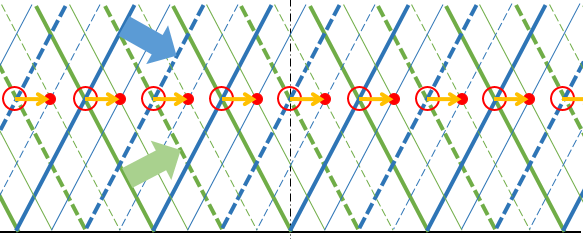
つまり、◯印をつけたところは図の右側に進行していくことがわかります。
強め合う面と弱め合う面はともに境界面に対して平行です。
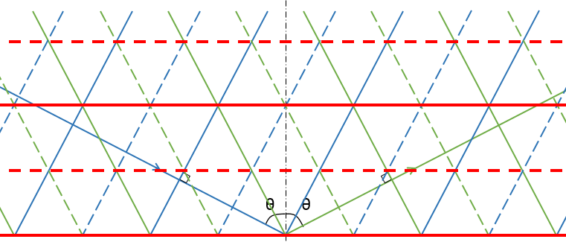
図の赤の実線は強め合う面で、点線は弱め合う面です。
そしてこれらは定常波ではなく、図の右に進行する進行波です。
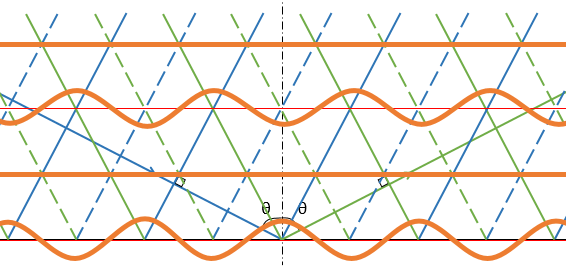

これは「2点波源の干渉」の記事における、2点波源の一直線上の波源の外側における、進行波に似ています。
詳しくはこの記事を参照してください。

境界面上の山や谷に注目して、アニメーションで示して見ましょう。
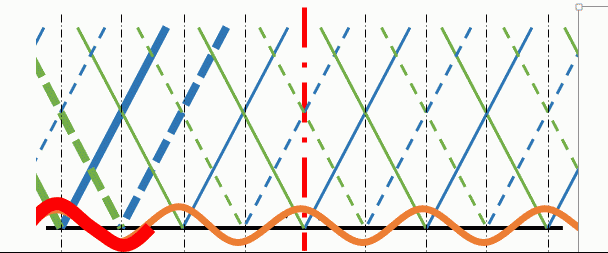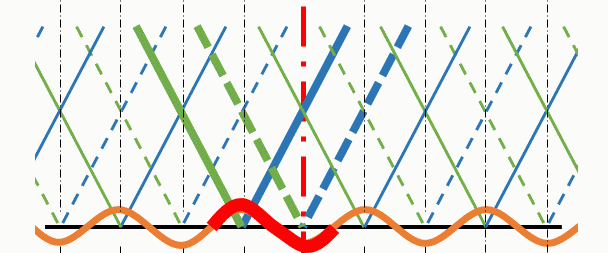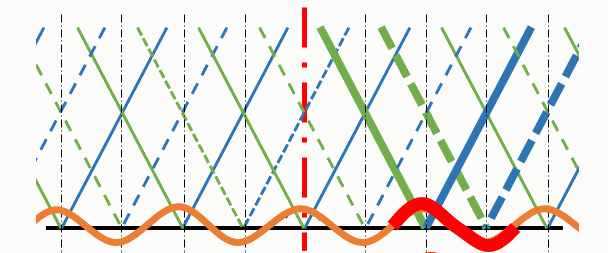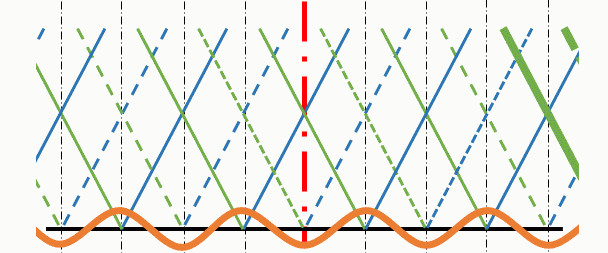
赤い波に注目すると、図の右方向へ進行しているようすがよく分かると思います。
したがって、問題の強め合う面と強め合う面の間隔 $\Delta x$ は次の図から求めることができます。
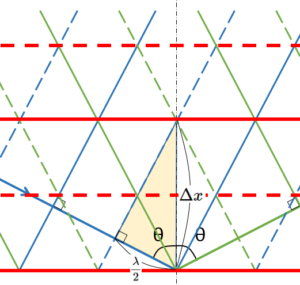
図の色のついた直角三角形から考えます。
青の点線と実線の間隔は $\dfrac{\lambda}{2}$ で。面間隔は $\Delta x$ ですから、
$$\cos \theta =\dfrac{\dfrac{\lambda}{2}}{\Delta x}$$
\begin{eqnarray}
\Delta x&=&\dfrac{\dfrac{\lambda}{2}}{\cos \theta}\\\\
&=&\dfrac{\lambda}{2\cos \theta}
\end{eqnarray}
進行波の速さ
次に境界面上を図の右に進行する波の速さを求めましょう。
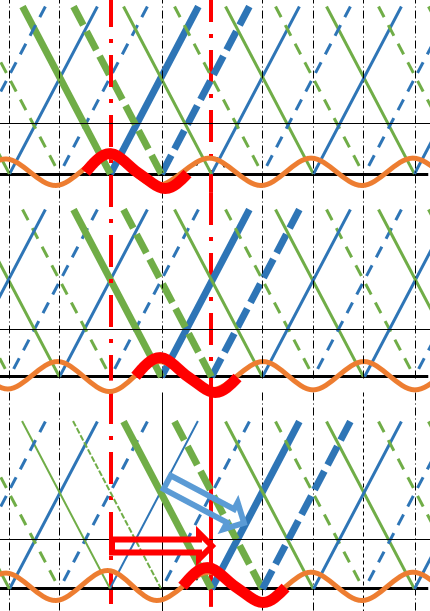
⇒ が $1\lambda$ 進むとき、⇒ も $1\lambda$ すすみます。
したがって、波の周期は 赤も青も同じです。
ということは、赤い波の波長を $\lambda^{\prime}$ とすれば、
$$v=\dfrac{\lambda}{T}$$
$$V=\dfrac{\lambda^{\prime}}{T}$$
となることがわかります。
片々割って、
\begin{eqnarray}
\dfrac{V}{v}&=&\dfrac{\dfrac{\lambda^{\prime}}{T}}{\dfrac{\lambda}{T}}\\\\
&=&\dfrac{\lambda^{\prime}}{\lambda}
\end{eqnarray}
ここで、次の直角三角形を考えます。
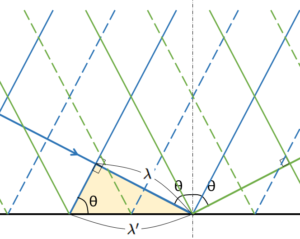
このとき、 $\sin \theta =\dfrac{\lambda}{\lambda^{\prime}}$ より、
\begin{eqnarray}
\dfrac{V}{v}&=&\dfrac{\lambda^{\prime}}{\lambda}\\\\
V&=&\dfrac{v}{\sin \theta}
\end{eqnarray}




































コメント