センター試験・共通テストなどではグラフの選択問題が出る可能性があります。
過去の問題を見ると、なかなか難しいというか、勘違いするものが多く、カンで解いてはいけません。
物理のエッセンス力学編10番
問題概要
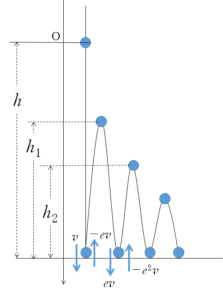
高さ $h$ から物体を自由落下させる。
床と物体の反発係数を $e$ とするとき、
- 最初に衝突した後に跳ね上がる最高点の高さ $h_1$
- 床と2度目の衝突後の最高点の高さ $h_2$
を求めよ。

$v-t$ グラフについての記事・・・こちらも参考にどうぞ
解説
$v-t$ グラフを描いてみましょう。

そのまえに、ここで反発係数について復習です。
反発係数について
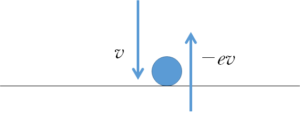
反発係数 $e$ のとき、はね返る前の速度 $v$ 、はね返ったあとの速度 $v’$ とすると、
- $e=-\dfrac{v’}{v}$
- $v’=-ev$
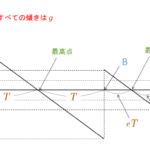
$v-t$ グラフを描くにあたって注意すべきことは、グラフの傾きは全ての場合で $g$ である!! ということです。
これは空中においては物体は重力だけを受けて運動していることに起因しています。
物体は最初に床に衝突する前の速度が $v$ で、衝突後瞬間的に速度 $-ev$ で反転します。
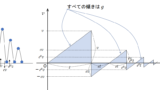
これらを $v-t$ グラフに描くと次のようになります。
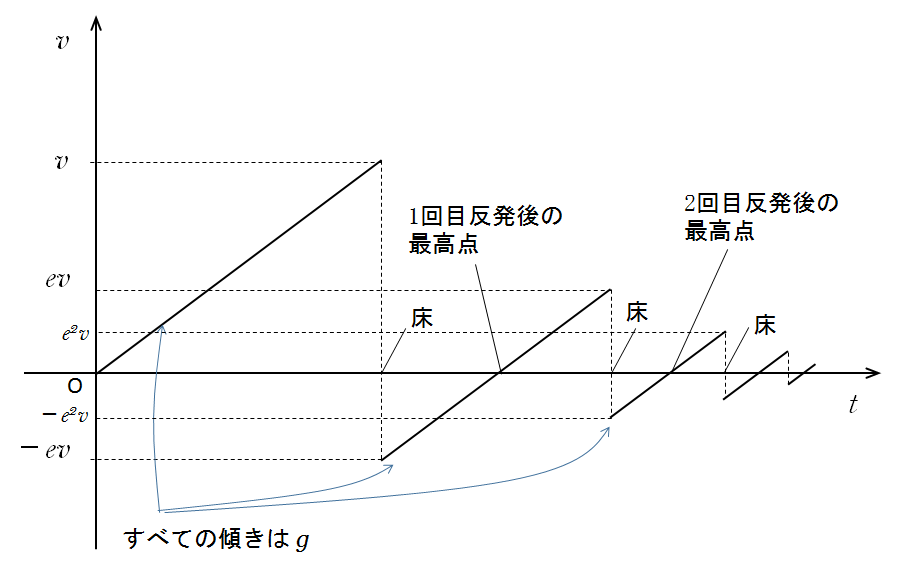

このとき、グラフの傾きは全ての場合で $g$ で同じです。
そのため、グラフと $t$ 軸とがつくる 三角形は全て相似 です。
ここで、三角形の縦の長さ(物体の速さ)が1回の衝突ごとに $e$ 倍されていくわけですから、相似形の三角形の横の長さ(時間)も $e$ 倍されていきます。
すわなち、
- 1回目の衝突直前の速さを $v_0$ 落下に要する時間を $t_0$
- 1回目の衝突後の直後の速さを $v_1$ 最高点までに要する時間を $t_1$
- 2回目の衝突後の直後の速さを $v_2$ 最高点までに要する時間を $t_2$
とすると、
- $t_1=et_0$ $v_1=ev_0$
- $t_2=et_1=e^2t_0$ $v_2=ev_1=e^2v_0$
ということですね。
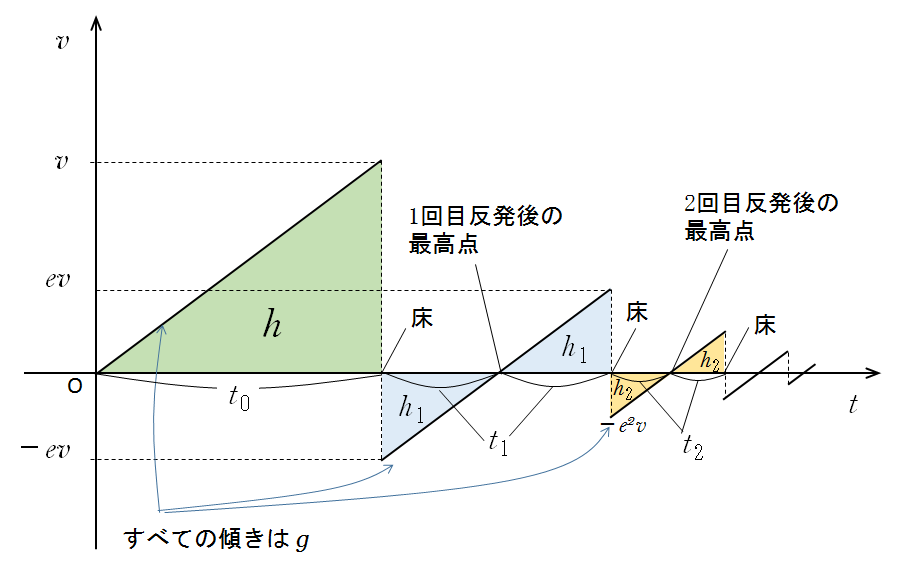
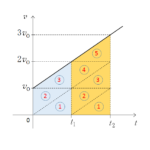
$v-t$ グラフで $t$ 軸と囲む面積は距離(変位)を示しています。
三角形面積 = 底辺 × 高さ ÷ 2 ですから、三角形面積は $e^2$ 倍ずつ変化することがわかります。
そうなるとカンタンですね!
答え
最初の落下距離
$\mathrm{図の緑色の三角形の面積}= h$1回目の衝突後の最高点
$\mathrm{青の三角形面積} = e^2h$1回目の衝突後の最高点
$\mathrm{オレンジの三角形面積}=e^4h$

この問題では $v-t$ グラフを描くことができれば、計算は全て不要なのです。
$v-t$ グラフに関してさらに詳しく説明しています。




































コメント