今回は、加速する電車内での風船の動きを考えましょう。
直感は正しいか?・・・の続編です。
あなたの直感や常識を試してみて下さい。常識テストはこちら
慣性力についての解説はこちらへ!

風船はどちらへ傾くか?慣性力で考える

ヘリウム入の風船をもって電車に乗ります。
電車が停止状態から加速し始めました。
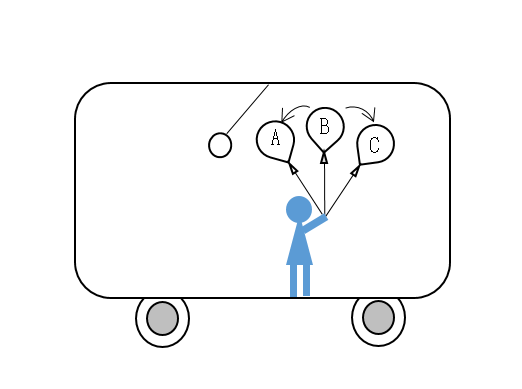
さて、風船は図のどちらに傾くでしょうか?
また、それはなぜでしょうか?
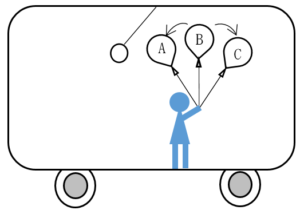
選択肢
- A
- B
- C
- その他 場合による
理由を考えましょう!

答え
C です。
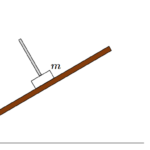
図で、天井から吊るしたおもりが左へ傾いているので、この電車は図の右方向に加速しています。
それなら、A!!と思った人はいませんか?
確かに私達の日常の経験から、図の右方向に電車が急発進すると、後ろにひっくり返りますよね。
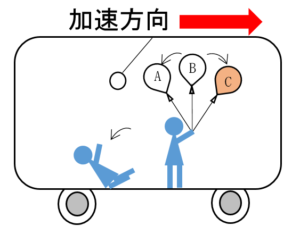
でも、この場合は、風船はCの方向に傾きます。
これは慣性力を考えてみればわかります。
慣性力に関しては次の記事でも解説しています

電車が停止または等速直線運動していると風船の浮かぶ向きは、真上のBの向きです。
つまり、この風船は浮力により、重力と反対方向に浮かんでいるということですね。
では、加速する車内での慣性力を考えてみます。
慣性力は、加速度の方向と一直線上逆向きに大きさ $ma$ ではたらきます。
図で、天井から吊り下げられたおもりにはたらく力を、慣性力も含めてあらわしてみました。
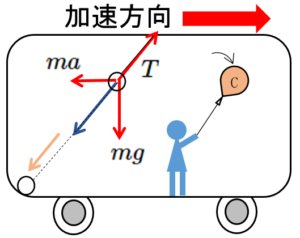
車内の人から見て天井から吊り下げられた物体は静止しています。
したがって、物体にはたらく重力 $mg$ と慣性力 $ma$ の合力(図の青の矢印)が、糸の張力 $T$ とつり合っているのがわかります。
この状態でもし糸が、プツンと切れれば物体は図の点線方向に真っ直ぐ落ちることになります。

これは試験でも、ちょくちょく出題されます。
ここでよく理解しておいて下さい。
つまり、車内の人にとって、加速状態ではこの青の矢印の方向が「下」となります。
なので、風船はこの反対方向の「上」・・・すなわちCの方向に浮くのです。

ちなみに、車内の人にとっての「重力加速度」は $a$ と $g$ をベクトル的に合成したものです。
よって、その大きさは、$\sqrt{a^2+g^2}$ となります。
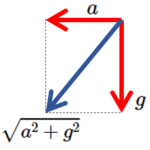
もし車内で振り子を振らせると、その周期は
$T=2\pi \sqrt{\dfrac{l}{\sqrt{a^2+g^2}}}$
ですね!!
エレベータと慣性力についてはこちらへ!

実際にやってみると・・?
理論的には正しくても、実際にこの実験を電車内や自動車内でやってみてもあまりうまくいきません。
自動車などで、直線上で加速度を一定に保つのは難しく、かつ、すぐに自動車のスピードが上がりすぎてしまうからです。
ほんの短い時間しか等加速直線運動できません。
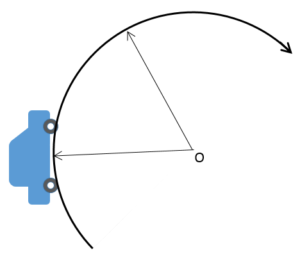
そこで一定半径で回転するように自動車を運転(等速円運動)してやれば、非常に簡単にしかもキレイに安定したヘリウム風船を見ることが可能です。

なぜでしょうか?

等速円運動も加速運動だからですね!
加速度の大きさは一定で、
向きは回転中心に向いています。
やり方は
自動車でカーブを等速で走る・・・それだけです。
その際になるべく、回転半径が一定になるようなカーブを選ぶと良いでしょう。
スピードは制限速度を守ってくださいね。それでも十分にキレイに実験が再現できます。

さて、問題です。その際に風船はどのように傾くでしょうか?

わかりました!
回転の内側にかたむきますね!



































コメント