SpaceX-Imagery / Pixabay
子供が積み木を押して遊ぶとき、積み木を押す手を離せばすぐに積み木は止まる・・・・このことから、子供は知らず識らずのうちに、物体を継続的に運動させるためにはその方向に力を加えてやることが絶対必要だと「学ぶ」のです。
これは子供にとっては自然な考え方です。
しかし、物理の教科書には違うことが書かれていますね。
慣性の法則とは
慣性の法則
物体に外部から力が働かないか、あるいは働いてもつりあっている場合、静止している物体は静止し続け、運動している物体は等速直線運動を続ける。
このことから読み取れることは、、物体に力が働かなければ永久に等速直線運動する?・・・・ということです。
宇宙空間を想像し、何も抵抗がない場合を想定できても、慣性の法則がなりたつなど、昔の私にはどうにも信じられませんでした。
「動力もないのに永久に運動するのか!?」
それは自分の目で見、そして自ら経験したことが土台だからだと思います。
でも目で見たからといって、それがすべて真実だとは限りません。
その証拠に、マジックは素晴らしい奇跡を見せてくれますが、それが真実ではないことはみんなが知っていることです。
私達はこういった誤った自然観をどれだけ打ち壊すことができているのか?
このとこを意識するかしないかで、物理の理解にはそれこそ雲泥の差が生まれます。
ガリレオの思考実験
ガリレオは慣性の法則の概念に到達していました。
それは彼の思考実験によるものです。
思考実験とは、頭の中で行う実験です。
したがって、理想的な条件を設定することができます。
ガリレオはどのような思考実験を行ったのでしょうか?
ここではその一つについて示します。
なめらかな面をもつ斜面を使い、ボールを転がします。
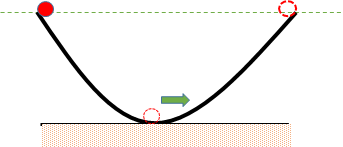
抵抗がなければボールは同じ高さまで上がるはずです。
次に、距離を伸ばしてみます。
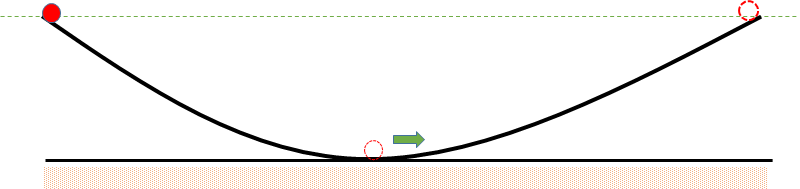
この場合も、同様に同じ高さまで上がると考えられますね。
ではこれを無限にまで伸ばしたら・・・・・
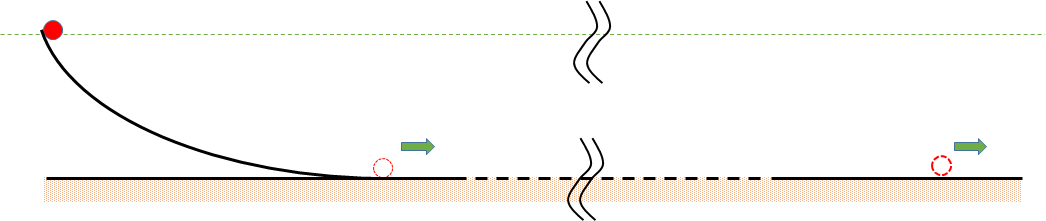
ボールはどこまでも転がるのではないか?
ボールに摩擦や空気抵抗などがない場合は、永遠に等速直線運動しそうです。
曲がるときは力がいりそうですから、力が働かない場合、やはり曲がることもなさそうですね。
慣性という概念
さらに、慣性は今の運動状態の変え難さ、というようなニュアンスで使うこともありますが、これはどういうことでしょうか。
運動方程式を使えるなら、次のように考えてみてはいかがでしょうか。
$ma=F$
ですから、力 $F$ がはたらくと加速度が変化します。
今、等速度というときは加速度0を意味しますね。
なので、力 $F$ を与えることで慣性による等速直線運動の状態を破ることになります。
その時の物体の動きは加速度が大きいほど急激な運動をします。
$a=\dfrac{F}{m}$
ですから、力 $F$ が同じでも質量 $m$ が大きいほど加速度は鈍ります。
したがって、質量 $m$ が大きいということは今の状態を変化させにくい、動かしにくいということを表しているのです。
つまり、慣性とは今の状態を変化させるときの、その変え難さを示していると言えるでしょう。
そのため、このようにして定義される質量を慣性質量と呼びます。
他には、重力ではかる、重力質量という概念もあります。
これらは、定義が異なるため値が違ってもおかしくないはずですが、不思議なことにほとんど一致していることがわかっています。
これはニュートン力学では偶然の一致ですが、そうではなく意味をもたせたのがアインシュタインです。
これにより、一般相対性理論の着想を得たのですね。









































コメント