クインケ管

クインケ管

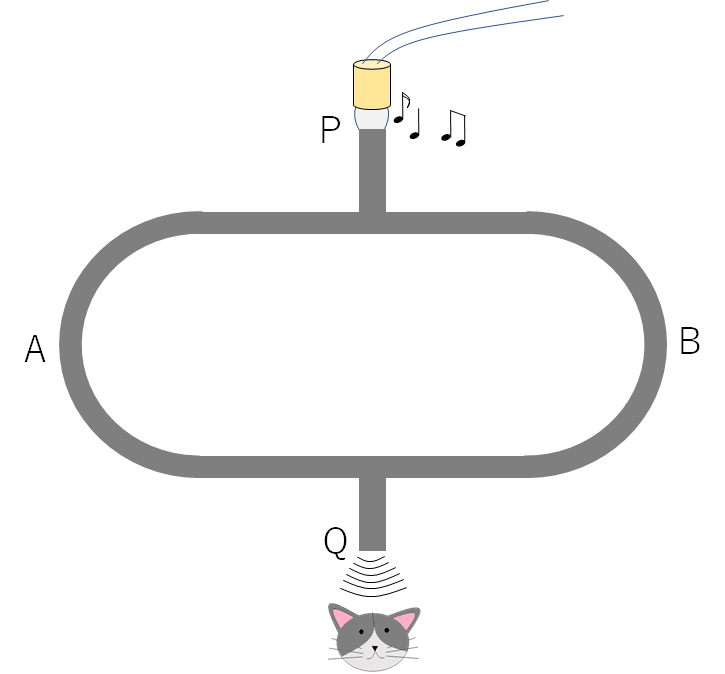
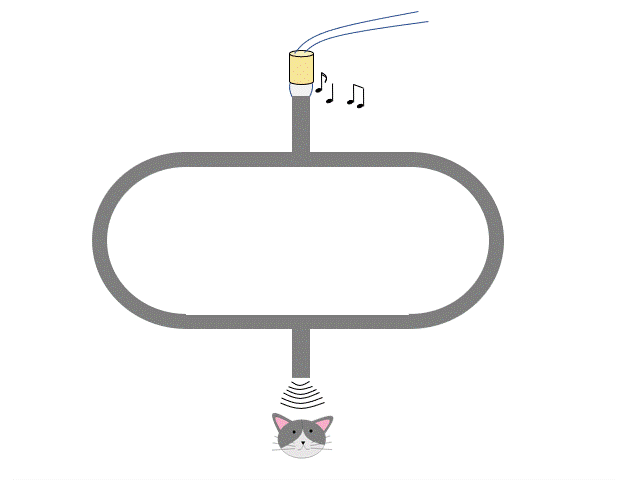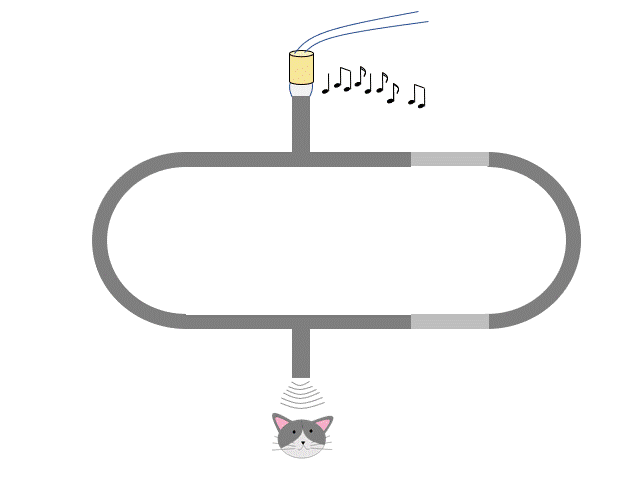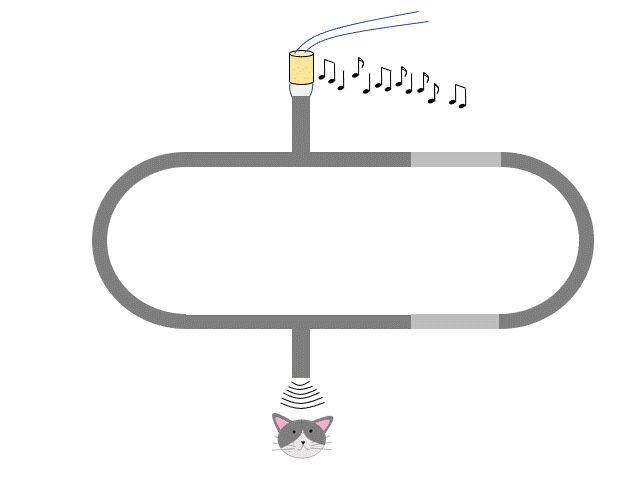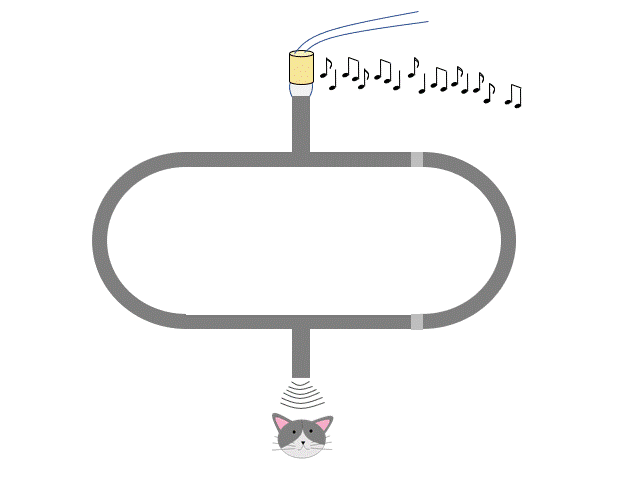
クインケ管とは図のような装置です。

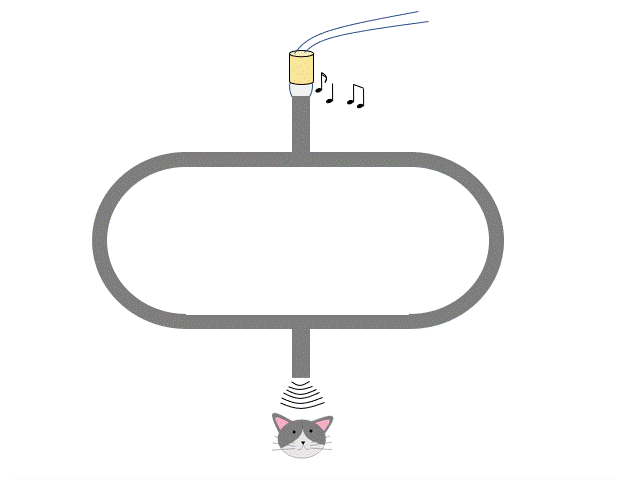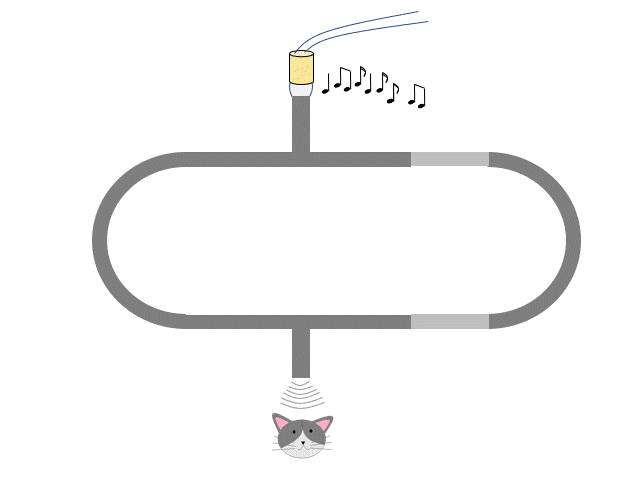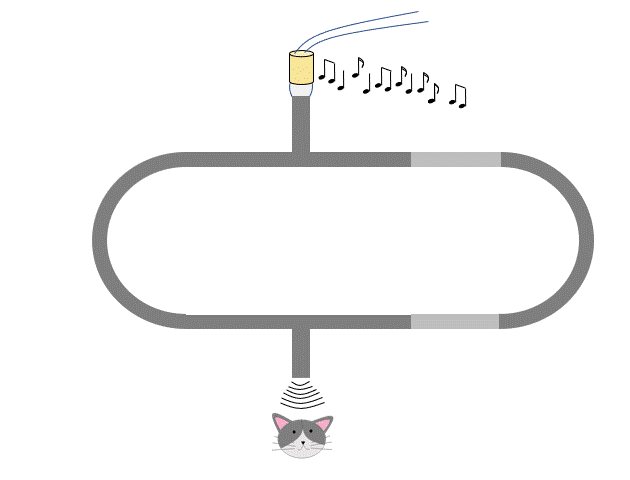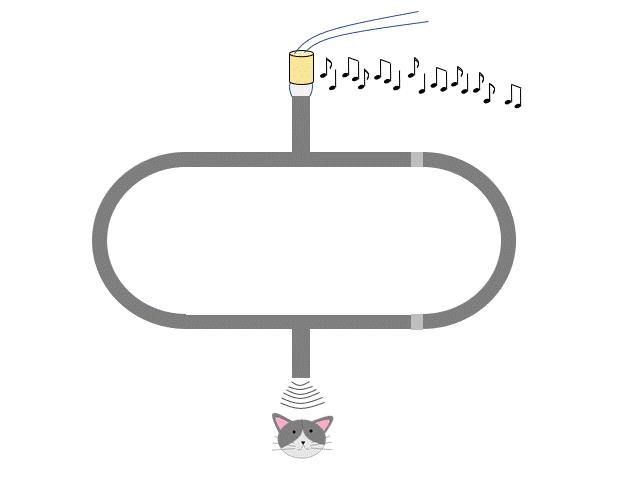
U字型の中空の管を２つ組み合わせるのですが、片側の管はトロンボーンのようにスライドして長さを変えられるようになっています。

この管の片方から音を入力します。

そうして、他方で聞いてみるのですが、管を出し入れすると音が小さくなったり大きくなったりすることに気が付きます。

これはなぜ起こるのか？ということについて今回は解説します。

干渉条件

音は P から入力されて左右の管を通り Q で再び出会い干渉します。

次の図のように、管を完全に入れた状態では左右の経路 PAQ と PBQ は同じ距離であるので、左の経路と右の経路を通った音は同位相で Q に到達します。

よって、この場合は音は大きく聞こえます。

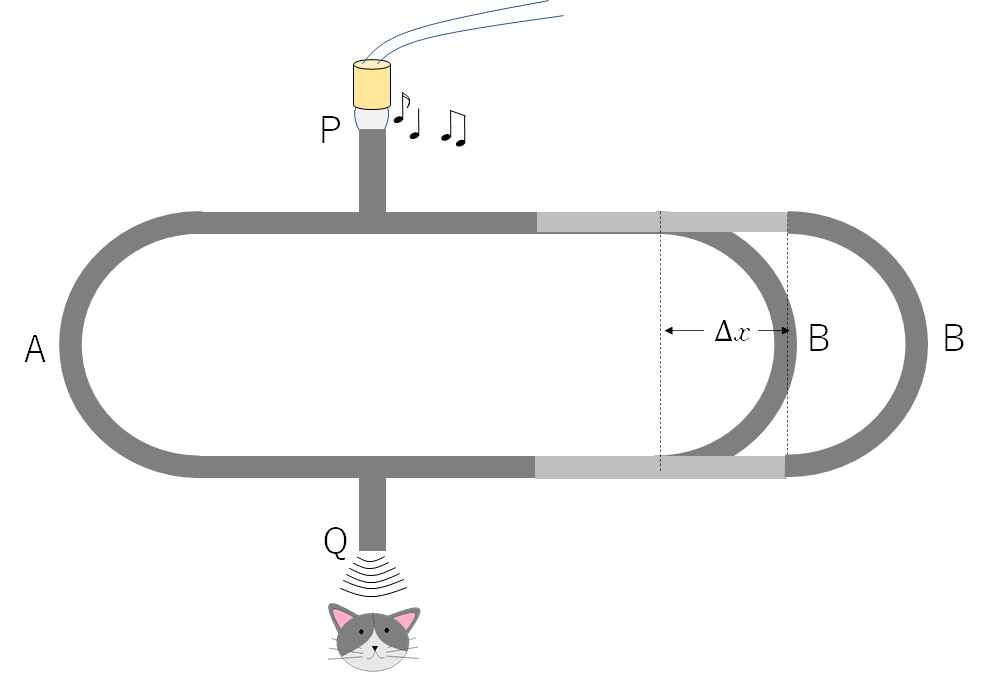
次に、右の管を $x$ だけ引き延ばしたときの干渉条件を考えましょう。

$x$ だけ引き延ばした状態では、左右の経路 PAQ と PBQ の経路差は $2x$ になります。

したがって、ヤングの実験と同じように考えて、

大きくなる　$2x=m\lambda$

小さくなる　$2x=m\lambda + \dfrac{1}{2}\lambda$

$m=0,\:1,\:2,\:3,\:\cdots\cdots$

と考えられます。

音の大小と管の間隔

ここで、$m$ 番目の $x$ を $x_m$ と書くことにします。

そうすると、

音が大きくなる時

大きくなる　$2x_m=m\lambda$

より、$x_m=\dfrac{m}{2}\lambda$

間隔を $\Delta x$ とすると、

$\Delta x = x_{m+1} \:-\: x_m $

$~~~~~~= \dfrac{m+1}{2}\lambda \:-\: \dfrac{m}{2}\lambda$

$~~~~~~=\dfrac{\lambda}{2}$

音が小さくなる時

小さくなる　$2x=m\lambda + \dfrac{1}{2}\lambda$

より、$x_m=\dfrac{m}{2}\lambda + \dfrac{1}{4}\lambda$

間隔を $\Delta x$ とすると、

$\Delta x = x_{m+1} \:-\: x_m $

$~~~~~~=\left( \dfrac{m+1}{2} \lambda + \dfrac{1}{4} \lambda \right ) \: – \: \left ( \dfrac{m}{2} \lambda + \dfrac{1}{4} \lambda \right )$

$~~~~~~=\dfrac{\lambda}{2}$

つまり、音が大きくなる間隔も小さくなる間隔も、管を $x=\dfrac{\lambda}{2}$ だけ出し入れしたときに生じます。

また、「音が大きくなった後、小さくなる」・「音が小さくなった後、大きくなる」時、管は $x=\dfrac{\lambda}{4}$ だけ出し入れされています。 下図