屈折の法則ですが、波動の基本法則なので皆さんご存知のことと思います。
ただ、実際に問題に使用するときに間違いが結構多いんですね。
ここでは、特に光の場合にこうすれば間違わないという方法をお教えしましょう。
動画で解説
屈折の法則
図のように光が屈折したとします。
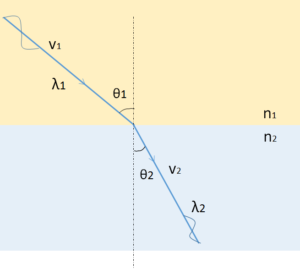
皆さんご存知の屈折の法則とは以下のようなものですね。
\begin{eqnarray}
n_{12}&=&\dfrac{\sin \theta _1}{\sin \theta _2} \\
\\
&=&\dfrac{\lambda _1}{\lambda _2}\\
\\
&=&\dfrac{v_1}{v_2}\\
\\
&=&\dfrac{n_2}{n_1}\\
\end{eqnarray}
ここで、光学において、 $n_1$ や $n_2$ は絶対屈折率というものです。
これは光が屈折する場合、物質の真空に対する屈折率として定義されています。
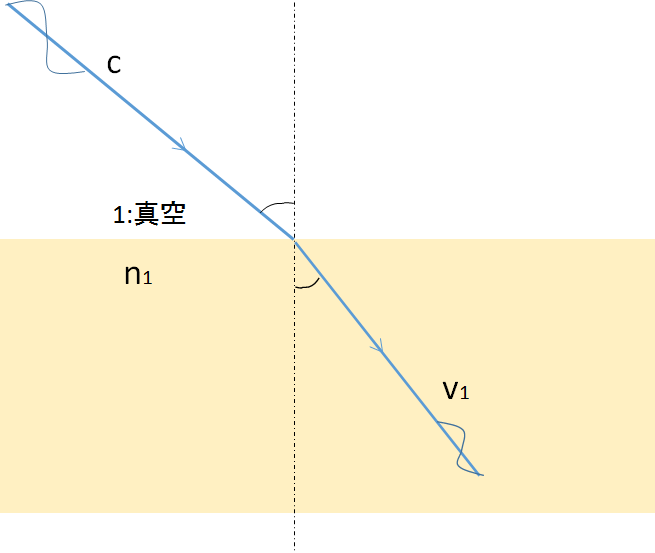
次の図を見てください。($c$ は光速)
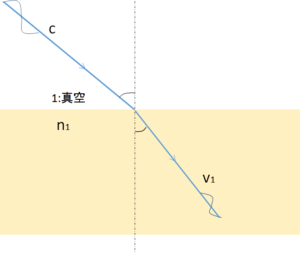
したがって、
\begin{eqnarray}
n_{1}&=&\dfrac{c}{v_1} \\
\end{eqnarray}
もう一つありますね。
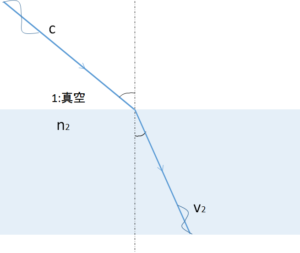
\begin{eqnarray}
n_{2}&=&\dfrac{c}{v_2} \\
\end{eqnarray}
です。これら2つの式から
\begin{eqnarray}
v_{1}&=&\dfrac{c}{n_1} \\
\\
v_{2}&=&\dfrac{c}{n_2} \\
\end{eqnarray}
ですね。これらを代入します。
\begin{eqnarray}
n_{12}&=&\dfrac{v_1}{v_2}\\
\\
&=&\dfrac{\dfrac{c}{n_1}}{\dfrac{c}{n_2}}\\
\\
&=&\dfrac{n_2}{n_1}\\
\end{eqnarray}
そうすると、
\begin{eqnarray}
\dfrac{\sin \theta _1}{\sin \theta _2} &=&\dfrac{n_2}{n_1}\\
\end{eqnarray}
ゆえに、
$$n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 $$
となることがわかります。
この式を使いましょう。
ちなみに、屈折率が入れば他にも同じ式が使えます。
$$n_1 \times v_1 = n_2 \times v_2 $$
$$n_1 \times \lambda_1 = n_2 \times \lambda_2 $$
注意ですが、以下は間違いです。
$$v_1 \times \lambda_1 \neq v_2 \times \lambda_2 $$
同じノリでやってしまいがちなので注意してください。
多層構造の場合
違う種類の物質が幾重にも重なっている場合です。
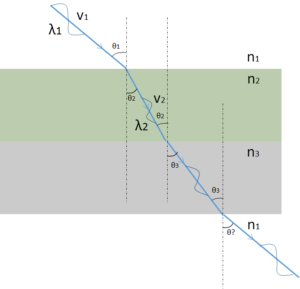
次のことが言えます(ここ重要)
\begin{eqnarray}
n_1 \times \sin \theta_1 &=& n_2 \times \sin \theta_2 \\
&=&n_3 \times \sin \theta_3\\
&=&n_1 \times \sin \theta_?\\
\end{eqnarray}
ここで当然ですが式から、 $\sin \theta_? = \sin \theta_1$ ですね!
したがって、$\theta_? = \theta_1$ となることがわかります。
このように何層続いてもいいので(途中で全反射しない限り)、次のことが言えます。
この式を使えば、いままで頭を悩ましてきた問題がすんなり解けるはずです。
\begin{eqnarray}
n_1 \times \sin \theta_1 &=& n_2 \times \sin \theta_2 \\
&=&n_3 \times \sin \theta_3\\
・\\
・\\
&=&n_{100} \times \sin \theta_{100}\\
\end{eqnarray}
重要な注意点:単純にこの式が成り立つのは物質が平行に重なっているときだけです。
今まで、光の進入方向が逆の場合に割り算の分子と分母を間違える人をたくさん見てきました。
しかし、掛け算で行えば考えることなく、気楽に立式できます。
重要なことは、割り算は順序(割る順番)を間違えると致命傷ですが、掛け算では答えに影響しないということなのです。
全反射にも応用
全反射という現象がありますが、この公式をそれこそ「呪文」のように覚えている人を見かけます。
しかし、全反射の式というものは全く覚える必要がないものです。
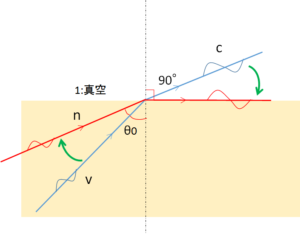
図の赤いラインが全反射する前の臨界です。
このときの角度 $\sin \theta_0$ を臨界角といいます。
ここで、真空の屈折率が 1 ですから、先程の掛け算による屈折の式を使って、
$$ 1 \times \sin 90 ^ \circ =n \times \sin \theta_0 $$
は当然と言えますね。これがいわゆる全反射の式です。
これだけです。
ひとつ、全反射の式に物理的な意味を見出すとすれば絶対屈折率の逆数が臨界角 $\theta_0$ の $\sin$ となることです。
真空ではないときは真空の屈折率 $1$ の代わりに、その物質の屈折率 $n’$ を使えばいいだけです。
$$n’ \times \sin 90 ^ \circ =n \times \sin \theta_0 $$
$$\sin \theta_0 = \dfrac{n’}{n}$$
このとき $\sin\theta_0 \leqq 1$ ですから、全反射が起こるときは必ず、$n >n’ $ です。($=$ のときは屈折しません)
つまり、屈折率の大きい物質から小さい物質へ抜けるときだけ全反射がおこります。
まとめ
掛け算による式
$$n_1 \times \sin \theta_1 = n_2 \times \sin \theta_2 $$
を使うことでミスを防げるだけでなく、時間短縮も期待できます。
ぜひお試しください。
こちらの記事も参考に!ドラゴン桜と学ぶ学習メディア スネルの法則





































コメント