X線
X線は電磁波の一種で、紫外線よりもさらに短波長(高周波数・高エネルギー)側に位置しています。

- 電磁波
- 強力な透過力(高エネルギー)
- X線の最大エネルギー $E=eV=h\nu_0=\dfrac{hc}{\lambda_0}$
$e$:電子電気量 $V$:加速電圧 $h$:プランク定数 $c$:光速
$\nu_0$:最大振動数 $\lambda_0$:最短波長
X線は、19世紀末に発見されたナゾの放射線・・・X線、と名付けられたのですが、当時の医療診断に絶大な貢献をしたことはいうまでもありません。レントゲン線ともいいます。
なんといっても、X線の透過作用を利用すれば、人体を切開せずに体の内部を知ることができるのです。医療に大いに役に立ったことでしょう。
発見者のレントゲン(Wilhelm Conrad Röntgen 1845-1923 )の第1回ノーベル賞受賞(1901年)は当然のことといえます。
X線の発生

$e$:電子電気量 $V$:加速電圧 $h$:プランク定数 $c$:光速
$\nu_0$:最大振動数 $\lambda_0$:最短波長

レントゲンは陰極線の実験をしていてX線の存在に気がついたようですが、X線の発生に良く用いられるのが図のクーリッジ管です。
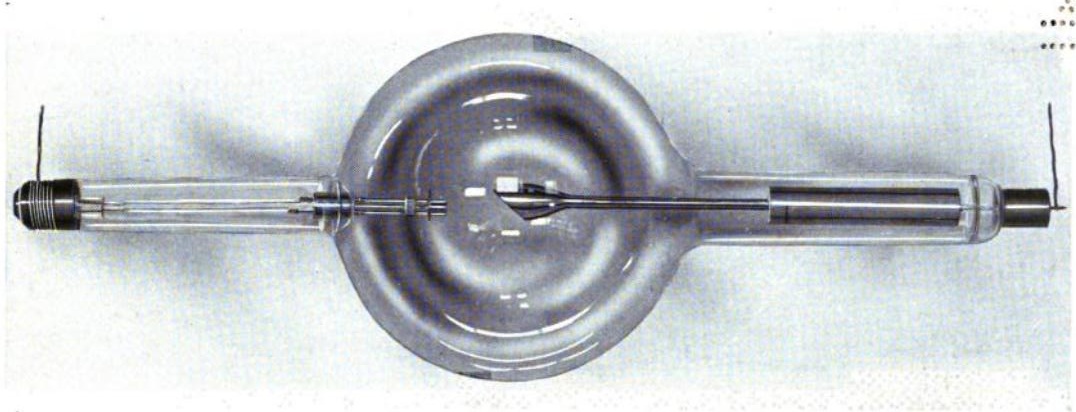
https://commons.wikimedia.org/wiki/File:Coolidge_xray_tube.jpg#/media/ファイル:Coolidge_xray_tube.jpg
真空にしたガラス管(クーリッジ管)に金属の電極(ターゲット)を封入します。フィラメントから放出された電子(熱電子)を陽-陰極間で加速して陽極(ターゲット)に衝突させます。その際、加速された電子のエネルギーがX線に変換されます。
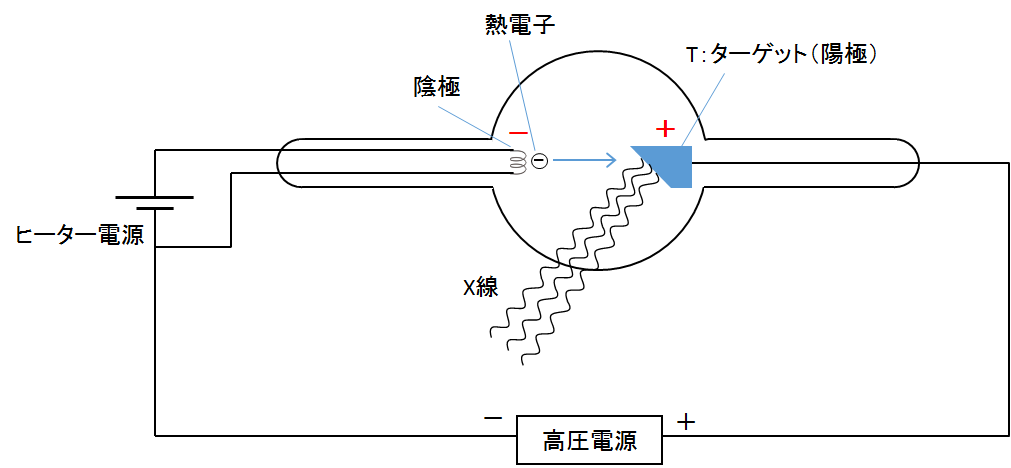
このとき、電子(電荷 $e$ )の加速によって得られたエネルギー全てをX線(最大振動数 $ \nu_0 $)のエネルギー $E=h\nu_0$ に変換したとします。( プランク定数 $h$ 加速電圧 $V$ 光速 $c$ )
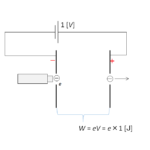
そうすると、電子の運動エネルギーが最初 0 だったとして、エネルギーの原理($E_0+W=E$)から
$E_0+W=E$ $E=h \nu$ 、 $W=qV=eV $より、
$0 + eV = h\nu_0$
$\nu_0=\dfrac{eV}{h}$
電圧 $V$ ではこれ以上の振動数のX線は生じません。
そのときの波長が最短波長で $\lambda_0$ とすると、
$c=\nu_0\lambda_0$ だから
$\lambda_0=\dfrac{hc}{eV}$
電圧 $V$ ではこれ以下の波長のX線は生じません。加速電圧によって最短波長・最大振動数は決まります。
連続X線と固有X線
図は、X線波長とその強度の関係を示しています。
X線は一般に、連続X線と固有X線とに分けることができます。
- 連続X線 ・・・ 波長が短いほうから長いほうへ連続的に滑らかに伸びている
最短波長は加速電圧によりきまります。 - 固有X線 ・・・ 特定の波長(特定のエネルギー)で大きな強度を持つ
固有X線はターゲット(陽極)の材質によりその波長が決まっており、加速電圧によりません。
図では、加速電圧を変えたときのX線スペクトルにおいて、固有X線はいつも同じ波長(エネルギー)のところにあることを示しています。
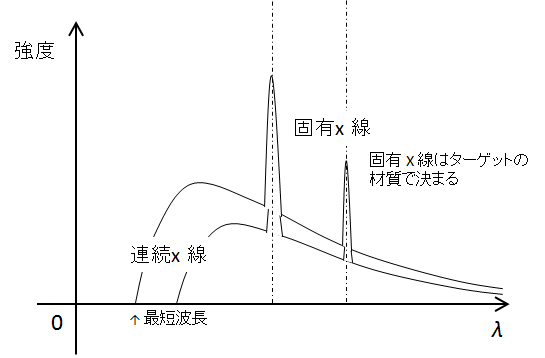
これは以下のように説明されます。
連続X線
加速する荷電粒子は光子を放出します。
これを利用しているのが、放射光施設(SPring-8など)です。
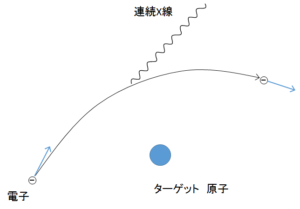
電子がターゲットに近づくとターゲットの原子と相互作用して加速運動(進路が曲げられるなど)します。
そのさいに、エネルギーをX線として放出しているのです。
このとき電子の軌道は自由に取ることができます。したがって、その進路が曲げられるなどして放出されるX線のエネルギーは連続的な値を取ります。
固有X線
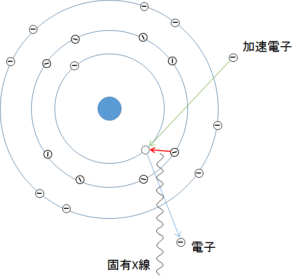
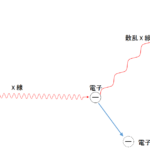
固有X線は、加速された電子がターゲットの原子の内殻電子を弾き飛ばすことにより生じます。
弾き飛ばされて空いた内核には、より高いエネルギーを持つ外側の電子が落ち込むため、あまったエネルギーをX線として放射します。
電子の軌道でのエネルギーは決まっています。つまり、ある電子殻からある電子殻まで電子が遷移した場合、その電子殻同士では、放出されるエネルギーはいつも同じになります。
よって、特定のエネルギー(波長)のX線が常に強く放射されることになります。
したがって、固有X線の波長(エネルギー)は、電子の加速電圧によらずいつも一定になります。
また、固有X線の波長はターゲットの材質で決まります。
例として、
図のL殻からK殻へ落ちるときのエネルギーはいつも同じなため、常に同じ波長のX線が放出されます。
(他の殻から落ち込むときは違うエネルギーを放出するため、固有X線は同じターゲットでも通常、いくつか存在します)
X線の波動性
先に述べたように、X線は波長の短い電磁波の一種です。
ゆえに、電磁波としての性質として波動性を持ちます(X線光子として粒子性もあわせもっています)。
つまり、波動性の特長として、回折・干渉現象を示すはずです。
可視光の波長に比べるとX線の波長は非常に短い( $\frac{1}{1000}$ 程度以下 )ため、光学実験で使用した回折格子などでは格子間隔が広すぎて、回折・干渉現象の観測が困難です。
そのため、結晶格子を回折格子とすることで回折・干渉が観測できることが予言され、後に実験で撮影されています。
図は単結晶によるラウエ斑点と呼ばれるX線回折像です。

phys.sci.hokudai.ac.jp/LABS/kyokutei/vlt/research/XRD.htm
ブラッグの条件
www.toray-research.co.jp/technical-info/analysis/structure/str_006.html
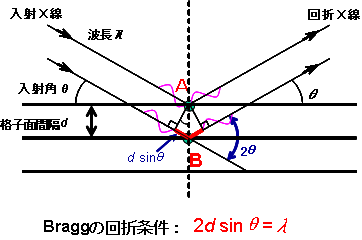
一般に結晶間隔は非常に狭く、入射X線は平行とみなせます。
図の2つのX線が結晶( 面間隔 $d$ )で反射されるとき、その光路差は $2d\sin \theta$ 。
X線の波長を $\lambda$ とするとき、
$2d\sin \theta =n \lambda$ $(\: n=1,2,3,\:\cdots \:)$
これをブラッグの条件と呼びます。この式はX線結晶学上、重要な式です。
この式を満たすとき、2つのX線は同位相となるため強めあい、スクリーン上に像を結ぶことになります。
先に述べた固有X線など、その波長が良くわかっているX線を使えば、ブラッグの条件の式により、面間隔 $d$ 値を計算でき、結晶の構造解析に役立てることができるのです。
その他、試料として結晶を良くすりつぶした粉末を用いると、回折像が円形に広がるデバイシェラー環(デバイシェラーリング)を得ます。
結晶を良くすりつぶすと、単結晶とは違い、小さい小さい結晶が粉末試料中にあらゆる方向を向いて存在することになります。
そのため、X線ビームが通る粉末試料中に、上述のブラッグの式を満たす結晶が必ず存在します。
それにより、X線回折像が円形状に放射されるのです。
図は粉末試料のX線回折像です。
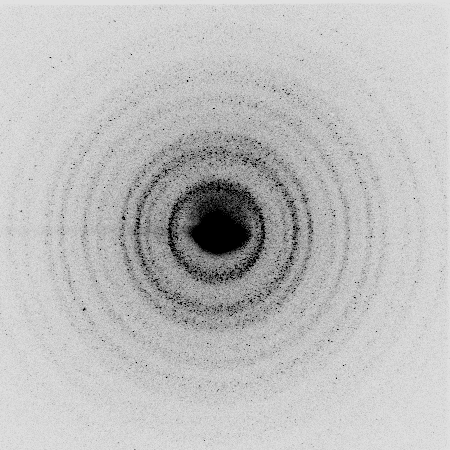
デバイシェラー環 デバイシェラーリング




































コメント