熱力学第2法則
熱力学第2法則とはどのようなものでしょうか?
熱力学第2法則を表現したものとして、これから述べる「クラウジウスの原理」と「トムソンの原理」が知られています。
熱力学第1法則はこちらへ
クラウジウスの原理

「熱は高温の物体から低温の物体へ移動し、自然に低温の物体から高温の物体へ移動することはない」クラウジウス(1822~1888)
クラウジウスの原理は、物理学ではおなじみの、「数式の嵐」が出てくるわけでもなく、誰にもわかる平易な言葉で示されています。
このクラウジウスの原理は、例えば、
お湯を入れたコップを放置すれば熱は周囲に逃げていき、コップのお湯はやがて冷める。
そして、逃げていった熱はひとりでには戻ることはない。
つまりコップの水は外部から何らかの作用を受けない限り冷めたままである。
と言っているのですね。
なんだか当たり前のことを言っているような気がしませんか?

これが物理の法則なのか?
熱力学の法則とはこの程度のものなのか・・・
と思われる人も見えるかもしれません。
上にあげたような、一方向だけの変化を不可逆変化といいます。
ではその逆は、例えば、
「冷えたコップの水を放置すれば、逃げていった熱が集まりコップの水が再び熱くなる」
です。これは常識的に考えてもあり得ないし、見たこともありません。
逆もまた可能であるというような変化としては、
例えば、真空中で振り子を降らせると、空気抵抗がないのでいつまでも振れ続ける
のようなものがあります。
こういう変化を可逆変化といいます。
一般に熱の出入りを伴う変化は不可逆です。
(世の中の現象は、ほぼ摩擦を伴うので、普通は熱の出入りを伴います)
当時の科学者たちは、熱現象がなぜ不可逆なのか?
なぜ熱は自然には温度の高いところから低いところへしか流れないのか?
について、物理的な説明を与えるべく試行錯誤したそうですが、だれも成功しなかったのです。

このような問を持ち、考える
というのが凡人ではない証拠かも
そのため、、クラウジウスはなぜ? と問うことをやめ、それを物理学の原理として土台に据えることにしたのです。

物理学上の原理とは、今の所、なぜかという問には答えるのは難しいものの、経験上、自然における根本的な仕組みであると考えられるものです。
トムソンの原理
さて、トムソンの原理を見てみましょう。
トムソンの原理の発見の背景には、当時の産業革命が大きく影響しています。
つまり、機械に、少ない燃料で多くの仕事をさせる・・という産業界からの要望があったのです。
(当時、初期の熱機関効率は非常に悪いものだったらしいです)
ところが、経験上、与えたエネルギーをすべて仕事に変えることはできないらしい・・・ということがわかってきました。
そこで生まれたのが
トムソンの原理
「まわりになんの変化も残すことなく、吸収した熱をすべて仕事に変えることはできない。」
トムソン(1824-1907)
これはクラウジウスの原理と同等であることがわかっています。
さらに「第2種永久機関は存在しない」「熱効率100%の機械は存在しない」というのも熱力学第2法則の別表現です。
興味深いことには、これらの原理は「~~~ない」という否定表現であることです。
これは物理の法則・原理としては珍しいですね。
他に、「エントロピーは増大する」とも表現されます。
エントロピー
さて、このように熱力学研究が行われていたのですが、その過程でエントロピーという物理量が発見されます。
エントロピー
「断熱過程において、移動した熱量 $\Delta Q$ とその時の物体の絶対温度 $T$ について、$\dfrac{\Delta Q}{T}$ を考えてエントロピーと名付ける。一般に、閉じた系のエントロピーは増大する」
もう少しくだけていえば、
「移動した熱量 $\Delta Q$ を絶対温度 $T$ で割ったもの $\dfrac{\Delta Q}{T}$ をエントロピーと名付ける。高温物体(温度 $T_H$ )と低温物体(温度 $T_L$ )という2つ以上の物体の間だけで熱が移動するとした場合、そのエントロピーの総量は増大する」
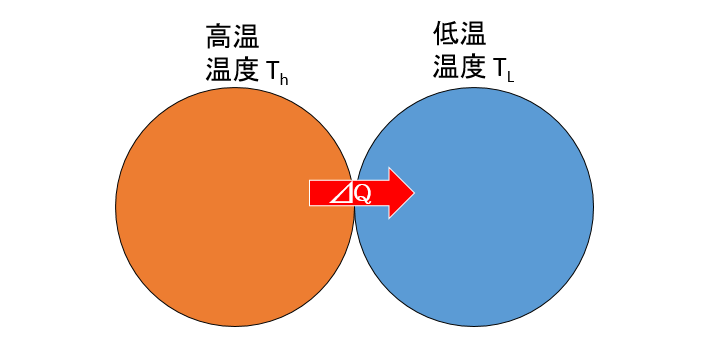
今、2つの物体があり、接触しているとしましょう。(熱は2物体間のみで移動するものとします)
そのとき、高温の物体(温度 $T_H$ )から低温の物体(温度 $T_L$ )へ、ごく小さい熱 $\Delta Q$ が移動したとします。
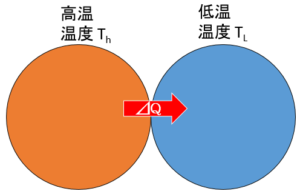
では、先ほど述べた定義に従ってエントロピーの計算をしてみると、
高温部のエントロピー・・・$\dfrac{-\Delta Q}{T_H}$
低音部のエントロピー・・・$\dfrac{+\Delta Q}{T_L}$
となります。高温部のエントロピーに $-$ の符号がついているのは、高温部から熱が流出したからです。
さて、これら2つの物体でのエントロピー総和を考えます。
そうすると、
$$\dfrac{-\Delta Q}{T_H}+\dfrac{+\Delta Q}{T_L} $$
となります。
この場合、$T_H > T_L$ であることは当然でしょう。
ということは、
\begin{eqnarray}
\dfrac{-\Delta Q}{T_H}+\dfrac{+\Delta Q}{T_L} &=& \Delta Q \left( \dfrac{-1}{T_H}+\dfrac{1}{T_L}\right)\\\\
&=& \Delta Q \left( \dfrac{T_H-T_L}{T_H \cdot T_L}\right)>0\\\\
\end{eqnarray}
です。つまり、温度変化がある場合は、エントロピーの総和は必ず正になることがわかります。
クラウジウスの原理(熱はかならず温度の高いほうから低いほうへ流れる)が正しいとすれば、このように他との熱のやり取りがない(閉じた系)で、それらのエントロピー総和は増大する方向に現象は進みます。
これがエントロピー増大の法則です。
いろいろな現象が起きたとしても、エネルギー保存則である「熱力学第1法則」から、そのエネルギー総量は変わることなく形を変えるだけです。
しかし、エントロピーは現象を経るごとに、確実にその量が増大していくことになります。
例えば、ガソリンを燃やして車を走らせるとき、ガソリンの持つ化学エネルギーを運動エネルギーと熱エネルギーに変えます(このとき熱効率は決して100%にはなりません)。
エネルギーはその形態を変えました。エネルギーの総量は不変ですが、エントロピーは増大します。
そして、最終的には車は停止し、その持っていた運動エネルギーを熱エネルギーとして捨てることになります。
そして、さらにエントロピーは増大します。
最終的には、あらゆるエネルギーは熱エネルギーとなります。
(注:エネルギー総和は変化していません)
しかし、拡散した熱エネルギーを再利用するのは難しく、とても使いにくいエネルギーです。
これを「乱雑さが増した」と表現しているのです。




































コメント