いまさら聞けない　スリット間隔

いまさら聞けない　スリット間隔の疑問

スリットの間隔

スリットの本数が 1 cmあたり8本のとき、スリット間隔はいくらになるのか？

だれしもちょっと？となったことがあるかもしれません。

えーと、図を描いてみると････

このようにスリットを並べると間隔は7つあるから、スリット間隔は

$\dfrac{1}{7}=0.142857\:\cdots\:\mathrm{cm}$

ですね？

ちょっと待った！

それでは 1 cmあたり7本しか入っていません。

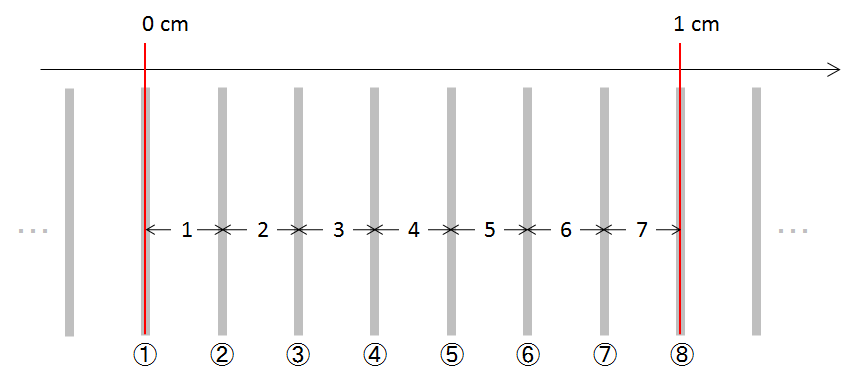
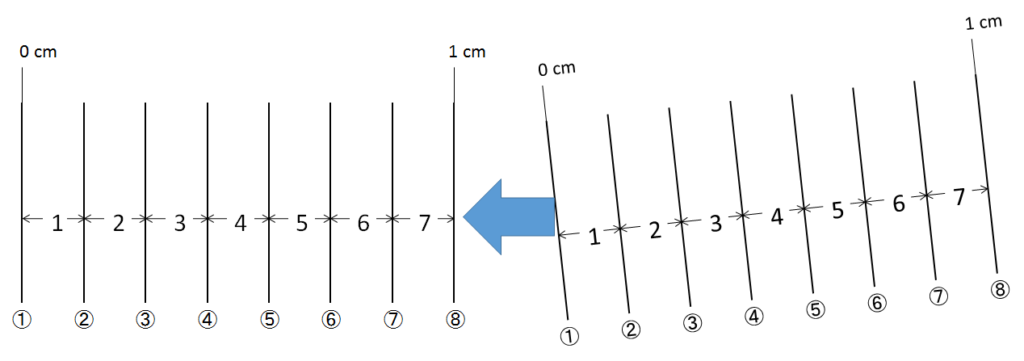
スリットが完全に 0 ～ 1 cmの中に入るようにすればわかりやすいかもしれません。次の図を見てください。

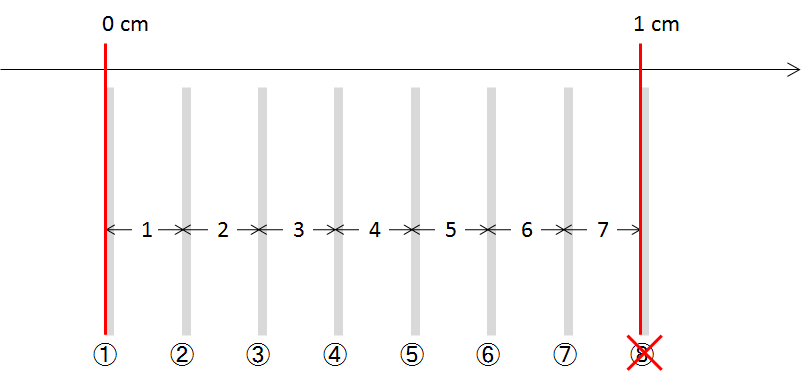
右端の⑧番スリットは 0 ～ 1 cmの外であることに注意してください。

これを見ると 1 cmの間にスリットが7本しか入っていないことが明瞭ですね！

では、1 cmの間にスリットを8本入れるとどうなるでしょうか？

次の図では 1 cm間隔にスリットを8本入れました。少し窮屈になりましたね。

そうすると、 0 ～ 1 cmの間にスリット間隔は8つあることがわかると思います。

よってスリット間隔は

$\dfrac{1}{8}=0.125\:\:\mathrm{cm}$

となります。

スリット間隔というのはスリットの中心間の距離 $d$ だと考えればよいでしょう。

スリットが幅のない線だったら？

それって、スリットに幅があるからですか？

いえ、数学の線のように幅がない場合も同じです。

例えば、線分がたくさんある状況を考えて、線分が7本入る、幅が 1 cmの枠を考えてください。

この枠をどのように動かしても、枠内に線分が7本入るという状況は変わらないはずです。

したがって、次のような場合も7本だと考えなければなりません。

幅 1 cmの枠に8本入る場合は次のような図になります。

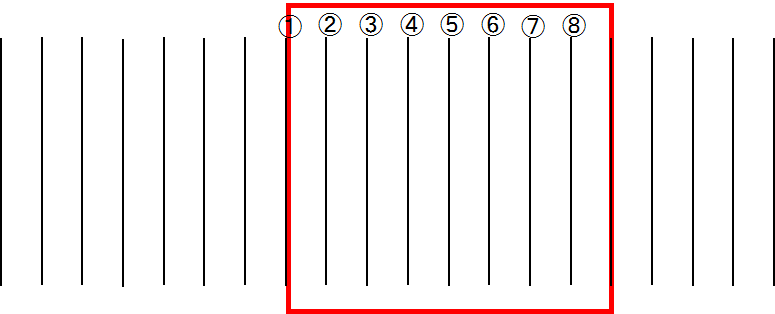
よって、この場合も、線の間隔は、

$\dfrac{1}{8}=0.125\:\:\mathrm{cm}$

です。

あるいは、

例えば、1 cmの幅に線分が8本あるとします。

このようなイメージになるかもしれませんが、もしこれを１セットとして数えてしまうと、おかしなことになります。

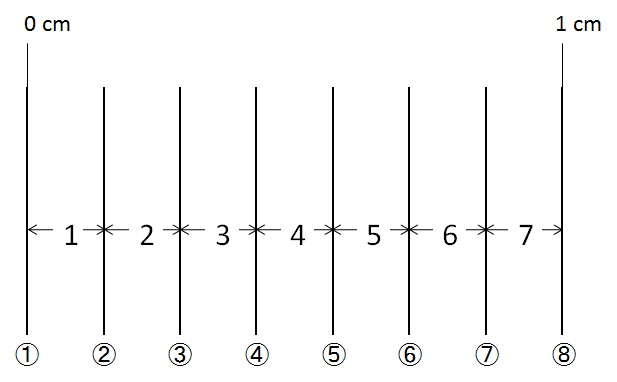
次の１セットをつなげてみましょう。

そうですね。⑧番目の線分が右の①番目の線分と二重になってしまいます。

だから、次のように考えるべきですね。

このセットをつなげると

となって連続します。