物理のエッセンス 力学30番
P.30 の Ex.2 の問題を少し変化させます。
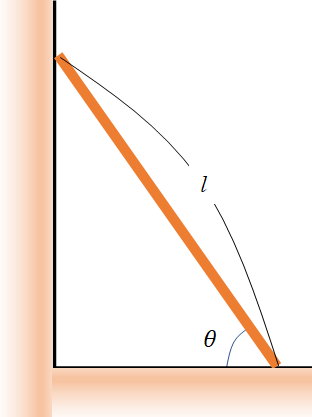
図で、角度 $\theta$ を徐々に小さくしていくときの、棒が滑り出す角度 $\theta_0$ について $\tan\theta_0$ を求めます。
Ex.2と違ってこちらは壁と棒にも摩擦があります。
棒と壁の間の静止摩擦係数が $\mu ^{\prime}$ 棒と床の間の静止摩擦係数を $\mu$
(棒の長さ $l$ 、棒の質量 $m$)
解法


念のため、ここでもう一度、おさらいしておきましょう。
基本的に剛体の問題の解き方は決まっています。
それは
- 図を描いて、注目物体にはたらく力をすべてかき入れる。← 最重要
- 力のつりあいの式をたてる
- ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
- 以上の式を連立する
です。
多少の違いはあります(手順2・3などの一部が不要なこともあります)が、基本的にはこのようにすればほとんどの問題の糸口はつかめるはずです。
1. 図を描いて、注目物体にはたらく力をすべてかき入れる。
注目物体が受ける力をすべてかき込みましょう。
題意に従って、棒が滑り出す直前を考えます。

ここで、棒と壁、棒と床の静止摩擦係数が違うけどいいの?
と思われるかもしれません。結論としては気にする必要はありません。
角度 $\theta_0$ を小さくしていって、棒の端のどちらか片方が先に最大摩擦力を迎えても、他が支えています。
そのため、結局滑り出す直前には両端ともに、最大摩擦力であると考えられます。
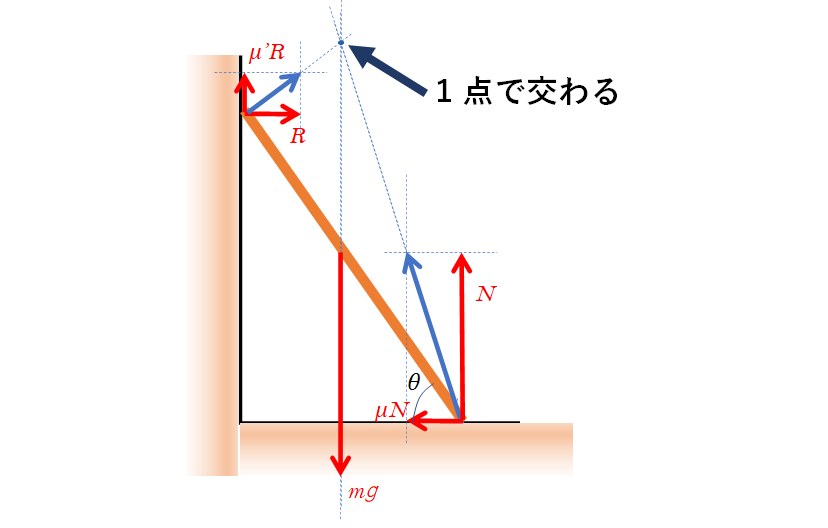
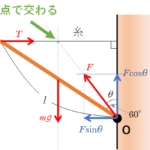
ここでは棒に注目しているので、次のような図になります。
($R$、$N$ :垂直抗力 $mg$ : 重力)
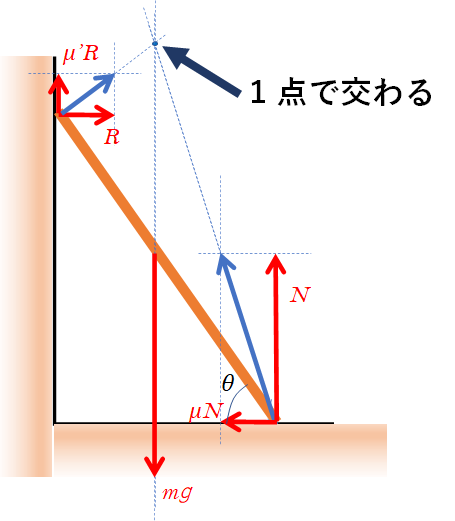

壁と棒の間にはたらく静止摩擦力 $\mu^{\prime}R$ の方向ですが、ここで迷う人もいるのでは?
この問題の場合、図のようにすべての力は1点で交わるため、棒と壁の間には鉛直上向きに摩擦力がはたらきます。
2. 力のつりあいの式をたてる
鉛直方向
$mg=\mu^{\prime} R + N \: \: \cdots \cdots \: 1$
水平方向
$R=\mu N \: \: \cdots \cdots \: 2$
3. ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
Aまわりモーメントを考えます。

なるべく計算が楽になりそうなところを探しましょう。
また、棒は一様であると考えて、重心は棒の中央にあるとします。
したがって、重力のAまわりモーメントは $mg\dfrac{l}{2}\cos \theta$ です。
以上のことを踏まえて式をたてましょう。
$mg\dfrac{l}{2}\cos \theta + \mu N l \sin \theta =Nl \cos \theta \: \: \cdots \cdots \: 3$
4. 以上の式を連立する
式 1 と 2 から $R$ を消去して、
$mg=\mu^{\prime} (\mu N) + N$
$~~~~~=N(\mu \mu^{\prime} + 1)$
よって、
$N=\dfrac{mg}{\mu \mu^{\prime} + 1}$
式 3 の両辺を $\cos\theta $ で割って( $\theta <90^{\circ}$ なので $\cos\theta > 0$ です)、 $\tan \theta $ を作ります。
$mg\dfrac{l}{2}\cos \theta + \mu N l \sin \theta =Nl \cos \theta \: \: \cdots \cdots \: 3$
$\times \dfrac{1}{\cos\theta}$ して
$mg\dfrac{l}{2} + \mu N l \tan \theta =Nl $
$\tan\theta = \dfrac{Nl – mg\dfrac{l}{2} }{\mu N l}$
ここへ先ほどの $N=\dfrac{mg}{\mu \mu^{\prime} + 1}$ を代入して答えを得ます。
$\tan\theta = \dfrac{Nl – mg\dfrac{l}{2} }{\mu N l}$
$~~~~~~~~~= \dfrac{\left ( \dfrac{mg}{\mu \mu^{\prime} + 1}\right ) l – mg\dfrac{l}{2} }{\mu \left (\dfrac{mg}{\mu \mu^{\prime} + 1} \right ) l}$
$~~~~~~~~~= \dfrac{\left (\dfrac{1}{\mu \mu^{\prime} + 1} \right ) – \dfrac{1}{2} }{\mu \left (\dfrac{1}{\mu \mu^{\prime} + 1} \right ) }$
整理して
$\tan\theta = \dfrac{1-\mu\mu^{\prime}}{2\mu}$
動画で解説
上記の説明と記号が少し異なります。




































コメント