電位とは何か？電位の基礎を超やさしく徹底解説

さて、電場、電気力線と学習は進みましたか？
それではいよいよ電位について考えていきましょう。

この記事では電位と電場の違いについて詳しく解説します。
この記事を読むことで、電場と電位について明確にイメージできるようになるはずです。

電位とは何か？電位の基礎を徹底解説

電位とは簡単に言ってなにか・・・？
V (ボルト) のことです。
ではどうもなんだかよくわかりませんね・・

もっとわかりやすく言えば仕事・エネルギーのことです。
エネルギーですから、スカラーであり、方向性はありません。
これは電場がベクトル量であり方向性を持つことと大きく違います。

それでは、電位についてやさしく説明していきましょう！

電位は電気の世界の仕事・エネルギー　力学的な考え方と同じ

電位は電気の世界の仕事・エネルギーです。

基本的な考え方は、力学的な考え方と同じです。だから、物理のキモは力学にあると言えるのです。ここでは重力による位置エネルギーと対比してみましょう。

位置のエネルギー $U$ を覚えていますね。
重力による位置エネルギーは、重力加速度 $g$ で、基準面より高さ $h$ のところにある質量 $m$ の物体が持つエネルギーで、$U=mgh$ と示されます。

注意すべき点は、この位置のエネルギーの基準面はどこにとってもよいことです。
基準面のとり方によっては位置エネルギーは正になったり、0になったり負になることもあります。

この重力による位置エネルギーは仕事との関係から導くことができました。
基準面から重力に逆らってゆっくりと物体を高さ $h$ だけ引き上げる仕事 $W$ を求めてみましょう。

重力は $mg$ ですから、物体を引き上げるための力 $F$ は $F=mg$ であればOKです。
仕事は、力 × 距離 で示されますから、高さ $h$ だけ引き上げる仕事 $W$ は、

$W=F\times x =mg\times h$

と表すことができます。

したがって、基準面から高さ $h$ の位置にある質量 $m$ の物体が持つ位置エネルギーはこの仕事がエネルギーに変換されたと考えて $mgh$ で示されます。

---

電気の世界における仕事を考えることで電気の世界の位置エネルギー $U$ を定義します。
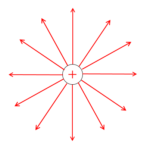
例えば図のように、$＋q\:[\mathrm{c}]$ の電荷があるときを考えます。
$＋q\:[\mathrm{c}]$ の電荷をその受ける力に逆らって運ぶときにも当然仕事が必要ですから、重力の場合と同じように位置のエネルギーを考えることができます。

 

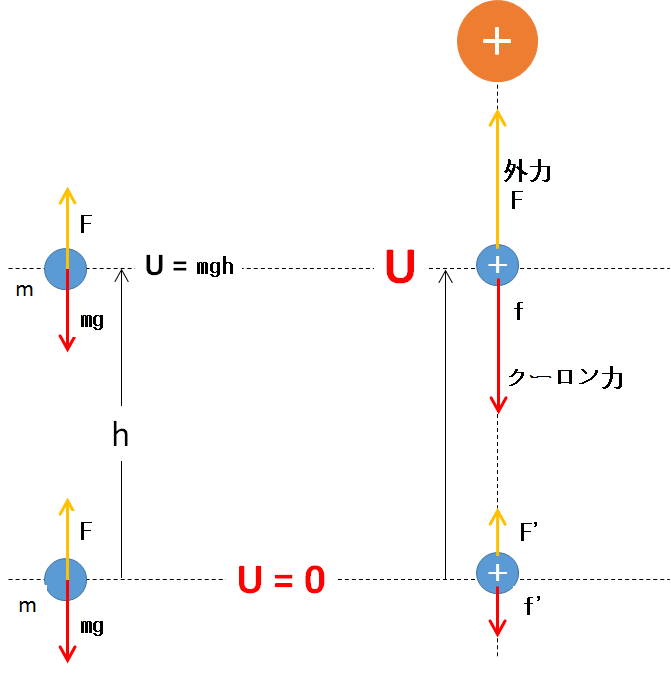
では電位とは何かというと、この位置エネルギー $U$ を $1\:[\mathrm{c}]$ 当たりの量にしたものなのです。
その地点で $1\:[\mathrm{c}]$ の電荷が持つ位置エネルギーを電位というのです。

つまり、電位とは電気的な位置エネルギー $U$ として、 $\dfrac{U}{q}$ で示されます。
これで $1\:[\mathrm{c}]$ あたりのエネルギーになりますね。
よって、ここで電位を $V$ で示すことにすると、

$V=\dfrac{U}{q}$

ということになります。
注意してほしいのは電位を $1\:[\mathrm{c}]$ 当たりの位置エネルギーと定義している点です。
電位とは $1\:[\mathrm{c}]$ について考えればよいというわけですね。

もし、重力の場合に同じような物理量を考えるとすれば、$1\:[\mathrm{kg}]$ あたりの位置エネルギーとなり、重位？・・ $gh$ のような式で表されます。実際にはそのような量は考えませんが・・・。

電場との違い

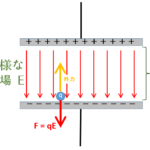
電場を思い出しましょう。
電場とは空間の電気的な歪みでした。
具体的に言えば、$+1\:[\mathrm{c}]$ の試験電荷が受ける力で示されるものです。
力で示されるので電場はベクトルです。一方、電位は仕事やエネルギーのイメージなのでこちらはスカラーなのです。

イメージでわかる電場の基礎

電場とはどのようなものか？ いままでしっくりこなかったあなたに、たとえ話で解説します。 これで電場のイメージはばっちりです。

kokolainen.com

そして電気力線とはその歪みを表すために導入されたイメージです。

イメージを作ろう　電場と電気力線

電気力線に悩む人は多いようですが、これをきちんと理解して使いこなせれば鬼に金棒です。いろいろなところで役に立ちます。 さらに逆二乗則についても解説。 コンデンサーと電場、電気力線との関係も詳しく解説しています。

kokolainen.com

電位の基準点

先ほどお話したように、電位は $1\:[\mathrm{c}]$ 当たりの位置エネルギーと定義されていますから、当然、重力の位置エネルギーの場合と同じく、そのエネルギーの基準面（点）が必要です。

重力による位置エネルギーの基準は自由にとることができました。
そのため、位置エネルギーが正になったり負になったり0になったり、同じ位置にある物体の位置エネルギーであっても基準面のとり方により、いろいろと変化しました。

電位の場合でも理論的にはどこをエネルギーの基準に取ろうが自由です。
しかし、利便性を考えて電位の基準は、一般には無限遠を基準に決めます。

ここで無限遠と言うと、それだけで「はぁ」とため息が出そうですが、いえ、そんなに難しいことではありません。

重力の世界でも基準を無限遠にとることは普通にやっていることです。
例えば、万有引力による位置エネルギー基準には無限遠を取りますよね。
万有引力を示す式を見ると、万有引力 $f$ は距離 $r$ の2乗に反比例しています。

$f=G\dfrac{mM}{r^2}$

すなわち、$r \rightarrow \infty $ としたときに万有引力が 0 になります。

同様に、電気の場合でもクーロン力は次の式で示されますから

$f=k\dfrac{qQ}{r^2}$

無限遠 $r \rightarrow \infty $ としたときに力 $f$ や電場 $E$ の大きさは 0 になります。

このように計算上 0 になるような点を基準に設けると都合が良いのです。
なぜかって？片側が常に 0 ですから計算の手間が省けますよね。

電位をイメージ

もっと具体的に言いましょう。
ある点の電位は $+1\:[\mathrm{c}]$ を無限の彼方からその点まで運ぶ仕事で示されます。
このとき、電場の原因となっている電荷 $Q$ が正でも負でもかまいません。

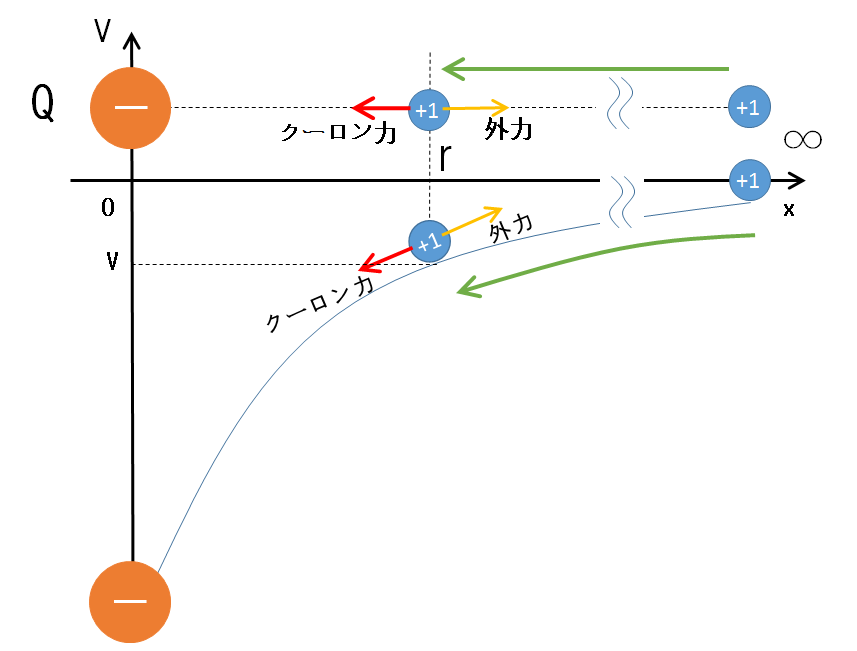
例えば、電荷 $Q$ が正のときは次の図のように、 $+1\:[\mathrm{c}]$ には反発力であるクーロン力がかかりますから、無限の彼方から距離 $r$ の所まで運ぶときの外力のする仕事は正です。ゆえに電位も正となります。

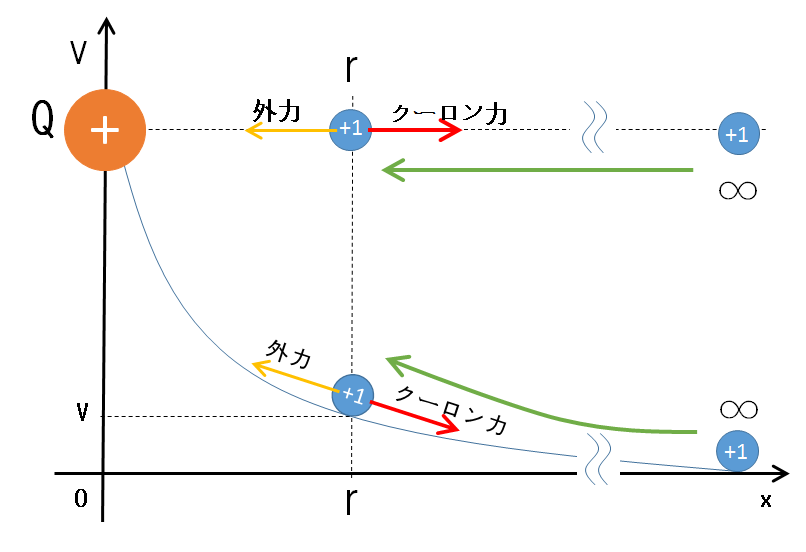
それでは、電荷 $Q$ が負であるなら次の図のようになり、 $+1\:[\mathrm{c}]$ には引力のクーロン力がかかります。
このクーロン力に逆らって無限の彼方からゆっくりと $+1\:[\mathrm{c}]$ の電荷を移動させる仕事を考えます。
このとき、無限の彼方から距離 $r$ の所まで運ぶときの外力のする仕事は負です。ゆえに電位も負となるのです。なぜ負になるか？—> 外力の働く向きと運動向きが正反対だからです。

無限の彼方からなら無限の時間がかかるのでは？と思う必要はありません。

仕事は、$W=F\times x$ なので時間には無関係だからです。
一瞬で移動しようが100万年かかろうが仕事量は同じです。
だから実際にそれが可能かどうかはさておいて、定義上は有効なのです。

まあ、電場から受ける力の大きさは距離の2乗に反比例するので、実際上はそれほど遠くへ行かなくても $0$ とみなせます。

---

では電荷 $Q$ から $r$ だけ離れた点の電位 $V$ を求めてみましょう。

$+1\:[c\:]$ の電荷を、無限遠から $r$ の点まで運ぶときに外力のする仕事がその点の電位となりますから、このときの仕事 $W$ を求めます。
そこで力学で学習した仕事の定義、

$W=Fx$

より、力 $F$ と移動距離 $x$ がわかれば良いように思いますが、この式は単純に $F$ が一定の場合しか成り立ちません。

クーロン力 $f$ は

$f=k\dfrac{q Q}{r^2}$

でわかるように一定では無いので単純に $W=Fx$ の式を使うことはできません。

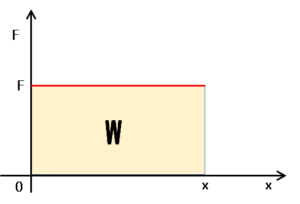
クーロン力をグラフを示すと次のようになります。
先程のグラフでも面積が仕事になりました。
したがって、この場合の仕事は図の面積を求めれば良いことになるのです。

ここでは電位を求めているので $+1\:[\mathrm{c}]$ についてのクーロン力（電場ですね）について考えます。
そこで、$f=k\dfrac{1\times Q}{x^2}$のグラフを次に示します。

この $r$ から $\infty$ までの面積は積分を利用して求めましょう。
かかる力は、 電荷 $+1\:[\mathrm{c}]$ についてですから、距離 $x$では $f=k\dfrac{1\times Q}{x^2}$ です。
よって、横軸を $x$ として、

$$W=\int_r^{\infty} k\dfrac{1\times Q}{x^2}dx$$

ですね。

すなわち、

\begin{eqnarray}
W&=&\int_r^{\infty} k\dfrac{1\times Q}{x^2}dx\\\\
&=&\left[k\dfrac{1\times Qx^{(-2+1)}}{-2+1} \right]_r^{\infty}\\\\
&=&k\dfrac{Q}{r}
\end{eqnarray}

これが電荷 $q$ に対する電位 $V$ となります。
つまり、

$V=k\dfrac{Q}{r}$

ですね。

そうすると、電荷 $q$ が $Q$ の電荷から $r$ だけ離れているときに持つ位置のエネルギー $U$ は、
$1\:[\mathrm{c}]$ のときのエネルギーが $V$ なので $q$ では、 $U=qV=q\times k\dfrac{Q}{r}=k\dfrac{qQ}{r}$
となります。

この位置エネルギーと電位のイメージができると空間の把握が簡単にできるようになります。
ここまではぜひ理解しておきましょう。

電位差とはなにか

次に電位差（電圧）について考えてみましょう。
電位差は2点間の電位の差です。
そのままですが・・・・。

例えば、A地点とB地点の電位差は、
無限遠から考えたA地点の電位と、同じく無限遠から考えたB地点の地点の電位の差です。
厳密に言えば、この場合の電位の基準点はどこでも良いのですが、簡単のためとりあえずここでは無限遠を基準として考えてみましょう。

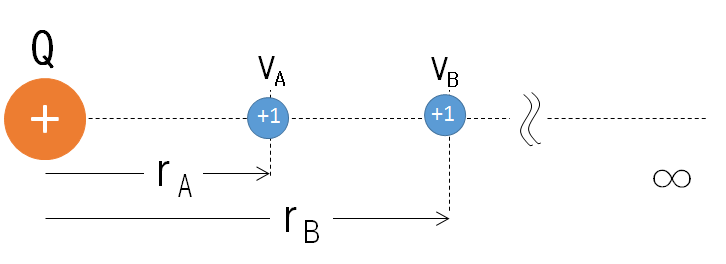
図のように無限遠から考えたA地点の電位 $V_A$ と、同じく無限遠から考えたB地点の地点の電位 $V_B$ を引けば出てきます。これが電位差（電圧）とされているものです。

電位の式は $V=k\dfrac{Q}{r}$ ですから、$r$ を $x$ として $V=k\dfrac{Q}{x}$ をグラフにしてみましょう。
そうすると、次のようなグラフになるはずです。

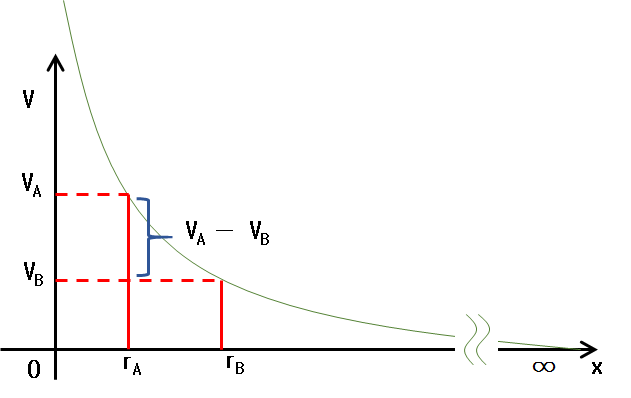
そして、2点間の電位差が $V$ であるとき、その間で $1\:[\mathrm{c}]$ の電荷を持つ物体を動かすには $V\:[\mathrm{J}]$ の仕事やエネルギーが出入りするというわけです。

ここまでくれば、電位差を求める場合、電位の基準はどこでも同じというのはご理解いただけると思います。
電位差とは、要するに差なので、どのように基準をとっても差は同じ、というわけです。
例えば、 $x$ 軸上の2点の差は原点をどこにとってもいつも同じですね。

１V の定義とは

電位、電位差、電圧の単位は V [ボルト] です。

電位の定義に従って考えてみます。
$1\:[\mathrm{c}]$ あたりの位置エネルギーでしたね。
つまり、

$V=\dfrac{U}{q}$

です。ということは、

$1\:[\mathrm{V}]=\dfrac{1\:[\mathrm{J}]}{1\:[\mathrm{c}]}$

となりますから、$1\:[\mathrm{V}]$ は $1\:[\mathrm{c}]$ の電荷を運ぶときに $1\:[\mathrm{J}]$ の仕事を要するということになります。

そうすると、 $1\:[\mathrm{V}]$ の間では、$2\:[\mathrm{c}]$ の電荷を運ぶときにはその倍の $2\:[\mathrm{J}]$ の仕事を要するということです。

また、$V\:[\mathrm{V}]$ は $1\:[\mathrm{c}]$ の電荷を運ぶときに $V\:[\mathrm{J}]$ の仕事を要するということになります。

つまり、電気量 $q$ の電荷を $V$ の電位差の間で移動するときの仕事・エネルギーの出入りは

$W=qV$

ということになります。
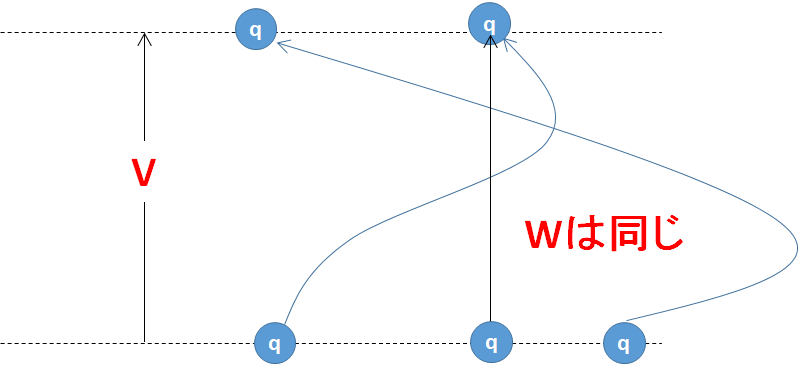
この仕事 $W$ は、2点間の電位差 $V$ がわかれば一つに決まります。
2点間をどのように動いても同じです。
つまりクーロン力は保存力です。

まとめ

では今回のおさらいをしてみましょう。

電位は、電気の世界の仕事・エネルギーを表しています。

電位は、$1\:[\mathrm{c}]$ あたりの電気的な位置エネルギー。
よって、電荷 $q$ のもつ位置エネルギーが $U$ であるとき、電位 $V$ は

$V=\dfrac{U}{q}$

となります。

点電荷 $Q$ から $r$ だけ離れた電位 $V$ は次の式で示されます。

$V=k\dfrac{Q}{r}$

よって、その地点の電荷 $q$ が持つ位置エネルギー $U$ は、

$U=qV=k\dfrac{qQ}{r}$

となります。

また、$1\:[\mathrm{V}]$ は $1\:[\mathrm{c}]$ の電荷を運ぶときに $1\:[\mathrm{J}]$ の仕事を要するということです。

電気量 $q$ の電荷を $V$ の電位差の間で移動するときの仕事・エネルギーの出入りは

$W=qV$

ということになります。

今回は基本的なイメージを構築できる！ということを目標にやってきました。
次回はさらに一様な電場と電位、等電位面、エネルギーの原理、などについて解説予定です。

動画でも解説したいと思っていますが、なかなか進みません。
しかし今は昔と違ってスタディサプリのようなサービスがあるのでこちらもオススメです。
【スタディサプリ】動画授業で苦手を克服
私の動画もよろしくお願いいたします。できましたらチャンネル登録をお願いします。
koko物理 物理解説チャンネル