気体分子運動論
高校物理の教科書で、気体分子運動論には、かなりのページが割かれています。
ここをきちんと授業で消化しようとすれば、とても1時間では終わらないでしょう。
それゆえ、すっ飛ばしの対象になることも多いと思われます。
ここでは、気体分子の運動から内部エネルギーを導出するところまでを、丁寧に解説したいと思います。
議論が長いので、途中で迷子になりやすいですね。
論理の進め方は以下のようになっています。
３．気体分子1個が1回の衝突で、一つの壁が受ける力積を計算する
６．算出した圧力の式と気体状態方程式から、気体分子1個の平均運動エネルギーを求める
７．$N$ 個の気体分子の運動エネルギー総和に拡張することで、気体内部エネルギーを求める
準備として、一辺の長さ $L$ の立方体の断熱容器（箱）を用意し、中に総数 $N$ 個の理想気体単原子分子を封入します。
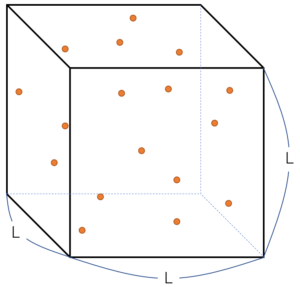
前提となる知識などのお話
まずは、基礎のおさらいから行きましょう。
もうわかっている・・・という方は飛ばしてください。
ミクロ的に見た気体の圧力
「気体の圧力とはなにか」と問われて何と答えるでしょうか？
気体はミクロな分子からなり、それが温度に応じた速さで、空中を飛び回っています。
「ある壁が受ける気体による圧力を考えるとき、それは個々の気体分子が壁にぶつかるためである」・・・と考えます。
そして、古典的な力学的手法を用いて壁が受ける気体からの圧力、ひいては気体の内部エネルギーまでを求めてみよう、というのです。
分子の小ささと数
気体分子の数は膨大で、アボガドロの法則から、 22.4 リットルで、だいたい $1 \:\mathrm{mol} $ と考えて、その中には $6.02\times 10^{23}$ 個の数の分子があります。
私たちの肺の容積が 3 リットルくらいだとすると、肺の中にある気体分子の数は、およそ $0.80\times 10^{23}$ 個ということになります。
これは、800,0000,0000,0000,0000,0000 個です。（4桁区切りにしてみました）
800 垓(がい)個・・・もはや絶対に、日常で扱うことのない単位です。（1垓は1兆の1億倍）
大きすぎてわかりませんね。
その大きさを示すたとえがあります。
- コップの水を一度全世界にぶちまけてよく攪拌したとします。
そうしておいて、海や川へ行って再びコップ一杯水を汲んだ時に、あなたのコップの中には元のコップにいた水分子が数百個含まれることになります。 - あるいはこんな話もあります、シーザーが死んだときの彼の肺の中にあった空気の分子のうち、その何個かは、いま、私たちの肺にある！
ほんとかいな？と疑うような話ですが、これは嘘ではなく、計算するとそうなるのです。
まあ、私たちの周りには、とにかくとてつもない数の気体分子がぶんぶん飛び回っているらしい、ということですね。
分子一つ一つはとても軽いため、ぶつかってもあまり影響はないように思いますが、上に示したような膨大な数ともなると話が変わってきます。
He ヘリウムの原子量はほぼ 4 ですから、22.4 リットルで約 4 g しかありません。
そのうえ、その 4 g の中には膨大な数のヘリウム原子（単原子分子）がありますから、分子一つの質量は、文字通り吹けば飛ぶほどしかないのです。
しかし、それでも、数のパワーで押しまくるため、壁はかなり大きい力を受けることになります。
ここでちょっと、大気圧の大きさを計算してみましょう。
大気圧の大きさ
地表での大気による圧力をだいたい、$1.0\times 10^5\:\mathrm{[Pa]}$ としましょう。
この数値の意味は、$1.0\times 10^5\:\mathrm{[N/m^2]}$ です。
だいたい、質量 $100\:[g]$ の物体にかかる重力の大きさが $1\:[\mathrm{N}]$ でしたから、$1\:[\mathrm{m^2}]$ に $10000\:[\mathrm{kg}]=10\:[\mathrm{t}]$ の質量のものが乗っているときの圧力と同じです。
そうすると、$1\:[\mathrm{m^2}]=10^4\:[\mathrm{cm^2}]$ ですから、
$10000 \:[\mathrm{kgf}] \div 10^4\:[\mathrm{cm^2}]=1\:[\mathrm{kgf/cm^2}]$
つまり、$1\:[\mathrm{cm^2}]$ に$1\:[\mathrm{kgf}]$ のものを乗せているのと同じということになります。
小指の爪の上に $1\:[\mathrm{kg}]$ の質量のおもりが乗っていると想像してください。
よくつぶれませんねぇ。
計算の準備編
分子運動と圧力
では、気体による圧力を具体的に考えていきます。
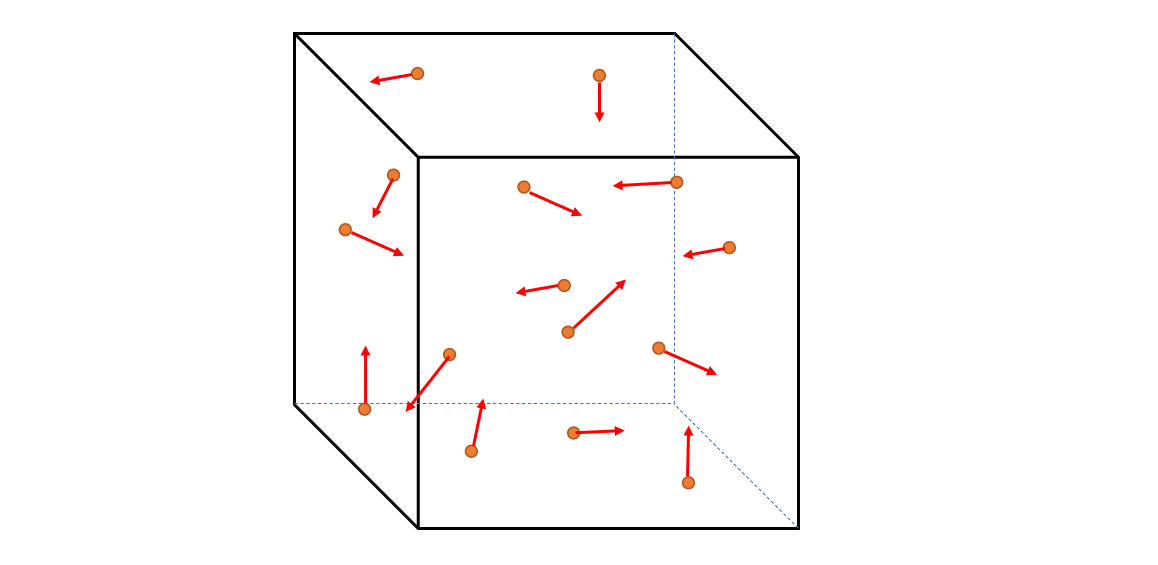
図のような断熱性の容器（箱）を考えます。（どのような容器でもいいのですが、計算が容易なものを考えます）
容器の一辺の長さを $L$ の立方体とします。よって、壁の面積は $L^2$ で、立方体の体積は $L^3$ です。
さて、この中に $N$ 個の理想気体単原子分子を閉じ込めます。
その気体分子の1個の質量を $m$ としましょう。
この分子の飛ぶ方向はランダムです。
そして壁とぶつかり、壁に力を及ぼします。
気体分子は壁と弾性衝突する
気体分子と壁は弾性衝突します。
なぜそんなことが言えるのでしょうか？
日常世界を見ていると、弾性衝突するものなど
ほぼ無いように思います。
気体温度が一定であるという条件下ではそうなります。
一つ一つの分子を見ていれば、中には壁に衝突して遅くなるのもあるでしょうし、速くなるのもあるでしょう。
しかし、全体として見れば、分子が壁にぶつかる前と後では速さは同じとして構わないのです。
なぜなら、この場合、断熱性の箱に入れているわけで、そうすると、外部とのエネルギーの交換はありません。
したがって、箱の中の全分子の運動エネルギー総和は変化しません。
よって、全体としてみるとき、分子の運動エネルギーは不変です。
したがって、壁といろいろなやり取りはあるかもしれませんが、平均的には壁に衝突する前後での速さ変化はない、と考えて差し支えないのです。
あるいは、外部と熱平衡状態であると考えた場合も同じく、壁に衝突する前後での平均の速さの変化はありません。
どちらにしろ、衝突の前後での速さに変化がないため、$e=-\dfrac{v’}{v}$ より、$e=1$ であり、弾性衝突するといえるわけです。
気体分子1個が1回の衝突で、一つの壁が受ける力積を計算する
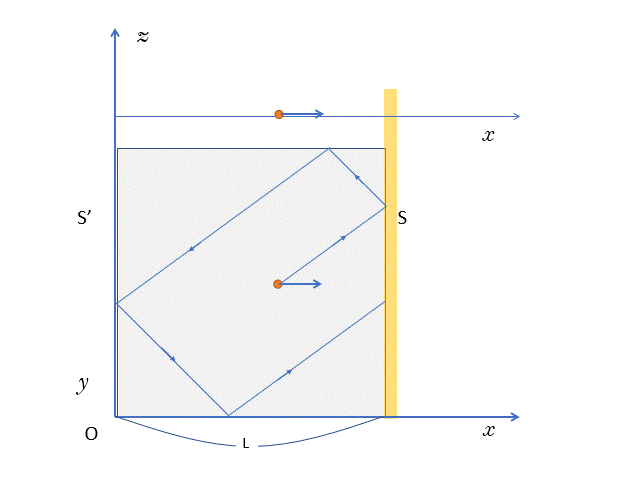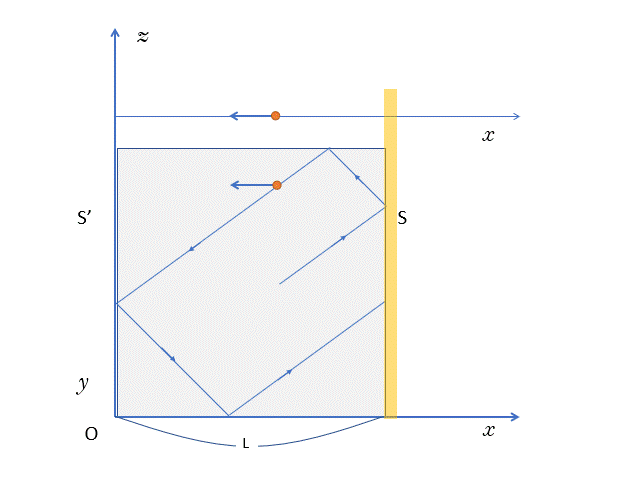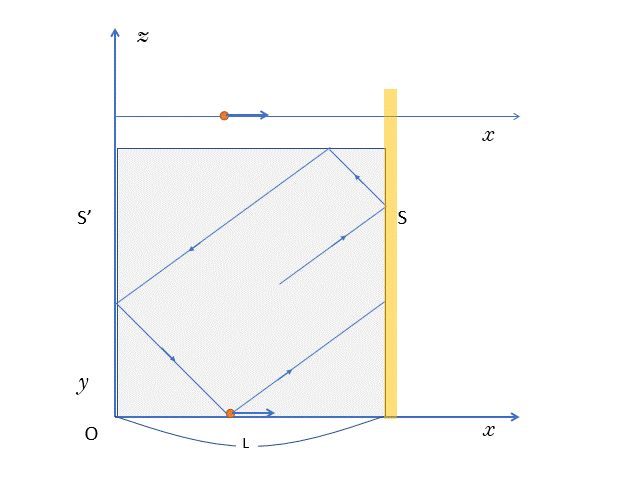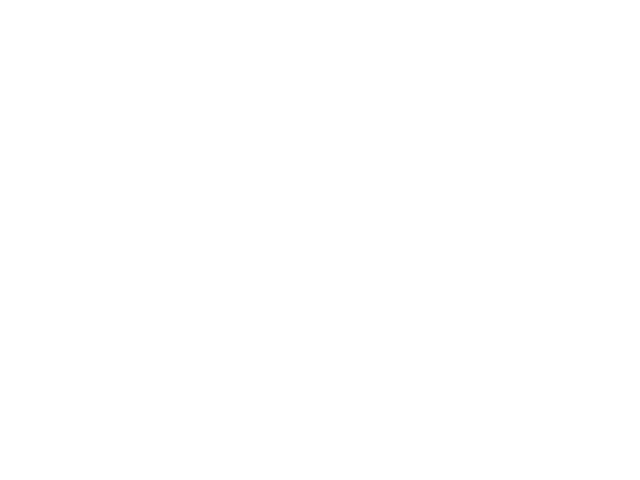
図のように $x,\:y,\:z$ 軸をとったとき、ある一つの分子の飛ぶ速度を ${v}=(v_x,v_y,v_z)$ とできます。
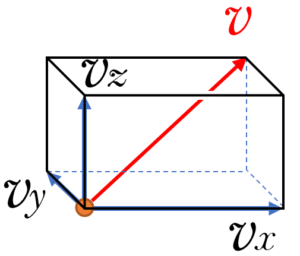
そして、壁とは弾性衝突するわけですから、それぞれの速度成分は衝突に際して方向が変わるだけで、その大きさは変わりません。
さて、今回は図の $x$ 方向にある壁 $S$ について考えることにします。
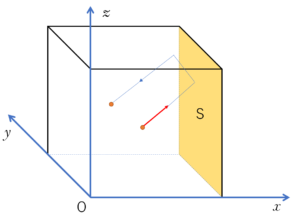
そうすると、壁 $S$ に速度 $v_x$ で当たった後は、$-v_x$ で跳ね返ってきます。
そうして、反対側の壁 $S’$ で $v_x$ で跳ね返ります。
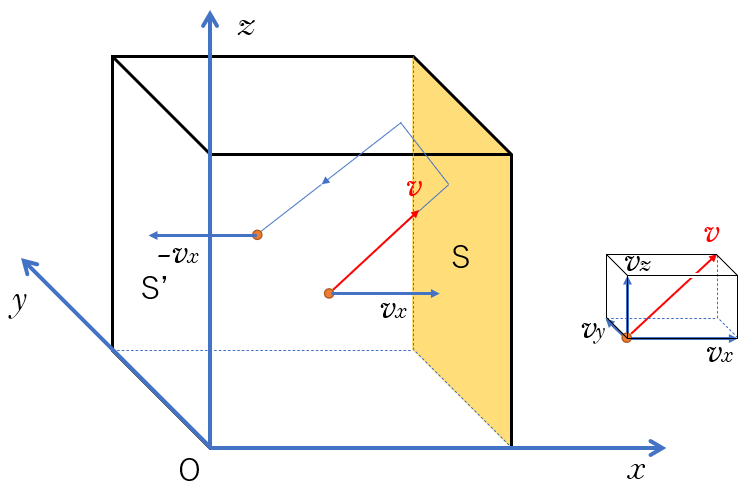
つまり、$x$ 軸方向だけで見ると、壁 $S$と$S’$ の間を同じ速さで往復運動していることになります。
ここの理解が最初は難しいようです。
図をよく見てしっかり理解してください。
したがって、壁 $S$ がうける力を考える際には、次の図のように $x$ 軸方向に平行に運動する粒子を考えればよいことになります。
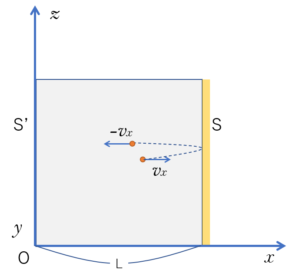
実際は、壁にぶつかる位置は毎回違いますが、壁の受ける力や圧力を計算する場合には、問題ありません。
では、壁 $S$ への1回の衝突の前後での、1個の気体分子の運動量変化を考えてみます。
気体分子1個の速度は、${v}=(v_x,v_y,v_z)$ と表したのでした。
$x$ 軸方向のみを考えるので、1回の壁への衝突では、
$衝突前の運動量=mv_x$
$ 衝突後の運動量=-mv_x$
です。
さて、正負に注意して、力積 $I$ と運動量の関係から、
$$mv_x+I=-mv_x$$
$$I=-2mv_x$$
(最初の運動量)＋(力積)＝(後の運動量)
と考えましょう。
このときの力積 $I$ は、1回の衝突で 壁が気体分子に及ぼす 力積です。
つまり気体分子が受けているということです。
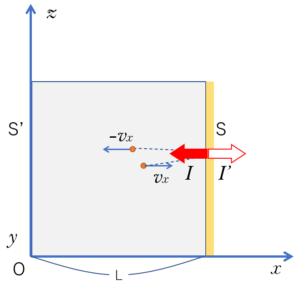
今は、壁が受ける力積や力を知りたいので、この作用・反作用の関係にある 気体分子が壁に及ぼす 力積を知る必要があります。
そしてそれは、方向が逆なため、$I’=-I$ と示されます。
したがって、気体分子1個が1回壁に衝突した場合の壁が受ける力積は、$I’=-I=2mv_x$ となります。
まとめ
気体分子1個が1回壁に衝突した場合、壁が受ける力積
$I’=2mv_x$
1個の分子が、壁に与える平均の力を求める
気体分子が壁を往復する時間
ここでは、気体分子が壁 $S$ に衝突してから、次にもう一度壁 $S$ に衝突するまでの時間 $T$ を求めます。
まあ、衝突周期 $T$ といってもいいでしょう。
これにより、単位時間（1秒）当たりの気体分子の壁 $S$ への衝突回数がわかります。
そうすることで、時間 $t$ での、気体分子と壁 $S$ との衝突回数を求めます。
では求めていきましょう。
気体分子が $x$ 軸方向に運動するとします。
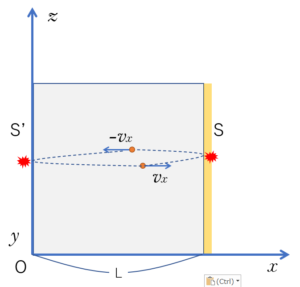
図より、長さ $2L$ の距離を $x$ 軸方向の速さ $v_x$ で運動しますから、壁 $S-S’-S$ と、往復に要する時間 $T$ は、
$$T=\dfrac{2L}{v_x}$$
です。
ちなみに、箱を真横から見ると、実際は次の図のように運動しているはずです。
このとき、$x$ 軸方向の速さは $v_x$ で一定のため、
$x$ 軸方向だけに運動している場合と比べても、往復時間や、壁 $S$ への衝突回数に違いがないことがわかると思います。
気体分子が時間 $t$ のあいだに壁 $S$ に衝突する回数
先ほどの計算により、壁 $S-S’-S$ と、往復する時間 $T$ は、
$$T=\dfrac{2L}{v_x}$$
です。
このとき、1往復で1回、壁 $S$ に衝突します。
つまり、 時間 $T$ で、1回往復し、壁 $S$ に1回衝突するわけです。
では、 時間 $t$ では壁 $S$ に $n$ 衝突するとして、
$$T:1=t:n$$
より、$n=\dfrac{t}{T}$ ですね。
したがって、
\begin{eqnarray}
n&=&\dfrac{t}{T}\\\\
&=&\dfrac{t}{\dfrac{2L}{v_x}}\\\\
n&=&\dfrac{v_xt}{2L}
\end{eqnarray}
となります。
壁が1つの気体分子から受ける平均の力
前に計算した、「壁気体分子1個が1回の衝突で、一つの壁が受ける力積を計算する」より、壁 $S$ は気体分子1個から1回の衝突で、力積 $I’=2mv_x$ を受けることがわかっています。
そして、時間 $t$ では、$n=\dfrac{v_xt}{2L}$ 回 だけ衝突しますから、その時に壁 $S$ が気体分子1個から受ける力積の総和は
\begin{eqnarray}
n\times (I’)&=&n \times (2mv_x)\\\\
&=&\left( \dfrac{v_xt}{2L}\right)\times 2mv_x\\\\
&=&\dfrac{mv^2_x}{L}t
\end{eqnarray}
となります。
この、時間 $t$ で受けた力の平均 $\overline{f}$ を考えるとします。だから
そうすると、$力積=力\times 時間$ つまり、$\overline{f}\times t $ で、力積の総和が、$ \dfrac{mv^2_x}{L}t$ でしたので、
\begin{eqnarray}
\overline{f}\times t &=& \dfrac{mv^2_x}{L}t\\\
\overline{f}&=& \dfrac{mv^2_x}{L}
\end{eqnarray}
となります。
まとめ
気体分子1個が時間 $t$ の間に、壁 $S$ に及ぼす平均の力 $\overline{f}$
$\overline{f}= \dfrac{mv^2_x}{L}$
壁が受ける圧力を計算する
壁 $S$ が $N$ 個の分子から受ける平均の力
いままでは、気体分子1個だけの話です。
実際は、気体分子は非常に多くあり、それらが壁に力を及ぼすことで圧力を生じています。
今、気体分子総数が $N$ 個のとき、それらすべての気体分子が壁 $S$ に及ぼす平均の力を $\overline{F}$ とすると、
\begin{eqnarray}
\overline{F}&=&N\times \overline{f}
\end{eqnarray}
です。ここで、$\overline{f}= \dfrac{mv^2_x}{L}$ でした。
しかし、この時の $v_x$ は1個の分子の速さを示しています。
これから、全体の平均を考えようとしています
したがって、総数 $N$ 個の気体分子の平均の速さの2乗の平均 $\overline{v^2_x}$ を考えることにします。
そうすると、$\overline{f}=\dfrac{m\overline{v^2_x}}{L}$
\begin{eqnarray}
\overline{F}&=&N\times \overline{f}\\\\
\overline{F}&=& \dfrac{Nm\overline{v^2_x}}{L}\\\\
\end{eqnarray}
となります。
壁 $S$ が $N$ 個の分子から受ける平均の圧力
いよいよ、壁 $S$ が受ける圧力 $p$ を計算します。
ここで、壁 $S$ の面積は $L\times L=L^2$ です、そして、$\overline{F}=N\dfrac{Nm\overline{v^2_x}}{L}$ より、
$圧力=\dfrac{力}{面積}$ です
\begin{eqnarray}
p&=&\dfrac{\overline{F}}{L^2}\\\\
&=&\dfrac{\left(\dfrac{Nm\overline{v^2_x}}{L}\right)}{L^2}\\\\
&=&\dfrac{Nm\overline{v^2_x}}{L^3}\\\\
\end{eqnarray}
さて、ここで容器の体積 $V$ は、$V=L^3$ であることから、
$$p=\dfrac{Nm\overline{v^2_x}}{V}$$
とできます。
もう一息ですが、今の式を見ると $x$ 軸方向の速さ $v_x$ を使用しているため、実際には計算は難しいでしょう。
それを解消するため、$v_x$ をもとの気体分子の速さ $v$ で示すことを考えます。
空間のベクトル図から、三平方の定理を用いて、$v^2=v_x^2+v_y^2+v_z^2$ となります。
ここで、$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}$ が成り立つとします。
分子数は極めて多数です。参考はここ
そのため、$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$ であると考えられそうです。
となると、$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}=3\overline{v_x^2}$ より、
$$\overline{v_x^2}=\dfrac{1}{3}\overline{v^2}$$
となります。
したがって、
\begin{eqnarray}
p&=&\dfrac{Nm\overline{v^2_x}}{V}\\\\
&=&\dfrac{Nm\left(\dfrac{1}{3}\overline{v^2} \right)}{V}\\\\
p&=&\dfrac{Nm \overline{v^2}}{3V}\\\\
\end{eqnarray}
となり、圧力の式を導くことができました。
まとめ
壁が受ける平均の力
$\overline{F}=\dfrac{Nm\overline{v^2_x}}{L}$
壁が受ける圧力
$p=\dfrac{Nm \overline{v^2}}{3V}$
算出した圧力の式と気体状態方程式から、気体分子1個の平均運動エネルギーを求める
前項の式、$p=\dfrac{Nm \overline{v^2}}{3V}$ へ状態方程式 $pV=nRT$ （$n$ はモル数）より、$p=\dfrac{nRT}{V}$ として代入します。
\begin{eqnarray}
p&=&\dfrac{Nm \overline{v^2}}{3V}\\\\
\left(\dfrac{nRT}{V}\right)&=&\dfrac{Nm \overline{v^2}}{3V}\\\\
nRT&=&\dfrac{Nm\overline{v^2}}{3}\\\\
\end{eqnarray}
これから式を変形して、運動エネルギー $\dfrac{1}{2}m\overline{v^2}$ を取り出します。
\begin{eqnarray}
\dfrac{Nm\overline{v^2}}{3}&=&nRT\\\\
\dfrac{1}{2}m\overline{v^2}&=&\dfrac{3nRT}{2N}\\\\
&=&\dfrac{3nRT}{2(nN_A)} \:\:\:\:\:\:\:\:\:(N=nN_A \:\:\:\:\: N_A：アボガドロ数)\\\\
&=&\dfrac{3}{2} \left( \dfrac{R}{N_A}\right) T\\\\
\end{eqnarray}
ここで、 $\dfrac{R}{N_A}=k$（定数）と置くと、
\begin{eqnarray}
\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT\\\\
\end{eqnarray}
となります。この $k$ をボルツマン定数と呼びます。
このとき、$x,\:y,\:z$ 軸を考えれば、それぞれの軸方向に $\dfrac{1}{2}kT$ ずつ、エネルギーが等しく分配されていると考えることもできます。
これを等分配の法則と呼びます。もっと言えば、1自由度に対して、 $\dfrac{1}{2}kT$ ずつ等分配されています。
自由度に関しては
新しく記事をアップします
分子が単原子ではなく、2原子であれば、回転や振動のエネルギーが加わるため、分子の運動エネルギーは $\dfrac{5}{2}kT$ となります。
2乗平均速度
$\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT$ より
\begin{eqnarray}
\dfrac{1}{2}m\overline{v^2}&=&\dfrac{3}{2}kT\\\\
&=&\dfrac{3}{2}\dfrac{R}{N_A}T\\\\
\overline{v^2}&=&\dfrac{3RT}{mN_A}\\\\\\\\
\sqrt{\overline{v^2}}&=&\sqrt{\dfrac{3RT}{mN_A}}\\\\
\end{eqnarray}
ここで気体のモル質量 $M$とすると、$M=mN_A$ であるから
\begin{eqnarray}
\sqrt{\overline{v^2}}&=&\sqrt{\dfrac{3RT}{mN_A}}\\\\
&=&\sqrt{\dfrac{3RT}{M}}\\\\
\end{eqnarray}
となる。これを2乗平均速度と呼びます。
注意
ここで $1\:\mathrm{mol}$ あたりの質量を $M$ としました。
$1\:\mathrm{mol}$ での分子の個数 $N_A$ であるから、分子1個の質量を $m$ とした場合、$m\times N_A=M$ となります。
化学では $M$ の単位として $\mathrm{g/mol}$ を用いることが多いですね。
物理では、一般には質量単位として $\mathrm{kg}$ を用います。
この場合、単位に注意して計算すべきです。
もし、 $M$ の単位として $\mathrm{g/mol}$ を用いたとすると、先ほどの式は、
$\sqrt{\overline{v^2}}=\sqrt{\dfrac{3RT}{M\times 10^{-3}}}$
となることに注意してください。
＄まとめ
単原子分子1個の平均運動エネルギー $k$：ボルツマン定数 $k=\dfrac{R}{N_A}$
$\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT$
2原子分子の場合 $\dfrac{5}{2}kT$
2乗平均速度 Mの単位に注意
$\sqrt{\overline{v^2}}=\sqrt{\dfrac{3RT}{M}}$
$N$ 個の気体分子の運動エネルギー総和に拡張することで、気体内部エネルギーを求める
ここまで長い道のりでした。もうあと少しです。
では、気体の内部エネルギー $U$ の式を求めましょう。
前項のまとめから、気体分子1個の平均運動エネルギーは $\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT$ でした。
気体分子総数は $N$ 個ですから、気体の分子全部の運動エネルギー総和は、$N$ 倍するだけです。
そして、分子間の相互の力を考慮しない理想気体の場合、気体の分子全部の運動エネルギー総和を気体内部エネルギー $U$ としてもよさそうです。
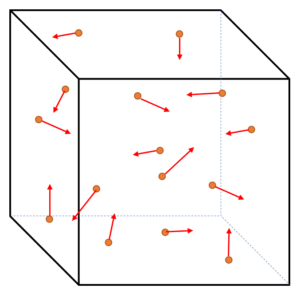
したがって、
\begin{eqnarray}
U&=&N\times \left( \dfrac{1}{2}m\overline{v^2}\right)\\\\
&=&N\times \dfrac{3}{2}kT\:\:\:\:\:\:\:\:\:\:(k=\dfrac{R}{N_A} )\\\\
&=&N\times \dfrac{3}{2}\left(\dfrac{R}{N_A}\right)T \:\:\:\:\:\:\:\:\:\:(N=nN_A)\\\\\
&=&\left(nN_A\right)\times \dfrac{3}{2}\left(\dfrac{R}{N_A}\right)T \\\\\\
U&=&\dfrac{3}{2}nRT \\\\\\
\end{eqnarray}
この式からわかる大事なことは、単原子分子理想気体の内部エネルギー $U$ は、気体モル数 $n$ と気体の絶対温度 $T$ で決まるということです。
もし、気体のモル数 $n$ が同じなら、気体の絶対温度だけで決まります。
また、気体が状態変化したときの内部エネルギーの増減分 $\Delta U$ は、温絶対度が $\Delta T$ だけ変化した場合
\begin{eqnarray}
\Delta U&=&\dfrac{3}{2}nR(T+\Delta T)-\dfrac{3}{2}nRT \\\\\\
&=&\dfrac{3}{2}nR\Delta T
\end{eqnarray}
となります。
この式は非常によく使う重要な式です。
まとめ
単原子分子理想気体の内部エネルギー $U$
$U=\dfrac{3}{2}nRT$
単原子分子理想気体の内部エネルギー変化分 $\Delta U$
$\Delta U=\dfrac{3}{2}nR\Delta T$
最後に
結論をまとめておきましょう。
単原子分子1個の平均運動エネルギー $k$：ボルツマン定数 $k=\dfrac{R}{N_A}$
$\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT$
2原子分子の場合 $\dfrac{5}{2}kT$
2乗平均速度 Mの単位に注意
$\sqrt{\overline{v^2}}=\sqrt{\dfrac{3RT}{M}}$
単原子分子理想気体の内部エネルギー $U$
$U=\dfrac{3}{2}nRT$
単原子分子理想気体の内部エネルギー変化分 $\Delta U$
$\Delta U=\dfrac{3}{2}nR\Delta T$
コメント