反発係数 物理のエッセンス 力学 12番
物理のエッセンスの力学12番**の問題について解説します。
物理のエッセンスP14を開いてください。
問題の概要
物理のエッセンスP14を開いてください。
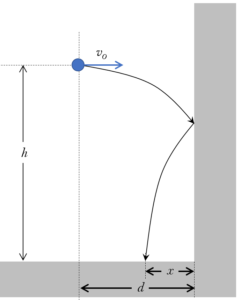
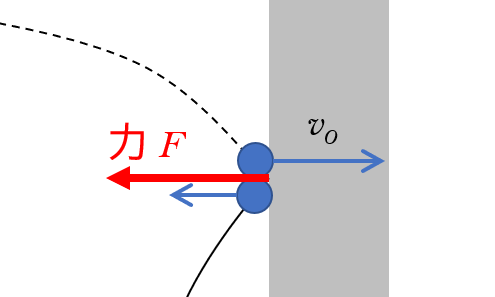
垂直な壁に向かって物体を水平投射して初速 $v_0$ でぶつけます。壁との反発係数が $e$ として、床に達するまでの時間と落下点と壁との距離 $x$ を求めます。
解説
落下時間
まず、壁と物体の間に摩擦はないので、衝突の際に物体が壁から受ける力は、図の壁に垂直方向の力 $F$ だけです。
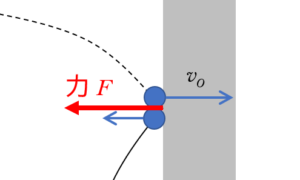
したがって、ニュートンの運動の第2法則( $ma=F$ )により、この力は水平方向の速度だけを変化させて、鉛直方向の速度には影響を及ぼしません。

ニュートンの運動の第2法則
物体に力を加えると加速度を生じ、その向きは力の向きと同じである。
加速度の大きさは力の大きさに比例し、質量に反比例する。
加速度の向きと力の向きは必ず一致します!!
ということは・・・・。
そうですね、最初に水平投射しているので、たとえ壁にぶつかろうが鉛直方向の速度は変化しない。つまり、「鉛直方向には自由落下している」と考えて構わないのです。
最初の問題の方針ができました。
床につくまでの時間 $t$ は、高さ $h$ からの自由落下にかかる時間と同じである。
つまり、 $y=\dfrac{1}{2}gt^2$ に従います。
よって、重力加速度が $g$ なので、
$t=\sqrt{\dfrac{2h}{g}}$
となります。
壁との距離
ついで、落下地点の床との距離 $x$ を求めましょう。
物体が壁にぶつかるまでの時間を $t_1$ とします。
そうすると、水平方向には、速さ $v_0$ で等速運動しますから、単純に、 時間=距離 ÷ 速さ より
$t_1=\dfrac{d}{v_0}$
と示されます。
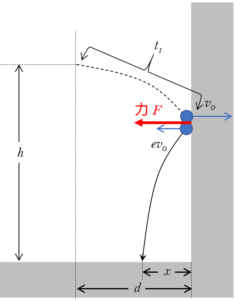
そうすると、物体が壁にぶつかってから床に落ちるまでの時間は、 $t-t_1$ になります。
ここで、$t$ は最初に求めた、水平投射してから床に到達するまでの時間です。$t=\sqrt{\dfrac{2h}{g}}$
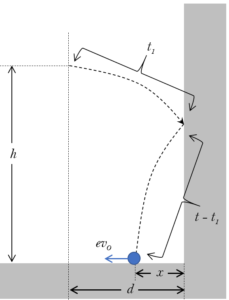
物体は壁にぶつかって、跳ね返りますが、跳ね返った後の水平方向の速さは反発係数 $e$ より、$ev_0$ で逆向きになります。

反発係数 $e$ は
$e=-\dfrac{v’}{v}$
で示されます。
さて、肝心の $x$ ですが、これは壁にぶつかってから $t-t_1$ の時間がかかって、床に落下します。
そして、水平方向には $ev_0$ の速さで進むわけですから、$x$ は、 速さ × 時間 より
$x=(ev_0)\times (t-t_1)$
$~~~=(ev_0)\times \left(\sqrt{\dfrac{2h}{g}}-\dfrac{d}{v_0}\right)$
$~~~=e\left(v_0\sqrt{\dfrac{2h}{g}}-d\right)$
となります。




































コメント