運動量と相対速度 物理のエッセンス力学74番
この問題に限らず、相対速度を考えるときにはその正負が難しいと感じる方が多くみえるようです。
ここでは、物理のエッセンスの力学編74番を題材に、運動量と相対速度について考えていきましょう。
動画
問題の概要 ロケットの噴射
問題の詳細については、物理のエッセンスの力学編P60をご覧ください。
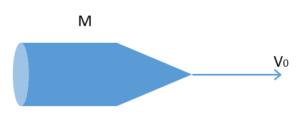
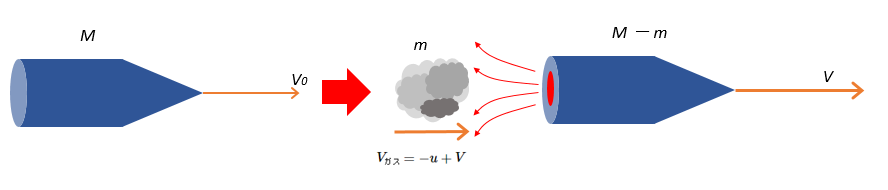
宇宙空間を速さ $V_0$ で進む質量 $M$ のロケットから、ロケットから見て速さ $u$ で質量 $m$ のガスを後方へ噴射した。ロケットの速さ $V$ はいくらになるか・・・。という問題です。
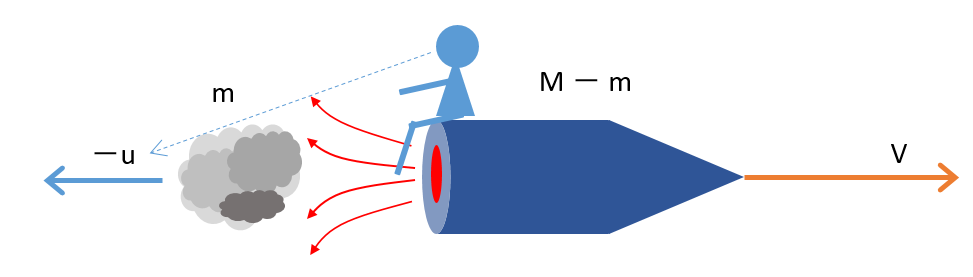
この問題で難しいのは、噴出したガスがロケットから見て後方に速さ $u$ で遠ざかった、という点です。相対速度を考えて対応します。
では、ここで相対速度のおさらいをしましょう。
相対速度
B から見た A の相対速度 $V_{BA} $ は、次の式で示されます。
$V_{BA}=V_A-V_B$
相対速度については、以下の記事を参考にしてください。

ではここで、「噴出したガスがロケットから見て後方に速さ $u$ で遠ざかった」について相対速度の式を立てて見ます。
まず、ロケットを見ることができる、静止している点を想像します。
このとき、ロケットから観測したガスの速度は相対速度であることに注意します。
一方、問題文に示されているロケットの速度は、静止地点から観測した速度を意味しています。
ここではわかりやすいように、
- ロケットから見たガスの相対速度を $V_{(ロケ)(ガス)}$
- 静止している点から見たロケットの速度を $V_{ロケ}$
- 静止している点から見たガスの速度を $V_{ガス}$
とします。そうすると、次の図のようなイメージになります。
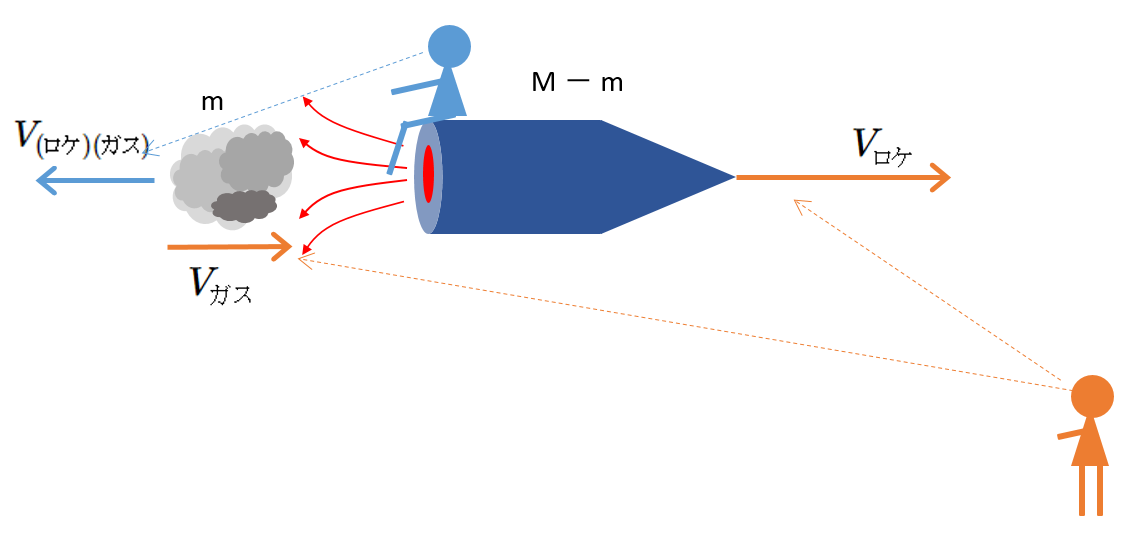
このとき、 $V_{BA}=V_A-V_B$ から、次式が成り立つはずです。
すなわち、
$V_{(ロケ)(ガス)}=V_{ガス}-V_{ロケ}$
です。
ここで、図の右方向を正方向としてやると、ロケットから見たガスの速度は $-u$ と示されます。
- $V_{(ロケ)(ガス)}=-u$ マイナスがつくことに注意してください。
- $V_{ロケ}=V$
なので、次のように書き換えましょう。
$V_{(ロケ)(ガス)}=V_{ガス}-V_{ロケ}$ より、
$-u=V_{ガス}-V$
よって、これを変形して、
$V_{ガス}=-u+V$
となります。つまり、静止地点から観測すると、ガスの速度は $V_{ガス}=-u+V$ で示されます。
さて、ここで運動量保存則を考えます。
運動量保存則
ガス噴射前の総運動量=ガス噴射後の総運動量
ですから、
\begin{eqnarray}
MV_0&=&mV_{ガス}+(M-m)V ここで、V_{ガス}=-u+V より、\\\\
&=&m(-u+V)+(M-m)V
\end{eqnarray}
より、
$V=\dfrac{MV_0+mu}{M}$
となります。




































コメント