今回は力率について解説します。高校物理ではあまり扱いませんが、理解しておきたいところです。
交流回路ではコイル・コンデンサーでは電力を消費しません。
したがって、回路全体の消費電力は抵抗におけるもので、
RLC直列回路では
$\overline{P}=I_eV_e \cos \phi=R{I_e}^2$
$ Z = \sqrt{ R^2+\left( \omega L \:- \dfrac{1}{\omega C } \right)^2 }$
$\cos \phi =\dfrac{R}{Z}=\dfrac{R}{\sqrt{R^2+\left( \omega L -\dfrac{1}{\omega C}\right )^2}}$
$\cos \phi = \dfrac{V_{R0}}{V_0}=\dfrac{V_{Re}}{V_e}$
RLC並列回路では
$\overline{P}=I_e V_e \cos \phi =\dfrac{{V_e}^2}{R} $
$ Z = \dfrac{1}{\sqrt{ \dfrac{1}{R^2} + \left( \omega C \:- \dfrac{1}{\omega L } \right)^2 }}$
$\cos \phi =\dfrac{Z}{R}=\dfrac{\dfrac{1}{R}}{\sqrt{\dfrac{1}{R^2}+\left( \omega C -\dfrac{1}{\omega L}\right )^2}}$
$\cos \phi=\dfrac{I_{R0}}{I_0}=\dfrac{I_{Re}}{I_e}$
$\cos\phi$ を力率と呼びます。 $ ( \:0 \leqq \cos \phi \leqq 1 \: )$
RLC直列回路と並列回路では力率の求め方が違うので注意。
$\overline{P}=I_e V_e \cos \phi $ を有効電力と呼び、単位には W(ワット)を用います。
それに対して、交流電圧の実効値と電流の実効値の積 $I_eV_e$ を皮相電力といいます。
皮相電力は単に名目上の電力であり、実際の消費電力ではありません。そのため、単位に W (ワット)は使わず、VA(ボルトアンペア)が使われます。
交流の式はエグいですが、覚えなければならないことはあまりありません。
電磁気の記事は次を参照してください。

力率と消費電力 交流の基礎7
コイル・コンデンサーにおける消費電力の時間平均は 0 です。
参考記事

したがって交流回路では基本的に、抵抗における消費電力についてのみ考えれば良いことになります。
以下、電源電圧の最大値を $V_0$ 実効値を $V_e$ で示します。
また、各素子の電圧・電流のそれぞれの最大値にも各素子を示す記号に添え字 $_0$ で、実効値は $_e$ で示します。
($R$ は抵抗、$L$ はコイル、$C$ はコンデンサーを示します)
例 コイルの電圧最大値 $V_{L0}$ 実効値 $V_{Le}$
電流最大値 $I_{L0}$ 実効値 $I_{Le}$
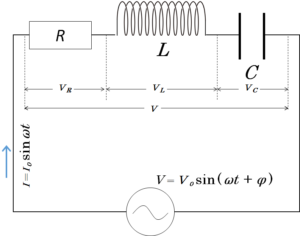
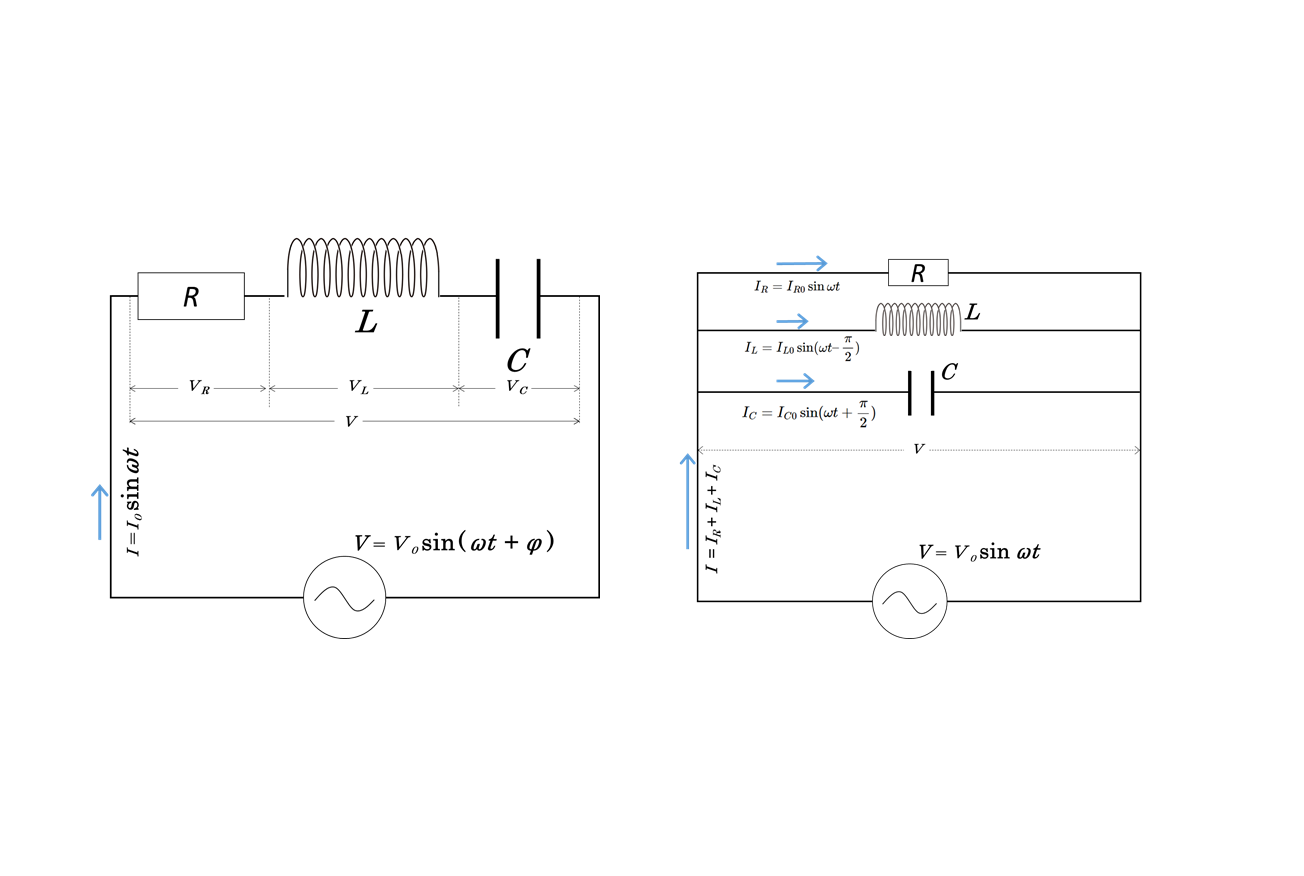
RLC直列回路

全体の電流 $I=I_0 \sin \omega t$
全体の電圧 $V=V_0\sin (\omega t + \phi)$
抵抗にかかる電圧 $V_R=V_{R0}\sin \omega t $
コイルにかかる電圧 $V_L=V_{L0}\sin (\omega t + \dfrac{\pi}{2})$
コンデンサーにかかる電圧 $V_C=V_{C0} \sin (\omega t \:- \dfrac{\pi}{2})$
$\tan \phi = \dfrac{\omega L \:- \cfrac{1}{\omega C}}{R}$
RLC直列 ・・・ 計算
全体の電流と電圧から計算すると
全体の電流 $I=I_0 \sin \omega t$
全体の電圧 $V=V_0\sin (\omega t + \phi)$
${P}=IV$
$~~~=I_0 \sin \omega t \times V_0\sin (\omega t + \phi)$
$~~~=I_0V_0 \sin \omega t \left( \sin \omega t \cos \phi + \cos \omega t \sin \phi \right ) \:\cdots\cdots$ 補
$~~~=I_0V_0 \left( \sin^2 \omega t \cos \phi + \sin \omega t \cos \omega t \sin \phi \right ) $
$~~~=I_0V_0 \left( \dfrac{1-\cos 2 \omega t}{2} \cos\phi + \dfrac{\sin 2 \omega t}{2} \sin \phi \right ) \:\cdots\cdots$ 補
時間平均を取るわけだから、 $\cos 2 \omega t = 0 $ $\sin 2 \omega t = 0 $ となる。
したがって、
$\overline{P}=I_0V_0 \dfrac{1}{2} \cos \phi $
$~~~=\dfrac{I_0}{\sqrt{2}}\dfrac{V_0}{\sqrt{2}} \cos\phi $
$~~~=I_e V_e \cos \phi $

$V_e=\dfrac{1}{\sqrt{2}}V_0$ $I_e=\dfrac{1}{\sqrt{2}}I_0$ を使いました。
つまり、この回路全体の消費電力は
$\mathrm{回路全体の消費電力}=\mathrm{(全体の電圧の実効値)} \times \mathrm{(全体の電流の実効値) }× \cos \phi $
という値になります。この $\cos \phi$ を力率と呼んでいます。
コイルとコンデンサーでは電力を消費しないため、回路全体での電力は抵抗のみで消費されます。

注: $\phi$ は定数のため、$\cos\phi$ も定数です。
したがって、$\cos\phi$ の時間平均 = 0 とはなりません。
RLC直列 ・・・ 図から
全体の消費電力を考えるには、コイルとコンデンサーの消費電力は 0 のため、抵抗のみについて考えればよい。
抵抗での消費電力は
$\overline{P} = I_{Re}V_{Re} $
$V_{Re}=RI_{Re}$ だから
$~~~=R{I_{Re}}^2$
抵抗を流れる電流は回路全体で共通だから $I_{Re}=I_e$
よって、
$\overline{P} =R{I_e}^2$
また、
抵抗の消費電力のみを考えるわけだから、抵抗にかかる電圧 $V_{Re}$ を考え、
図から、 $V_{R0}=V_0 \cos \phi \:\:\cdots\cdots (\ast) $ したがって、 $V_{Re}=V_e \cos \phi $ となります。
( $-\frac{\pi}{2} \leqq \phi \leqq \frac{\pi}{2} $ よって、 $ 0 \leqq \cos \phi \leqq 1$ )
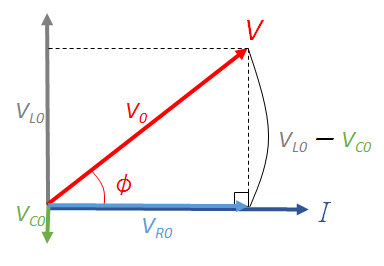
よって、

$\overline{P} = I_{Re}V_{Re} $
$~~~=I_{Re}V_e \cos \phi$
直列回路のため、抵抗を流れる電流は回路全体で共通だから $I_{Re}=I_e$
$\overline{P}=I_{e}V_e \cos \phi$
RLC直列 ・・・ 力率
力率 $\cos\phi$ については式 $(\ast)$ の $V_{R0}=V_0 \cos \phi$ より、
$\cos \phi=\dfrac{V_{R0}}{V_0}$
$V_0=ZI_0$ $V_{R0}=RI_{R0}=RI_0$ だから、
$\cos \phi=\dfrac{RI_0}{ZI_0} = \dfrac{R}{Z}$
RLC直列回路のインピーダンス $Z$ を代入する。 $Z=\sqrt{R^2+\left( \omega L -\dfrac{1}{\omega C} \right )^2 } $
$\cos \phi = \dfrac{R}{Z} = \dfrac{R}{\sqrt{R^2+\left( \omega L -\dfrac{1}{\omega C}\right )^2}}$
$-\dfrac{\pi}{2} \leqq \phi \leqq \dfrac{\pi}{2} $ $ 0 \leqq \cos \phi \leqq 1$
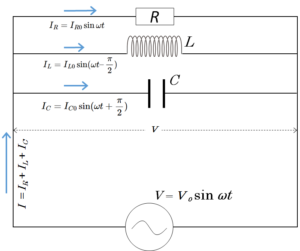
RLC並列回路
全体の電流 $I=I_0 \sin (\omega t + \phi)$
全体の電圧 $V=V_0\sin \omega t $
$\tan \phi = \dfrac{\omega C \:- \dfrac{1}{\omega L}}{\cfrac{1}{R}}$
RLC並列 ・・・ 計算
計算をしてみると、
${P}=IV$
$~~~=I_0 \sin (\omega t + \phi) \times V_0\sin \omega t $
$~~~=I_0V_0 \left( \sin \omega t \cos \phi + \cos \omega t \sin \phi \right ) \sin \omega t \:\cdots\cdots$ 補
$~~~=I_0V_0 \left( \sin^2 \omega t \cos \phi + \sin \omega t \cos \omega t \sin \phi \right ) \:\cdots\cdots$ 補
$~~~=I_0V_0 \left( \dfrac{1-\cos 2 \omega t}{2} \cos\phi + \dfrac{\sin 2 \omega t}{2} \sin \phi \right ) $
時間平均を取るわけだから、 $\cos 2 \omega t = 0 $ $\sin 2 \omega t = 0 $ となる。
これはRLC直列回路の場合と同じ式の形になり、
$\overline{P}=I_0V_0 \dfrac{1}{2} \cos \phi $
$~~~=\dfrac{I_0}{\sqrt{2}}\dfrac{V_0}{\sqrt{2}} \cos \phi $
$~~~=I_e V_e \cos \phi $
RLC並列 ・・・ 図から
コイルとコンデンサーでの消費電力は 0 だから、抵抗だけを考えればよい。
抵抗での消費電力は、
${P}=I_{Re}V_{Re}$ ここで $I_{Re}=\dfrac{V_{Re}}{R}$ より
$~~~=\dfrac{{V_{Re}}^2}{R}$

並列回路のため、各素子にかかる電圧は共通で、 $V_{Re}=V_e$ であるから、
$\overline{P}=\dfrac{{V_{e}}^2}{R}$
また、
抵抗の消費電力のみを考えるわけだから、抵抗に流れる電流 $I_{Re}$ を考え、
図から、 $I_{R0}=I_0 \cos \phi \:\:\cdots\cdots (\ast\ast)$ したがって、 $I_{Re}=I_e \cos \phi$ となります。
( $-\frac{\pi}{2} \leqq \phi \leqq \frac{\pi}{2} $ よって、 $ 0 \leqq \cos \phi \leqq 1$ )
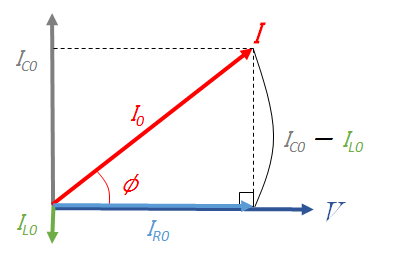
よって、
$\overline{P} = I_{Re}V_{Re} $
$~~~=I_{e}V_{Re} \cos \phi$
並列回路のため、抵抗にかかる電圧は回路全体で共通だから $V_{Re}=V_e$ $V_{R0}=V_0$
$\overline{P}=I_{e}V_e \cos \phi$
RLC並列 ・・・ 力率
力率 $\cos\phi$ については式 $(\ast\ast)$ の $I_{R0}=I_0 \cos \phi$ より、
$\cos \phi=\dfrac{I_{R0}}{I_0}$
$I_0=\dfrac{V_0}{Z}$ $I_{R0}=\dfrac{V_{R0}}{R}=\dfrac{V_{0}}{R}$ だから、
$\cos \phi=\dfrac{ \dfrac{V_{0}}{R} }{\dfrac{V_0}{Z}}=\dfrac{Z}{R}$
RLC直列回路のインピーダンス $Z$ を代入する。$ Z=\dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C – \dfrac{1}{\omega L} \right )^2}} $
$\cos \phi = \dfrac{Z}{R} = \dfrac{\dfrac{1}{R}}{\dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C – \dfrac{1}{\omega L} \right )^2}} }$
$-\dfrac{\pi}{2} \leqq \phi \leqq \dfrac{\pi}{2} $ $ 0 \leqq \cos \phi \leqq 1$
補 三角関数
$\sin(a \pm b)=\sin a \cos b \pm \cos a \sin b$
$\cos(a \pm b)=\cos a \cos b \mp \sin a \sin b$
$a=b$ とすると、
$\sin(a + a)=\sin a \cos a + \cos a \sin a$
$\sin 2a = 2\sin a \cos a$
$\sin a \cos a = \dfrac{\sin 2a}{2}$
$\cos(a + a)=\cos a \cos a – \sin a \sin a$
$\cos2a = \cos^2 a -\sin^2 a$
$~~~~~~=(1 – \sin^2 a) – \sin^2 a$
$~~~~~~=1 – 2\sin^2 a$
$\sin^2 a = \dfrac{1- \cos 2a}{2}$
$\cos2a = \cos^2 a -\sin^2 a$
$~~~~~~ = \cos^2 a -(1 – \cos^2 a) $
$~~~~~~ = 2\cos^2 a -1$
$\cos^2 a =\dfrac{1+\cos 2a}{2}$



































コメント