コンプトン効果・コンプトン散乱
コンプトン効果
コンプトン効果・コンプトン散乱は電磁波であり波動であるはずのX線が、粒子性をもつことの好例です。
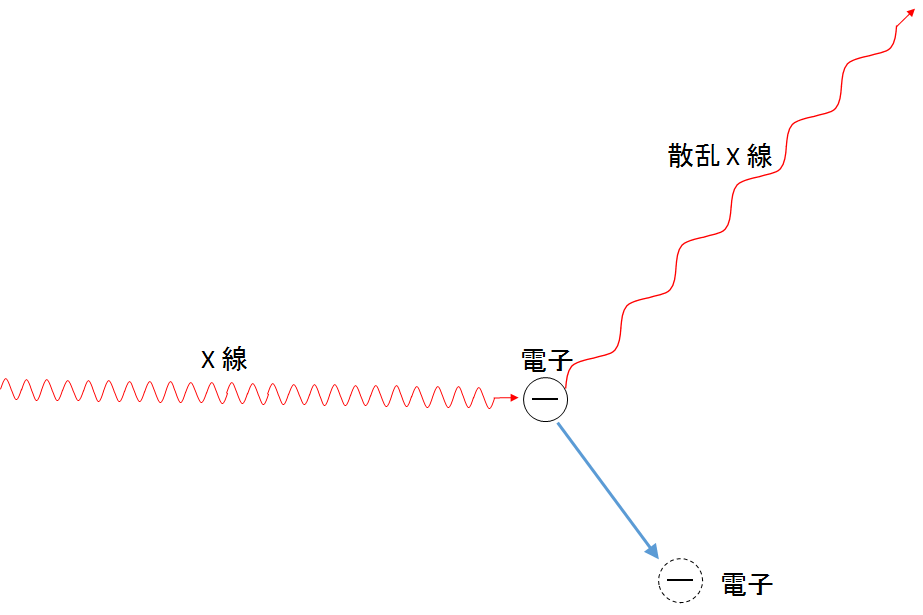
コンプトン効果とは、
「X線を電子に当てた場合、電子によって散乱されたX線の波長がもとのX線の波長よりも長くなる(振動数が小さくなる)」
という現象です。
その波長差 $\lambda^{\prime } – \lambda $ はX線の散乱角を $\phi$ として、以下の式で示されます。
( $m$ 質量 $h$ プランク定数 )$\lambda^{\prime } – \lambda = \dfrac{h}{mc}\left ( 1 – \cos\phi \right )$
コンプトン効果により以下の式、
- 光子のエネルギー $E=h\nu$
- 運動量 $p=\dfrac{E}{c}=\dfrac{h\nu}{c} = \dfrac{h}{\lambda}$
が電磁波であるX線についても成立することが実証されました。
さらに、電磁波は一般に波動性とともに粒子性を持ち、これらの式が成立することがわかっています。
エネルギー:$E$ 運動量:$p$ プランク定数:$h$
光速:$c$ 振動数:$\nu$ 波長:$\lambda$
古典論とコンプトン効果
コンプトン効果・コンプトン散乱は古典物理学では説明できない現象です。
なぜでしょうか。
古典的な波動論では、このような衝突では波の振動数は変化しない・・・というのが通例だからです。
- 例えば、波の単元で学習した固定端・自由端において波が衝突してはね返ってくる場合、波長(振動数も)は変化しません。(もし変化すれば定常波は生じません)
それは波が壁で反射する前後において、同じ媒質で波が伝わるため、波の速度に変化がないからです。波の振動数が変化しない(変化すると1秒間の波の数が合わなくなる)ため、速度変化がないと波長も変化しません。
したがって、衝突後にエネルギーを失うとすれば、波長ではなく振幅が減少していると考えられます。
- もうちょっと原子レベルで考えてみます。
電磁波(X線)がやってきて電子に作用します。
そして、X線の振動数で電子を振動させて、電子が高エネルギー状態になります。
そうすると、電子はその振動数と同じ振動数の波を放出してエネルギーを失う・・・ということになるので、電磁波の速度に変化がないのであれば、X線の作用後に電子から放出される波長はもとのX線と同じになると考えられます。
このように、X線が電子に衝突しても、散乱されたX線の波長は変化しない・・・というのが古典的な波動の考えなのです。
しかし、コンプトン散乱では、「電子で散乱された後のX線波長が長くなる」・・・というわけですから、「コンプトン散乱は古典的波動論では説明できない。」・・・このナゾを解く!、ということですね。

実際にはコンプトン(米 1892-1962)はX線の粒子性を考えて
理論的に散乱X線の波長が長くなることを予測し、
それを実験的に確かめています。
X線の粒子性
電子質量 $m$ として電子とX線に関する衝突は弾性衝突であるとして、エネルギー保存と運動量保存の式をたてます。
ここで、光電効果で出てきた光子エネルギー $E=h\nu=\dfrac{hc}{\lambda}$ と光子運動量 $p=\dfrac{h}{\lambda}$ の関係がX線においても成り立つとし、X線は散乱後の波長 $\lambda^{\prime}$ 、電子の速さ $v$ になったとします。
- エネルギー保存則
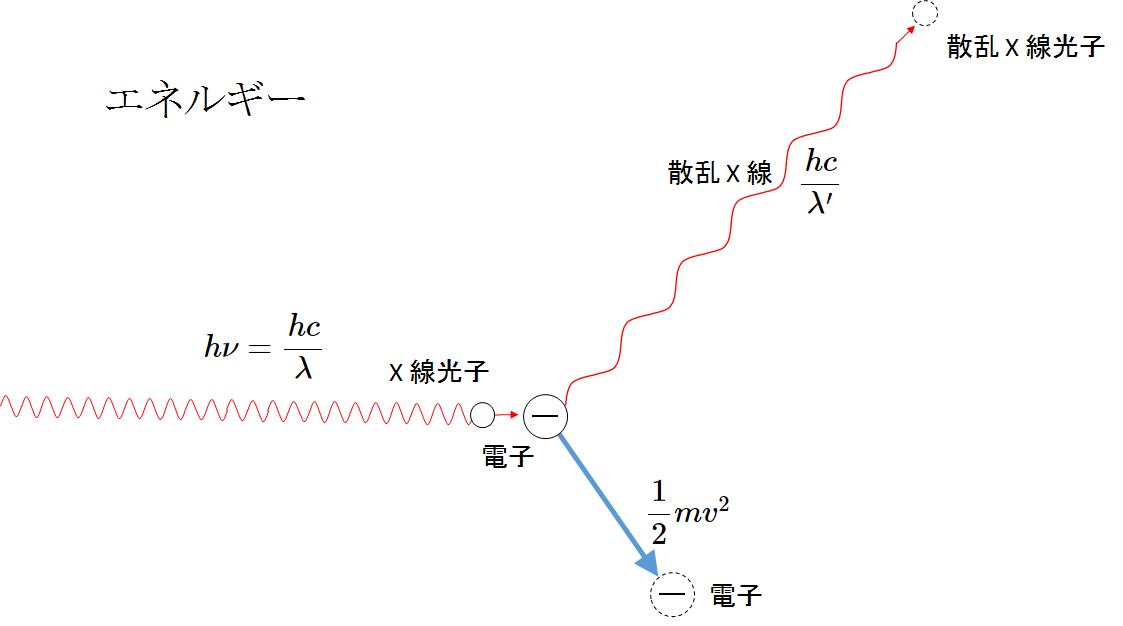
$(h\nu=) \:\: \dfrac{hc}{\lambda}=\dfrac{hc}{\lambda^{\prime}}+\dfrac{1}{2}mv^2\:\cdots\cdots\:(1)$
- 運動量保存則
X線の散乱角を $\phi$ 、電子の跳ね返された角度を $\theta$ とします。
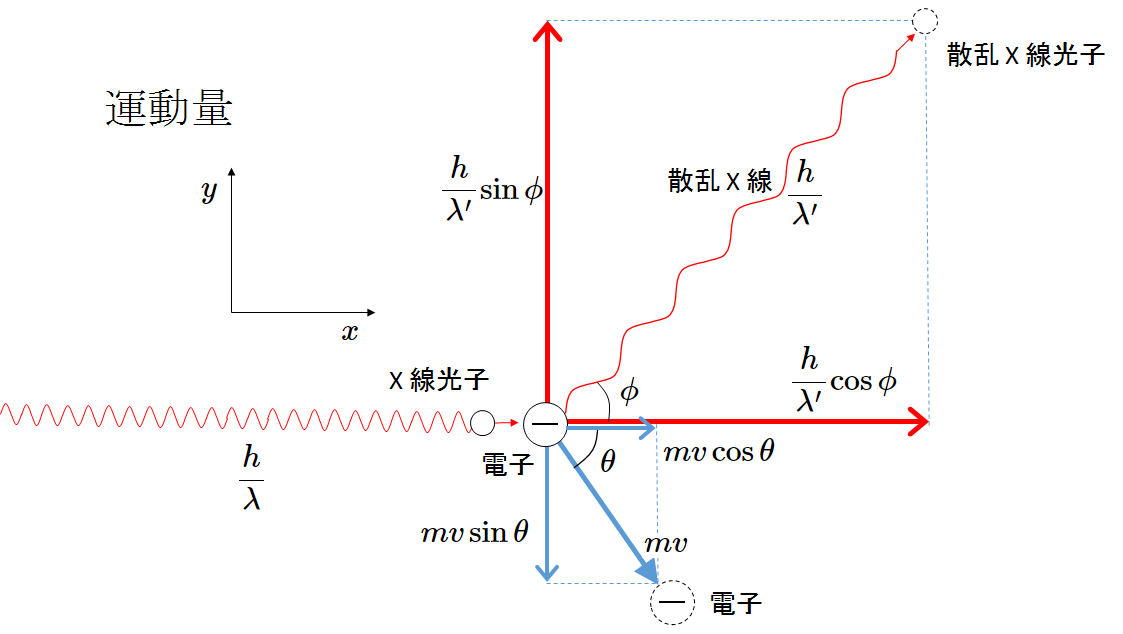
$x$ 軸方向 $\dfrac{h}{\lambda}=\dfrac{h}{\lambda^{\prime}}\cos\phi + mv\cos\theta\:\cdots\cdots\:(2)$
$y$ 軸方向 $0=\dfrac{h}{\lambda^{\prime}}\sin\phi-mv\sin\theta\:\cdots\cdots\:(3)$
これらの式から衝突前後のX線波長の差 $\Delta\lambda=\lambda^{\prime}-\lambda$ を導いていきましょう。
運動量保存の式 $(2)$ より、
$mv\cos\theta = \dfrac{h}{\lambda} – \dfrac{h}{\lambda^{\prime}}\cos\phi $
運動量保存の式 $(3)$ より、
$mv\sin\theta = \dfrac{h}{\lambda^{\prime}}\sin\phi$
これらより、$\sin^2\theta + \cos^2\theta = 1$ の関係から、
$(2)^2 + (3)^2=(mv\sin\theta)^2+(mv\cos\theta)^2 =(mv)^2$
ゆえに、
$(mv)^2 = \left(\dfrac{h}{\lambda^{\prime}}\sin\phi \right)^2+ \left(\dfrac{h}{\lambda} – \dfrac{h}{\lambda^{\prime}}\cos\phi \right)^2$
$ ~~~~~~~~~~ =\left(\dfrac{h}{\lambda^{\prime}}\sin\phi\right)^2 + \left(\dfrac{h}{\lambda}\right)^2 – 2\dfrac{h}{\lambda} \cdot \dfrac{h}{\lambda^{\prime}} \cos\phi + \left(\dfrac{h}{\lambda^{\prime}}\cos\phi\right)^2$
$ ~~~~~~~~~~ =\left(\dfrac{h}{\lambda}\right)^2 +\left(\dfrac{h}{\lambda^{\prime}}\sin\phi\right)^2 + \left(\dfrac{h}{\lambda^{\prime}}\cos\phi\right)^2 – 2\dfrac{h}{\lambda} \cdot \dfrac{h}{\lambda^{\prime}} \cos\phi $
$~~~~~~~~~~ = \left(\dfrac{h}{\lambda}\right)^2+ \left(\dfrac{h}{\lambda^{\prime}}\right)^2 – 2\dfrac{h}{\lambda} \cdot \dfrac{h}{\lambda^{\prime}} \cos\phi $
$~~~~~~~~~~ = h^2\left( \dfrac{1}{\lambda^2} + \dfrac{h}{\lambda^{{\prime}2}} – \dfrac{2}{\lambda\lambda^{\prime}} \cos\phi \right)$
エネルギー保存の $(1)$ 式を、$(mv)^2 =2mhc\left(\dfrac{1}{\lambda} – \dfrac{1}{\lambda^{\prime}}\right)$ と変形して代入します。よって、
$2mhc\left(\dfrac{1}{\lambda} – \dfrac{1}{\lambda^{\prime}}\right)=h^2\left( \dfrac{1}{\lambda^2} + \dfrac{1}{\lambda^{{\prime}2}} – \dfrac{2}{\lambda\lambda^{\prime}} \cos\phi \right) $
$2mhc\left(\dfrac{\lambda^{\prime} – \lambda}{\lambda\lambda^{\prime}} \right) =h^2\left( \dfrac{ \lambda^{\prime 2} + \lambda^2}{ \lambda^2 \lambda^{\prime 2}} – \dfrac{2}{\lambda\lambda^{\prime}} \cos\phi \right) $
上式の両辺に $\lambda\lambda^{\prime}$ をかけます。
$2mhc\left( \lambda^{\prime} – \lambda \right) = h^2\left(\dfrac{ \lambda^{\prime 2} + \lambda^2}{ \lambda \lambda^{\prime}}- 2\cos\phi \right)$
さらに両辺を $2mhc$ で割ります。
$ \lambda^{\prime} – \lambda = \Delta \lambda $
$~~~~~~~~~ = \dfrac{h}{2mc}\left(\dfrac{ \lambda^{\prime 2} + \lambda^2}{ \lambda \lambda^{\prime}}- 2\cos\phi \right)$
ここで $\lambda^{\prime 2}+\lambda^{2}=\left(\lambda^{\prime }-\lambda \right)^2 + 2\lambda\lambda^{\prime }$ と変形します。そうすると、
$ ~~~~~~~~~ = \dfrac{h}{2mc}\left\{\dfrac{ \left(\lambda^{\prime }-\lambda \right)^2 + 2\lambda\lambda^{\prime }}{ \lambda \lambda^{\prime}} – 2\cos\phi \right\}$
$~~~~~~~~~ = \dfrac{h}{2mc}\left\{\dfrac{ (\lambda^{\prime } – \lambda)^2}{ \lambda \lambda^{\prime}} + 2 \: – 2\cos\phi \right\}$
$\Delta \lambda=\lambda^{\prime } – \lambda$ が非常に小さいとき、その2乗値、
$(\Delta \lambda)^2 = (\lambda^{\prime } – \lambda)^2 \fallingdotseq 0 $
が許されるとすれば、
$\lambda^{\prime } – \lambda \fallingdotseq \dfrac{h}{2mc}\left ( 2 – 2\cos\phi \right )$
よってコンプトン効果の式、
$\lambda^{\prime } – \lambda = \dfrac{h}{mc}\left ( 1 – \cos\phi \right )$
を得ることができます。

特にX線の散乱角が $\phi =90^{\circ} $ のとき、 $\cos\phi = 0 $ であるから、
$ \dfrac{h}{mc}\left ( 1 – 0 \right ) = \dfrac{h}{mc}$
$~~~~~~~~~~~~~~= 2.4 \times 10^{-12}\:[m]$
これを(電子の)コンプトン波長 $\lambda$ といいます。
$\lambda= \dfrac{h}{mc}$
この式を眺めてみると質量が長さへと変換されていることがわかります。
以上の理論が実験事実と非常によく一致したため、X線の粒子性が認められ、
- X線光子のエネルギー $E=h\nu$
- X線光子の運動量 $p=\dfrac{E}{c}=\dfrac{h\nu}{c} = \dfrac{h}{\lambda}$
が成立することが実証されました。
さらに、すべての電磁波は一般に波動性とともに粒子性を持ち、これらの式が成立することがわかっています。





































コメント