コンデンサー内に薄い金属板や誘電体を挿入する場合の容量はどうなるでしょうか?
この場合の容量は、挿入した金属板や誘電体はスライドさせても同じです。
なぜでしょうか?一緒に考えていきましょう。
誘電体挿入と電位・電場とグラフについてはこちらをどうぞ!

Fotocitizen / Pixabay
金属板を挿入する
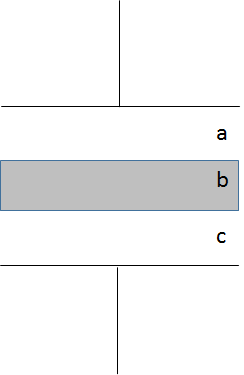
コンデンサーに金属板を挿入する場合ですが、結論としては金属板をコンデンサー内のどこに入れても容量は同じです。
なので、一番計算しやすいところまでスライドさせてください。
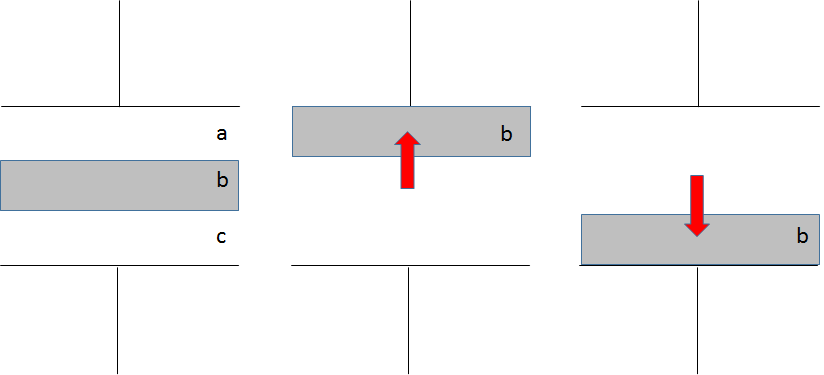
でもなぜでしょうか?
図を見てください。
金属板は太い導線と同じです。
なのでコンデンサー2つの直列とみなせます。

コンデンサーの並列・直列についての記事はこちらへ
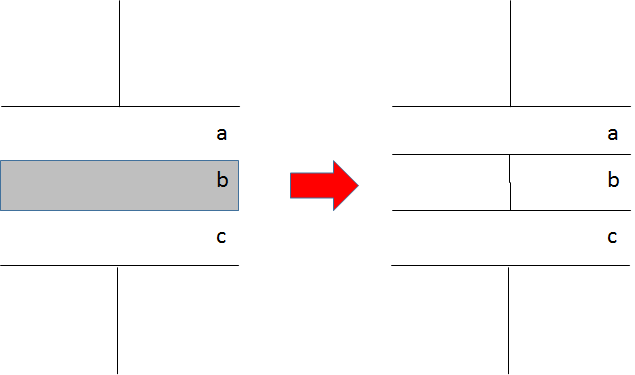
コンデンサー極板の面積を $S$ とし、誘電率を $\epsilon$ としましょう。
$a$ の部分のコンデンサーの容量を$C_a$ 、$c$ の部分の容量を $C_b$ とすると、
\begin{eqnarray}
C_a&=&\epsilon \dfrac{S}{a}\\\\
C_b&=&\epsilon \dfrac{S}{c}\\
\end{eqnarray}
です。
\begin{eqnarray}
\dfrac{1}{C}&=&\dfrac{1}{C_a}+\dfrac{1}{C_b}\\\\
&=&\dfrac{a}{\epsilon S} +\dfrac{c}{\epsilon S}\\
\end{eqnarray}
より、
\begin{eqnarray}
C=\epsilon\dfrac{S}{a+c}
\end{eqnarray}
となります。
ここで $a+c$ はどこへ金属板を移動しても変わらないため、結局金属板をどこへスライドさせても構わないことになります。
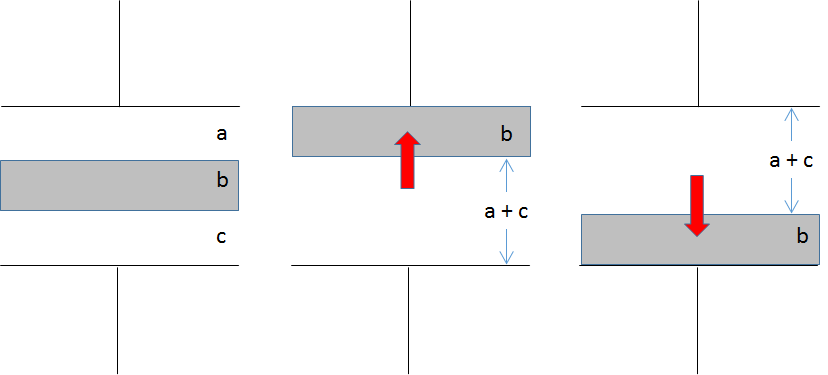
ということは、一番計算しやすい端に移動して計算するのが良いでしょう。
誘電体を挿入する
基本的な考え方は金属板と一緒です。
この場合も、誘電体をどこへスライドさせても大丈夫です。

この場合は誘電体のため次のような直列接続を考えます。
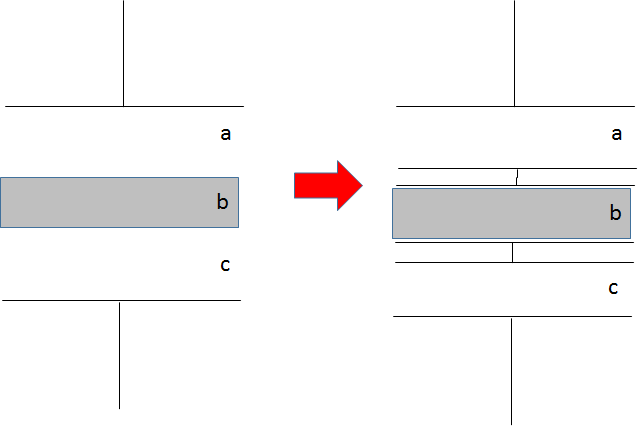
誘電体の比誘電率を $\epsilon_r$ とし、簡単のため他の部分は真空中にあるとします(誘電率 $\epsilon_0 $)。
そうすると、
\begin{eqnarray}
C_a&=&\epsilon_0 \dfrac{S}{a}\\\\
C_b&=&\epsilon_0 \dfrac{S}{b}\\\\
C_c&=&\epsilon_r\epsilon_0 \dfrac{S}{c}\\
\end{eqnarray}
です。
\begin{eqnarray}
\dfrac{1}{C}&=&\dfrac{1}{C_a}+\dfrac{1}{C_b}+\dfrac{1}{C_c}\\\\
&=&\dfrac{a}{\epsilon_0 S} +\dfrac{b}{\epsilon_r\epsilon_0 S}+\dfrac{c}{\epsilon_0 S}\\
\end{eqnarray}
より、
\begin{eqnarray}
C=\epsilon\dfrac{S}{a+c+\dfrac{b}{\epsilon_r}}
\end{eqnarray}
となります。
ここで $a+c$ はどこへ誘電体を移動しても変わらないため、結局誘電体をどこへスライドさせても構わないことになります。

ということはこれもやはりいちばん計算しやすいところまでスライドさせましょう。
こちらもどうぞ







































コメント