物理は原理がわかったつもりでも実際に問題を前にすると考えが思いつかない場合が多いように感じます。
問題に迷ったときは原理原則に立ち返り、丁寧に考える必要があります。
でも人は私も含めて、面倒くさがり屋です。考えるという作業は結構エネルギーを使うのです。
しかし、そこで考えるクセをつけることができた人は難問にも楽しくチャレンジすることができるようなってきます。
コレ本当ですよ。ぜひ実践してください。

Pexels / Pixabay
問題
同じ体積で重さの違うおもり A、B を図のような天秤につるします。
A と B は、いま図の位置でちょうど釣り合っているとしましょう。
これをそのまま水中へ入れましょう。
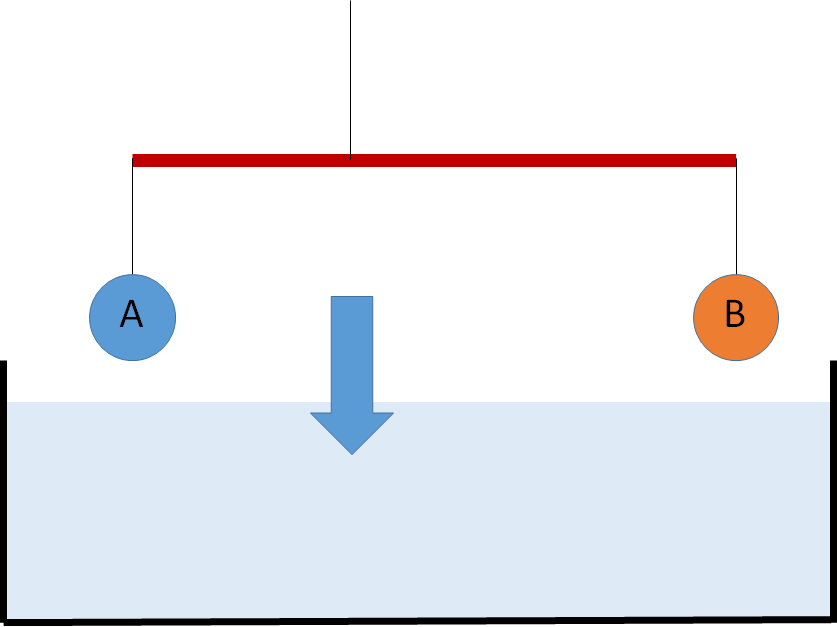
さて A、B はどうなるでしょうか?
- そのまま
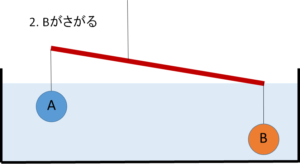
- B がさがる
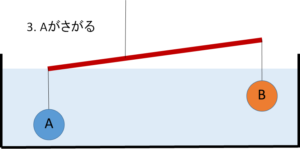
- A がさがる

答えをすぐに求めずに!
さあ!まず考えましょう。
Hint:浮力
now thinking time

PeterKaul / Pixabay
now thinking time
考え方
A とB は重さが違うが体積は同じである。
そのため、浮力は同じだけはたらくことになる。
⇒ アルキメデスの原理:押しのけた流体の重さに等しい浮力がはたらく
簡単に言えば、
水中にある物体を考えたとき、その物体の形をした水を考えます。
そのとき、その水の重さだけの浮力が水中の物体に働くのです。
もっとくだけて言えば、あなたがプールで潜水しているときに受ける浮力はあなたの形をした水の人形を考えて、水人形の重さに等しい浮力を受けるということです。この場合、重要なのは浮力はその物体の体積だけに関係して、物体の重さには無関係であることです。
よくある勘違い
木は軽いから浮力が大きく、鉄は重いから浮力は小さい正
浮力は体積が同じなら同じ大きさだけはたらきます。そして物体の重さには無関係です。木と鉄の体積が同じならばどちらにも同じ大きさの浮力がはたらきます。
この問題の場合 A と B は同体積のため、はたらく浮力は同じです。
いま天秤で釣り合っているということは A のほうが重いことを示しています。
(これはモーメントからそうなります ⇒ A のほうが釣り合い位置まで短いため。シーソーも重たい大人が真ん中に寄りますね)
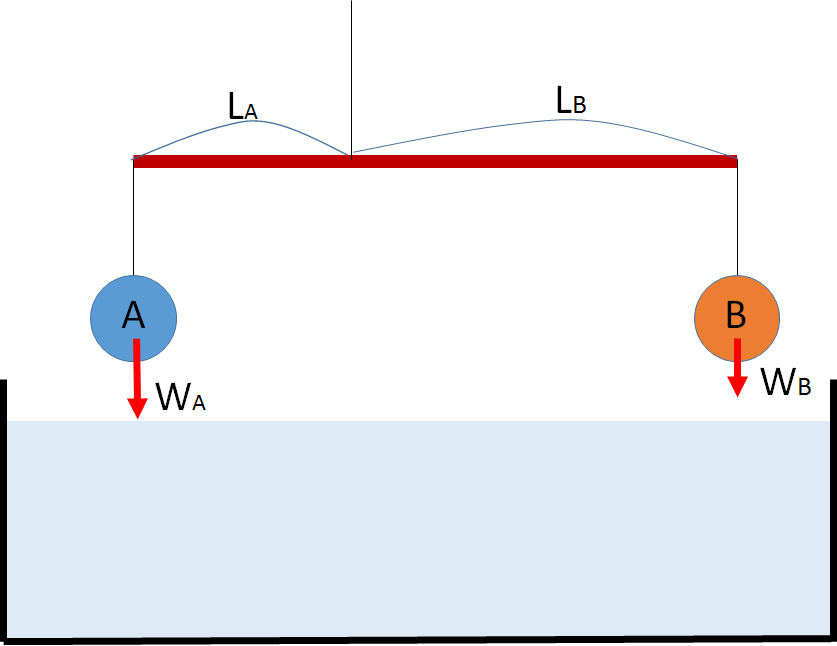
重さは地球が引く力なので水中に入っても変化しません。
しかし、浮力が上向きに働くため、簡単に言えば浮力の分だけ軽くなったと考えてもいいでしょう。
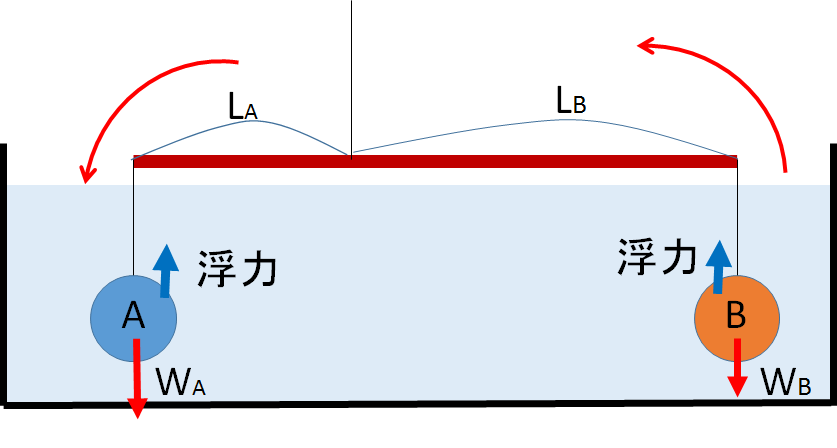
そうすると、A と B はバランスが崩れてしまって釣り合うことができなくなります。
数式で示しましょう。
まず水中にない場合はモーメントの釣り合いから、
$$W_A \times L_A=W_B \times L_B $$
です。次にこれを水中に沈めます。
このとき、浮力を $w$ とすると、まず A に関して、
$(W_A\:-\:w) \times L_A=W_A \times L_A \:-\: w\times L_A $
続いて B に関して
$(W_B\:-\:w) \times L_B=W_B \times L_B \:-\: w\times L_B$
ですね。このとき $W_A \times L_A=W_B \times L_B $ ですから残りは、
$w\times L_A$ と $w\times L_B$ になります。当然、$L_A < L_B$ です。
ということは、$w\times L_A < w\times L_B$ となります。
上の式ではこれを引いているわけですから、B にかかるモーメントが A にかかるそれよりも小さくなります。
その結果 A が下がります。
もっと簡単に!
そんな面倒なことを言わなくても、極端な場合を考えたら明らかです。
重さは A のほうが重く、浮力は A、B ともに同じです。
極端に考えて B の重さと同じだけの浮力が A と B にかかったとしてみればよいのです。
そうすれば、B は水と同じですから浮きも沈みもしないでしょう。
しかし、A は B よりも重いわけですから当然 A が沈んで下がります。








































コメント