コンデンサーのエネルギー

コンデンサーのエネルギー

コンデンサーに充電したとき、コンデンサーはエネルギー $U$ を持ちます。

$U=\dfrac{1}{2}QV=\dfrac{Q^2}{2C}=\dfrac{1}{2}CV^2$

なぜならば、充電したコンデンサーに電球などをつなぐと光ったり、モーターを回したりできるからです。（仕事をすることができる・・・エネルギーがある・・です）

単純な充電回路において、電池の仕事とコンデンサーのエネルギーはイコールになっていません。このことについても考えています。

コンデンサーのエネルギー

このエネルギー $U$ の大きさを求めてみましょう。

力学で学習したように、エネルギーは仕事により増減します。
コンデンサーのエネルギーは電気エネルギーですが、もちろん、エネルギー保存則・エネルギーの原理に従います。

したがって、コンデンサーを充電するための仕事を計算できれば、コンデンサーに蓄えられるエネルギーが計算できるはずです。

ところで、電荷 $q$ を $V$ だけ高いところまで移動 ( 距離 $d$ ) させるときに要する仕事 $W$ は、力を $F$ 、電場 $E$ として、

$W=Fd=qEd=qV$　　$(\:F=qE \: , \:\:\: V=Ed\:)$

です。
あるいは、$+1\:C$ の電荷を $1\:V$ だけ電位が高いところへ運ぶのに要する仕事が $1\:J$ で示されるため、$q$ の電荷を $V$ だけ電位が高いところへ運ぶのに要する仕事が　$W=qV$　である、としてもよいでしょう。

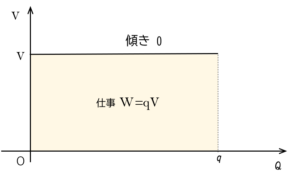
このとき、電圧 $V$ が常に一定だとすれば、この仕事 $W$ は図の四角形の面積で示されます。

次に、電気容量 $C$ のコンデンサーがあるとします。
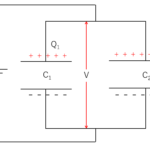
このコンデンサーに電圧 $V$ の電池を接続し、極板間電圧 $V$ になるまで充電します。

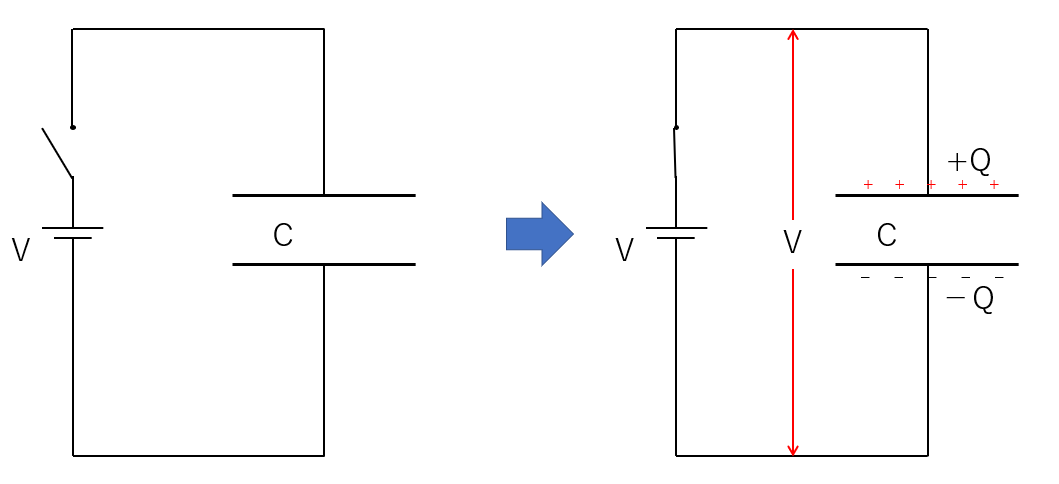
そのとき、最終的にコンデンサーの両端の電圧は電池電圧に等しくなり、充電される電気量は　$Q=CV$　になります。

この式を変形すると、$V=\dfrac{Q}{C}$ となり、コンデンサーの極板間電圧が一定ではなく、$0$ から徐々に大きくなっていくことを示しています。

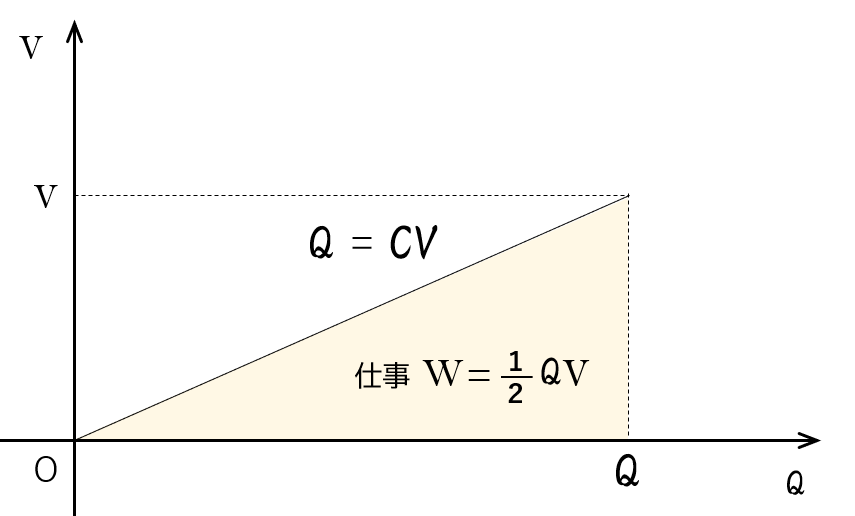
これをグラフに示すと次の図のようになります。$y=ax$ のグラフと同様です。

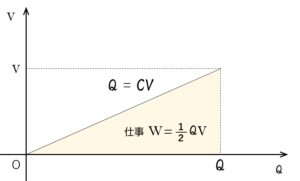
この時のコンデンサーを充電する仕事 $W$ は、図のグラフと横軸の囲む三角形の面積で示されます。

よって、$W=\dfrac{1}{2}QV$　となります。

したがって、この場合のコンデンサーに蓄えられるエネルギー $U$ は

$U=\dfrac{1}{2}QV$

で示されます。

ここで、 $Q=CV$　を用いることでいくつかの式を得ることができます。

$U=\dfrac{1}{2}QV=\dfrac{Q^2}{2C}=\dfrac{1}{2}CV^2$

状況によって、適切な式を使うようにします。

電池による充電のナゾ

この回路において、電池は常に電圧 $V$ を供給しており、電荷 $Q$ を $V$ だけ高い電位まで押し上げています。

それゆえ、コンデンサーが満充電になるまでに電池のした仕事は　$W=QV$　となります。

いっぽう、コンデンサーに蓄えられたエネルギーは、 $U=\dfrac{1}{2}QV$　です。

電池のした仕事の半分しかコンデンサーに蓄えられていません。
残りの半分はどこへ行ってしまったのでしょうか？

この時、残りの半分は、導線の抵抗などでジュール熱として消費された・電磁波として放射された・・などで逃げていったと考えられます。

この場合、電池は律義にずっと電圧 $V$ を供給していた、というのが前提です。

供給電圧が一定である、このような充電の方法である限り、導線の抵抗を減らしても、超電導導線にしても、コンデンサーに蓄えられるエネルギーは　$U=\dfrac{1}{2}QV$　にしかなりません。

そして電池のした仕事の半分は逃げて行ってしまうことになります。

これを防ぐにはどうすればよいでしょうか？
方法としては充電するとき、最初から一定電圧をかけるのではなく、電池電圧をコンデンサー電圧に連動して少しづつ上げていけば、効率は高まるはずです。