エンタルピーについて高校物理の範囲で考えてみました。
高校物理でエンタルピー
熱力学に、エンタルピー $H$ という物理量があります。

言葉の響きがエントロピーと似ていますが、
全くの別概念です。
エンタルピーは、内部エネルギー $U$、圧力 $P$、体積 $V$ とすると、
$$H=U+PV$$
と示されます。
さて、このエンタルピーとやらは何を示しているのでしょうか?
いまここで、気体の状態変化を考えてみます。
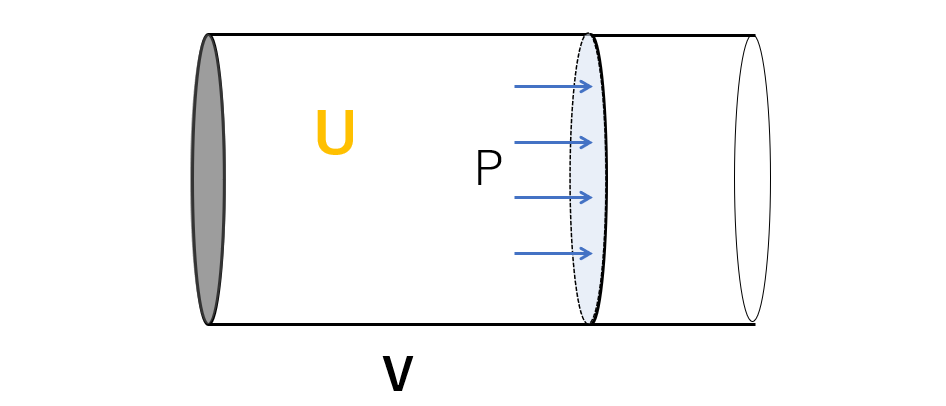
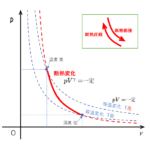
まず、図のように、摩擦なく動くことができるピストンをもつ、注射器のような容器を用意し、中に理想気体を閉じ込めます。
この気体の内部エネルギーを $U$ 、圧力 $P$ 、体積 $V$ とします。
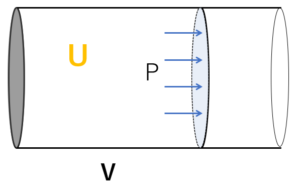
この状態でのエンタルピー $H$ は、$H=U+PV$ となります。
ここで、この容器に外部から熱量 $Q$ を与えることにします。
ピストンは摩擦なく動くため、圧力 $P$ は一定のまま(定圧変化)体積が膨張(収縮)し、 $V’$ になり、内部エネルギーは $U’$ になったとしましょう。
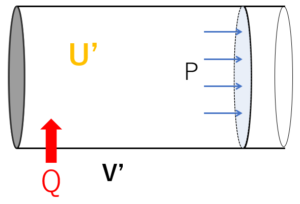
状態変化後のエンタルピーを $H’$ とすると、$H’=U’+PV’$
ここで、これらのエンタルピーの差 $\Delta H$ をとってみます。
そうすると、
\begin{eqnarray}
\Delta H&=&H’-H\\\\
&=&(U’+PV’)-(U+PV)\\\\
&=&(U’-U)+P(V’-V)\\\\
\end{eqnarray}
ここで、 $(U’-U)=\Delta U$、$(V’-V)=\Delta V$ とすると、
$\Delta H=\Delta U+P\Delta V$ となりました。

ここで、熱力学第1法則から
$$Q=\Delta U + W’$$
ここで、$W’$ は気体のする仕事を示しています。
定圧下では、$W’=P\Delta V$ と示されます。
したがって、$Q=\Delta U+P\Delta V$
あれ?
何のことはなく、定圧下では $\Delta H=Q$ となりました。

つまり、エンタルピーの差 $\Delta H$ をとると、
定圧下で、出入りする熱量 $Q$ に等しいということですね。
定圧変化であれば、エンタルピー変化量 $\Delta H$ は、定常状態における内部エネルギーと圧力、そして体積により計算が可能です。
したがって、その時の熱の出入り $Q$ を、エンタルピーを計算することにより得ることができます。
この場合、熱量 $Q$ の定義は、吸収するとき $Q>0$ 、放出するとき $Q<0$ でしたから、エンタルピー $\Delta H$ も、熱の吸収時に$\Delta H>0$、熱の放出時には $\Delta H<0$ となることに注意しましょう。
定積モル比熱と定圧モル比熱
気体の温度が $\Delta T$ だけ上昇したとき、気体の内部エネルギー $\Delta U$ は、$\Delta U=nC_V\Delta T$ で示されますね。($C_V$ は定積モル比熱)
よって、
気体の定積モル比熱は、$C_V=\dfrac{1}{n}\cdot \dfrac{\Delta U}{\Delta T}$ です。
また、気体が定圧変化するときに、温度上昇が $\Delta T$ であったとすると、出入りする熱量 $Q$ は、$Q=nC_P\Delta T$ ですね。
定圧下では、$Q=\Delta H$ でしたから、$Q=\Delta H=nC_P\Delta T$
よって、
気体の定圧モル比熱は $C_P=\dfrac{1}{n}\cdot\dfrac{\Delta H}{\Delta T}$ と表すことができます。




































コメント