物理のエッセンス　力学29番

物理のエッセンス力学29番

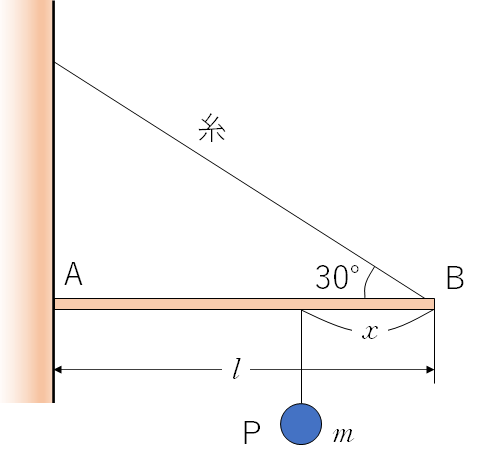
図のような装置で質量 $m$ のおもりPを徐々に左にずらしていくと、Aが滑り出す。

その時の距離 $x$ を求めます。ただし、壁と棒の静止摩擦係数を $\mu$ とします。

解説

題意から、Pを移動させてAが滑り出す直前の状態について考えます。

基本的に剛体の問題の解き方は決まっています。
それは

1. 1. 図を描いて、注目物体にはたらく力をすべてかき入れる。← 最重要
   2. 力のつりあいの式をたてる
   3. ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
   4. 以上の式を連立する

です。

多少の違いはあります（手順2・3などの一部が不要なこともあります）が、基本的にはこのようにすればほとんどの問題の糸口はつかめるはずです。

1.図を描いて、注目物体にはたらく力をすべてかき入れる。

では、図をじっくりと見て、注目物体（ここでは横棒AB）にはたらく力をかき入れていきます。余計な力をかき込まないようにしましょう。

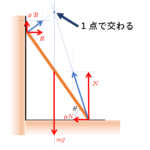
この問題の場合、次の図のような力がかけるはずです。
この力がかけないようであれば、力学の復習をしましょう。

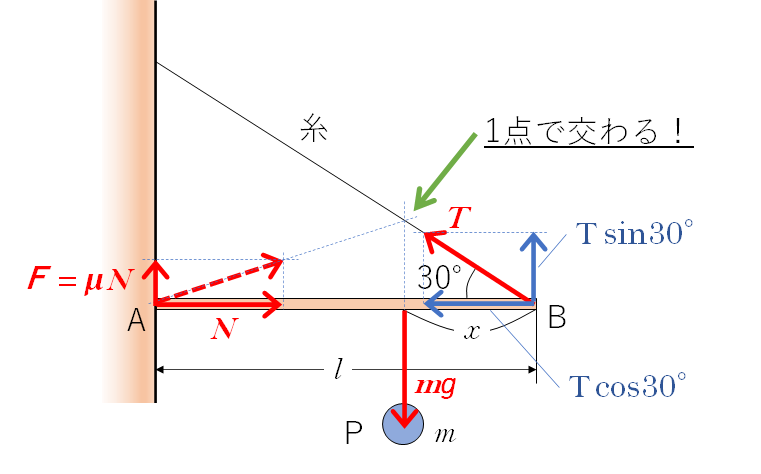
物体は静止しており、これらの力は必ず1点で交わります（上図）。

 

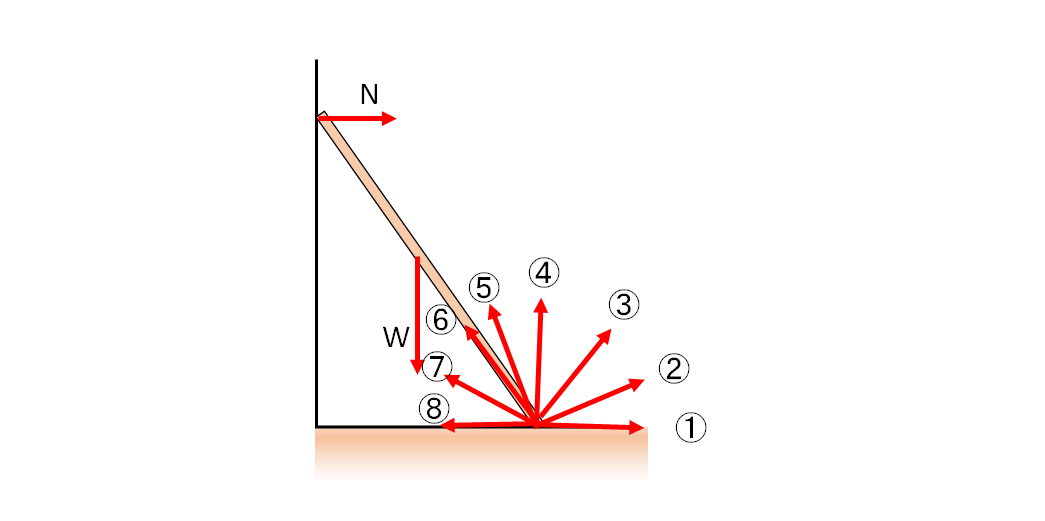
したがってこの問題の場合、壁と棒の摩擦力 $F$ の方向は鉛直上向きになります。

このことについては次の記事を読んでください。

剛体で力を正しく描く　これでもう迷わないたった一つの方法

剛体の作図の際に知っておくべきたった一つのことを伝えます。 これさえ理解できればもう怖くありません。 剛体 剛体は理想的な物体であり、力を受けても変形しません。 世の中の物質で力を受けて変形しないものは存在しないはずです。 しかし、ここでは...

kokolainen.com

2.力のつりあいの式をたてる

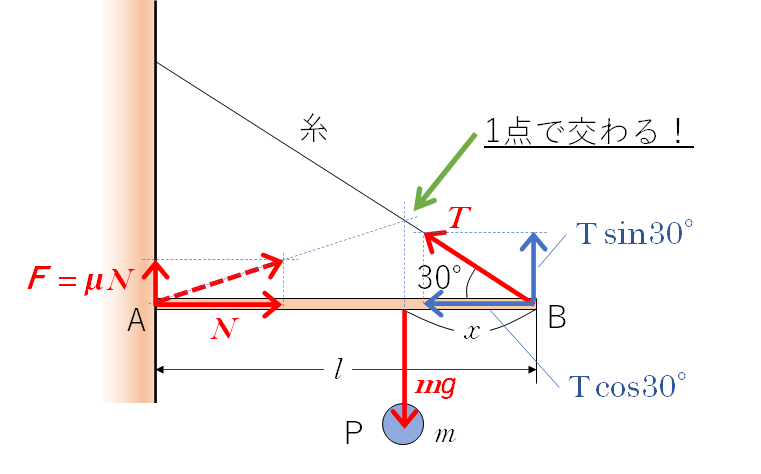
鉛直方向と水平方向に分けてつり合いの式を立てましょう。 注： $F=\mu N$ です。

鉛直方向

$T\sin 30^{\circ}+\mu N=mg\:\:\cdots\cdots \:\mathrm{a}$

水平方向

$N=T \cos 30^{\circ}\:\:\cdots\cdots \:\mathrm{b}$

3.ある点まわりのモーメントの式をたてる

モーメントの式をたてるにあたって、どこを中心にするか決める必要があります。

モーメント中心はどこでもかまいません。
最初にちょっと考えて、都合の良いところにします。

これが納得いかない方はこの記事をお読みください。

剛体で力を正しく描く　これでもう迷わないたった一つの方法

剛体の作図の際に知っておくべきたった一つのことを伝えます。 これさえ理解できればもう怖くありません。 剛体 剛体は理想的な物体であり、力を受けても変形しません。 世の中の物質で力を受けて変形しないものは存在しないはずです。 しかし、ここでは...

kokolainen.com

ここでは B 点まわりを考えることにします。

B 周りにすると T を含む式が消え、簡単になります。
（モーメント中心の選び方は、なるべく式が簡単になるところにします）

B点まわりのモーメントの式

$mgx=\mu Nl\:\:\cdots\cdots \:\mathrm{c}$

4.以上の式を連立する

式 b から、

$T=\dfrac{2N}{\sqrt{3}}$

これを式 a へ代入して

$\dfrac{2N}{\sqrt{3}}\sin 30^{\circ}+\mu N=mg$

$\dfrac{2N}{\sqrt{3}}\dfrac{1}{2}+\mu N=mg$

これを整理して、

$N=\dfrac{\sqrt{3}mg}{1+\sqrt{3}\mu}$

また、式 c より、

$x=\dfrac{\mu N l}{mg}$

ここに先ほどの $N$ を代入して答えを得ます。

$x=\dfrac{\sqrt{3}\mu}{1+\sqrt{3}\mu}l$

動画で解説

以前に作成した動画です。