物理のエッセンス力学 90番 P73

物理のエッセンス力学 90番 P73

物理のエッセンス　力学・波動編　73ページ　90番を参照してください。

動画

問い

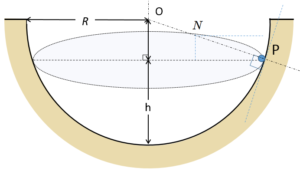
図において、物体にはたらく垂直抗力 $N$ 、速さ $v$、回転の周期 $T$ を求めます。

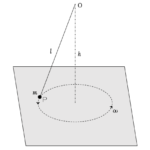
$P$ は図の水平面内で半径 $r$ の等速円運動しています。

答え

ここでは、等速円運動における慣性力である遠心力を考えてみます。

こういった場合、回転系における運動方程式を考えるより、遠心力を考えたほうが馴染みやすいのではないかと思います。

遠心力の方向は回転方向と真逆に $ma$ です。

したがって、遠心力の方向は図の方向（円の中心から遠ざかる方向）で、その大きさは、

$$ma=m\dfrac{v^2}{r}$$

になります。

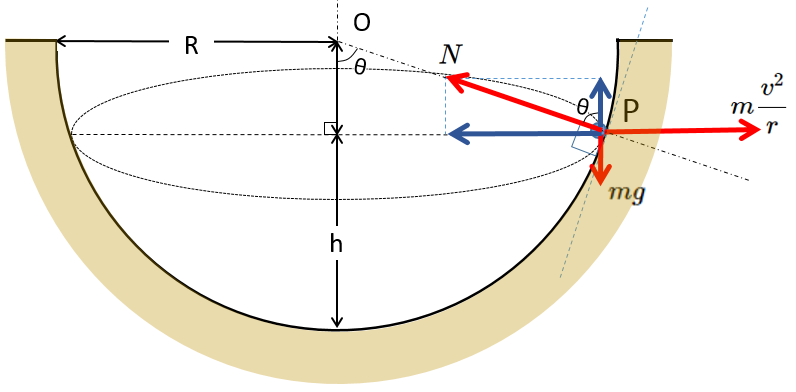
ここで、等速円運動の加速度の式から

\begin{eqnarray}
ma&=&m\dfrac{v^2}{r}\\\\
&=&mr\omega ^2\\\\
&=&mv\omega
\end{eqnarray}

ですね。

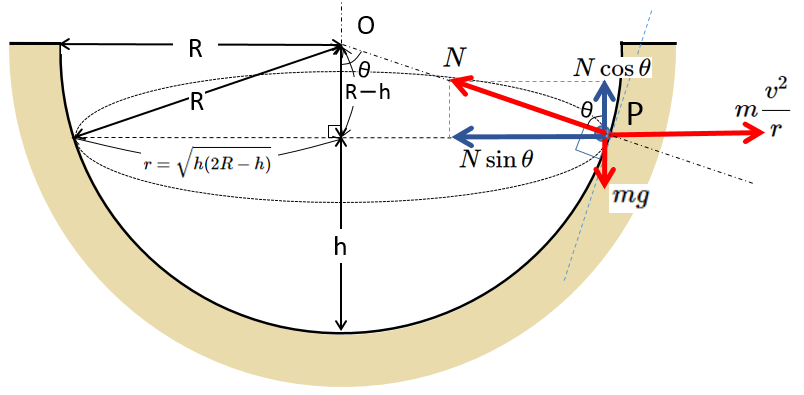
ここでの注意点は半径 $r$ は等速円運動している円の半径です。図より三平方の定理から、

$$R^2=(R-h)^2+r^2$$

すなわち、

$$r=\sqrt{h(2R-h)}$$

となります。

遠心力の大きさは

\begin{eqnarray}
ma&=&m\dfrac{v^2}{r}\\\\
&=&m\dfrac{v^2}{\sqrt{h(2R-h)}}
\end{eqnarray}

また、

$\sin\theta=\dfrac{r}{R}=\dfrac{\sqrt{h(2R-h)}}{R}$

 

$\cos\theta=\dfrac{R-h}{R}$

ここで鉛直方向のつり合いを考えると、

$$N\cos\theta=mg$$

より、

\begin{eqnarray}
N&=&\dfrac{mg}{\cos\theta}\\\\
&=&\dfrac{R}{R-h}mg
\end{eqnarray}

これが垂直抗力 $N$ の大きさを示しています。

さて、水平方向のつり合いは、$N$、$\sin\theta$ の値より

\begin{eqnarray}
N\sin\theta&=&m\dfrac{v^2}{r}\\\\
\left(\dfrac{R}{R-h}mg\right)\left(\dfrac{\sqrt{h(2R-h)}}{R}\right)&=&m\dfrac{v^2}{\sqrt{h(2R-h)}}\\\\
\end{eqnarray}

これより、

$$v=\sqrt{\dfrac{h(2R-h)}{R-h}g}$$

そして、周期 $T$ は、一周 $2\pi r=2\pi \sqrt{h(2R-h)}$ を速さ $v$ で等速円運動するから、

\begin{eqnarray}
T&=&\dfrac{2\pi r}{v}\\\\
&=&\dfrac{2\pi \sqrt{h(2R-h)}}{\sqrt{\frac{h(2R-h)}{R-h}g}}\\\\
&=&2\pi \sqrt{\dfrac{R-h}{g}}
\end{eqnarray}

AmazonAmazonAmazon Amazon