物理のエッセンス力学編 91番 P73
物理のエッセンスの73ページ 91*です。
Amazon
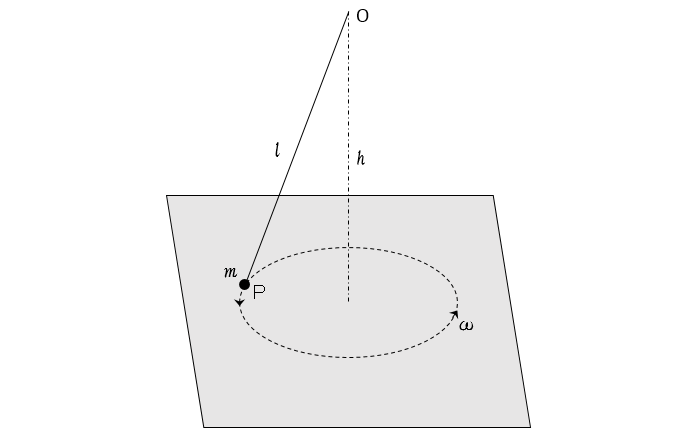
なめらかな水平な床の上での回転運動を考えます。
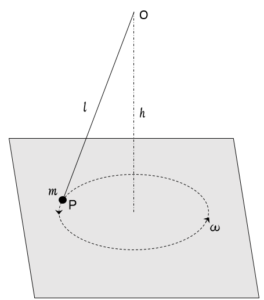
このときの、垂直抗力 $N$ と、質点 P が床から離れるときの角速度 $\omega_0$ を求めます。
考え方

遠心力を考えます。
これは、運動方程式でもいいのですが、個人的には遠心力を考えたほうが間違えにくいとは思っています。
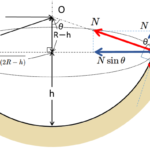
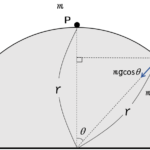
では、力の図を描いてみましょう。
ここでつまづく場合は、もう一度力学の力の復習をしましょう。
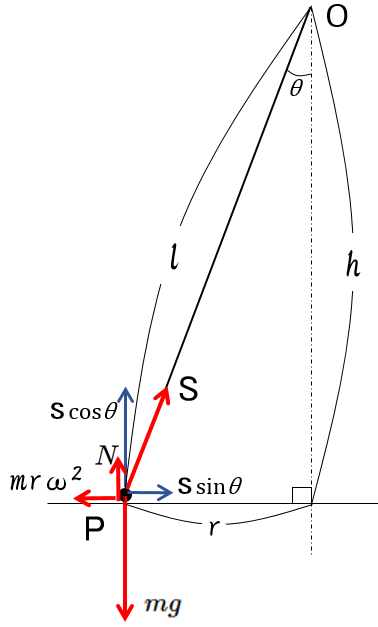
図では遠心力を考えています。

遠心力は慣性力の一種で、円の中心から遠ざかる方向に $ma$ とすればOKです。
この場合、慣性力である遠心力の方向は一定ではなく絶えず変化します。

ここで、等速円運動の加速度の式から
\begin{eqnarray}
ma&=&m\dfrac{v^2}{r}\\\\
&=&mr\omega ^2\\\\
&=&mv\omega
\end{eqnarray}
ですね。
図より、回転半径を $r$ とし、つり合いを考えて、
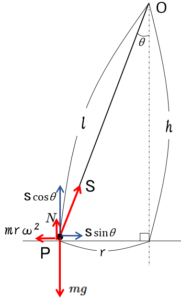
$$S\cos\theta+ N=mg$$
$$S\sin\theta=mr\omega^2$$
が成り立ちます。

注意
このとき、回転半径を $l$ としてしまう間違いが多くあります。
注意しましょう。
ここで、$r^2=l^2-h^2$ だから、$r=\sqrt{l^2-h^2}$
また、三角関数の関係から
$$\sin\theta=\dfrac{\sqrt{l^2-h^2}}{l}$$
$$\cos\theta=\dfrac{h}{l}$$
したがって、
\begin{eqnarray}
S\sin\theta&=&mr\omega^2\\\\
S\dfrac{\sqrt{l^2-h^2}}{l}&=&m\sqrt{l^2-h^2}\omega^2\\\\
S&=&ml\omega^2
\end{eqnarray}
よって、
\begin{eqnarray}
N&=&mg-S\cos\theta\\
&=&mg-ml\omega^2\times \dfrac{h}{l}\\
&=&m(g-h\omega^2)
\end{eqnarray}
$\omega_0$ を求める
床面から離れていれば、垂直抗力 $N=0$ となる。
ゆえに
\begin{eqnarray}
N&=&m(g-h\omega^2_0)=0\\\\
\omega_0&=&\sqrt{\dfrac{g}{h}}
\end{eqnarray}
この、離れるときに垂直抗力などが 0 になるというのは定番ですね。
エッセンスの後は良問、名問がオススメです。
Z会Asteria まずは無料でお試しください



































コメント