物理のエッセンス力学 94番 P77
物理のエッセンスの力学編 94**番 77ページの問題です。
Amazonこのような問題は模試でもよく見ます。
一回やっておけばOKでしょう。
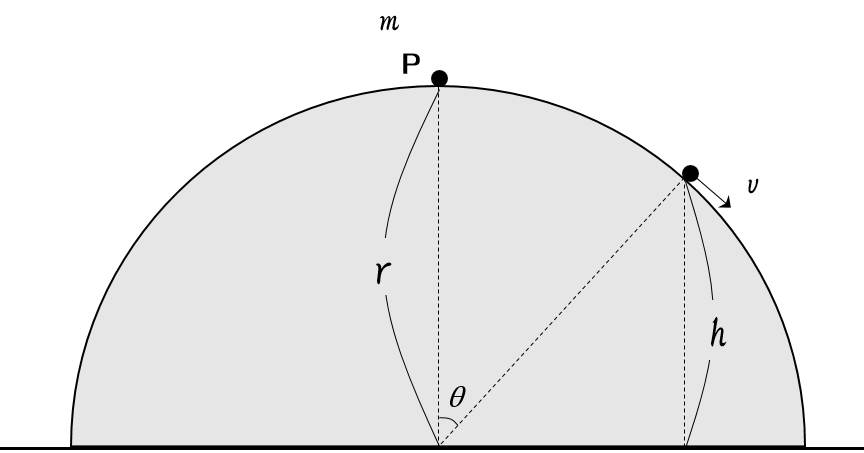
問題は、小物体 P の球面上での速さ $v$ と垂直抗力 $N$ および、球面から離れるときの高さ $h$ を求めるというものです。
解き方
では早速やってみましょう。
速さ $v$
まず質点の速さ $v$ からです。
図の角度 $\theta$ の位置での速さを $v$ とし、エネルギー保存則を立ててみます。
この場合の、エネルギー基準面は角度 $\theta$ の位置の水平面とします。(ご承知のようにどこでも構いませんが)
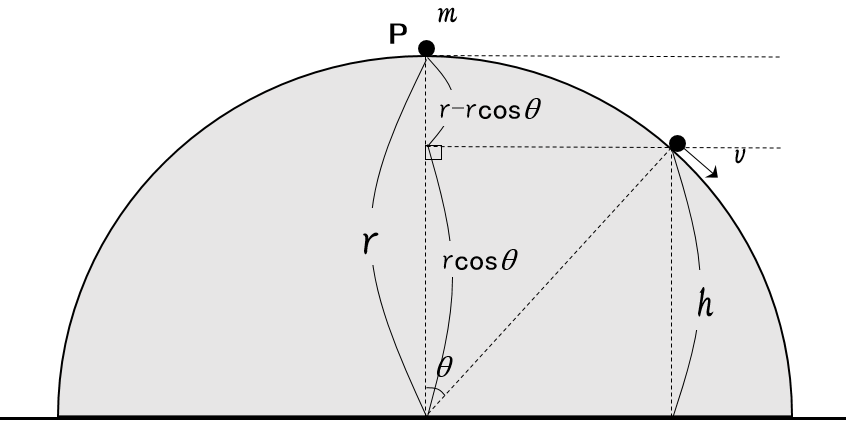
よって、
$$mgr(1-\cos\theta)=\dfrac{1}{2}mv^2$$
$$v=\sqrt{2gr(1-\cos\theta)}$$
です。
垂直抗力 $N$
遠心力 $ma$ を考えた図より、
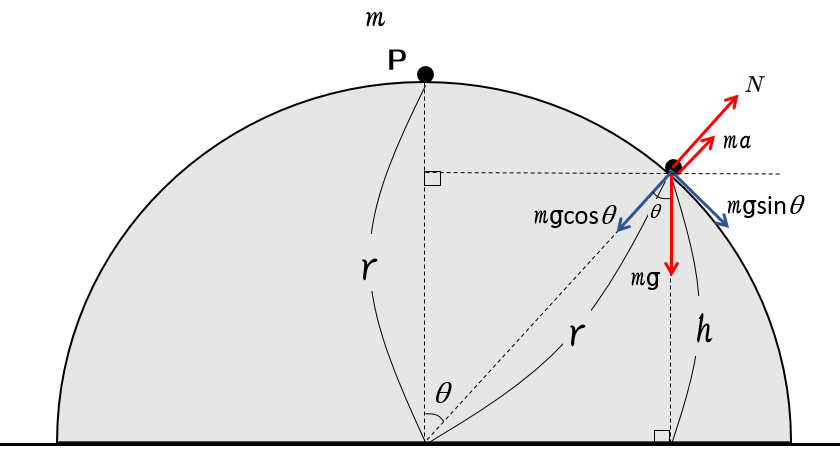
つり合いを考えます。
\begin{eqnarray}
N+ma&=&mg\cos\theta\\\\
N+m\dfrac{v^2}{r}&=&mg\cos\theta\\\\
\end{eqnarray}

このとき垂直抗力 $N$ と慣性力 $ma$ を鉛直と水平方向に分解・・・
してはいけません。
鉛直方向に重力 $mg$、垂直抗力の分力 $N\cos\theta$、慣性力の分力 $ma\cos\theta$ を考えてもつり合っていません。
注意しましょう。
より、$v=\sqrt{2gr(1-\cos\theta)}$ を代入しましょう。
\begin{eqnarray}
N&=&mg\cos\theta-m\dfrac{v^2}{r}\\\\
&=&mg\cos\theta-m\dfrac{2gr(1-\cos\theta)}{r}\\\\
N&=&mg(3\cos\theta-2)
\end{eqnarray}
となります。
球面から離れるときの高さ
よく使う手ですが、面から離れるとき $N=0$ となっていますから、その時の角度 $\theta_0$ とすると、
\begin{eqnarray}
N&=&mg(3\cos\theta_0-2)=0
\end{eqnarray}
より、$3\cos\theta_0-2=0$ です。
したがって、
$$\cos\theta_0=\dfrac{2}{3}$$
$$h=r\cos\theta_0=\dfrac{2}{3}r$$
エッセンスを終えたら良問・名問へと進むのがオススメです。




































コメント