物理のエッセンス力学 101番 P86
物理のエッセンス力学 101番 P86を参照してください。
一見して熱力学?と見える問題ですが、熱力学と単振動の融合問題ですね。
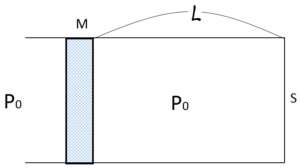
質量 $M$ のピストンで気体を閉じ込めています。
最初は、内部の気体圧力は、大気圧と同じく $P_0$ ですが、$x$ だけ押し込んでパッと離します。
そうするとピストンは単振動を初めます。ただし気体温度は一定とします。
問題は、
-
- ピストンを $x$ だけ押し込んだときの内部の気体の圧力
- 単振動の周期
を求めることです。
やってみよう
動画解説
1
まず1から。
これは純粋に熱力学の問題ですね。
ピストンを $x$ だけ押し込んだときの内部の気体圧力を求めます。
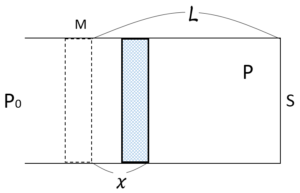
ボイル・シャルルの法則を使いましょう。

気体圧力 $P_0\rightarrow P$、気体体積 $V_0\rightarrow V$ ,
、気体温度 $T_0\rightarrow T$ のとき、
ボイル・シャルルの法則とは
$$\dfrac{P_0V_0}{T_0}=\dfrac{PV}{T}$$
ですね。
この問題の場合は気体の温度一定ですから、
$${P_0V_0}={PV}$$
問題において、ピストンを $x$ 押し込んだときの圧力を $P$ とすると、
$$P_0(SL)=P\{S(L-x)\}$$
より、
$$P=\dfrac{SL}{S(L-x)}P_0=\dfrac{L}{L-x}P_0$$
$$P=\dfrac{L}{L-x}P_0$$
です。
2
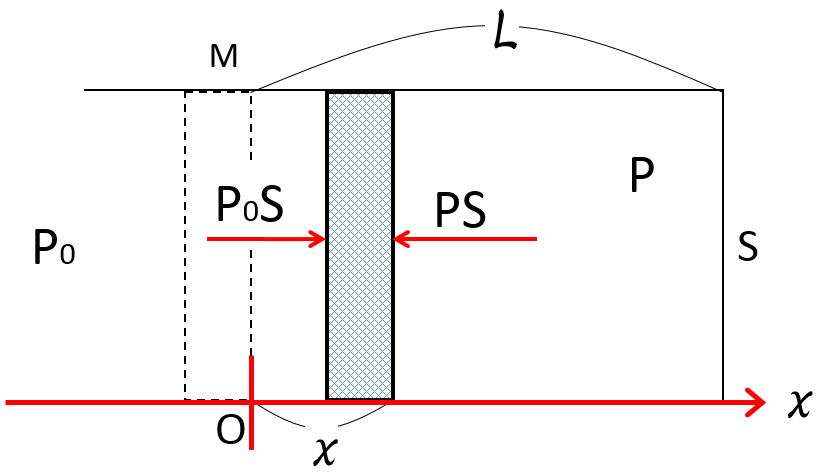
ピストンを $x$ だけ押し込んだときの力の様子を図に表してみましょう。
力学なので力を描けることが非常に重要です。
注:鉛直方向の力は省略しました。
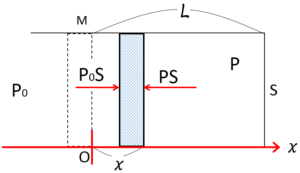
このとき、1 より $P=\dfrac{L}{L-x}P_0$ だったから、ピストンにはたらく合力 $F$ はこの場合は、図のように $x$ 軸を取ると、
\begin{eqnarray}
F=P_0S-PS&=&P_0S-\dfrac{L}{L-x}P_0S\\\\
&=&P_0S(1-\dfrac{L}{L-x})\\\\
&=&P_0S\dfrac{-x}{L-x}
\end{eqnarray}
となります。

このとき、単振動する条件を思い出してみましょう。
それは復元力がはたらくことです。
復元力 $f$ とは、$f=-kx$ のような力を意味しています。
さて、いま出した合力 $F$ は
\begin{eqnarray}
F&=&P_0S\dfrac{-x}{L-x}\\\\
&=&-\left(\dfrac{x}{L-x}\right)P_0S\\\\
\end{eqnarray}
です。

つまり、$f=-kx$ のような力の形にしたいのです。
右辺の分母において $L$ でくくると、
\begin{eqnarray}
F&=&-\left(\dfrac{x}{L-x}\right)P_0S\\\\
&=&-\dfrac{x}{L(1-\dfrac{x}{L})}P_0S\\\\
\end{eqnarray}
ここで問題文から、$ |x|\ll L $ なので、$ \dfrac{|x|}{L}\ll 1 $
$$1-\dfrac{x}{L}\fallingdotseq 1$$
を考えて、
\begin{eqnarray}
F&=&-\dfrac{x}{L(1-\dfrac{x}{L})}P_0S\\\\
F&\fallingdotseq &-\dfrac{P_0S}{L}x\\\\
&=&-kx
\end{eqnarray}
よって、ピストンは単振動することがわかります。
ただし、$k=\dfrac{P_0S}{L}$
ゆえに、単振動の周期の式 $T=2\pi\sqrt{\dfrac{m}{k}}$ より、
\begin{eqnarray}
T&=&2\pi\sqrt{\dfrac{M}{k}}\\\\
&=&2\pi\sqrt{\dfrac{ML}{P_0S}}\\\\
\end{eqnarray}
近似の疑問

このとき、たとえば、
\begin{eqnarray}
F&=&-\left(\dfrac{x}{L-x}\right)P_0S\\\\
&=&-\dfrac{\dfrac{x}{L}}{1-\dfrac{x}{L}}P_0S\\\\
\end{eqnarray}
と考えれば、$\dfrac{x}{L}\fallingdotseq 0$ として、
$F\fallingdotseq 0$ とは考えられないのですか?

そうですね。そうなるような気もしますが、
この場合、$F\fallingdotseq 0$ としてはいけません。
なぜなら、$\dfrac{x}{L} \ll 1$ のとき、まあ $0.00001$ とでもしましょう。
次に、$P_0S$ にとても大きい数を想像してください。
$6.0\times 10^{23}$ とか・・・。
そうなると、$1-\dfrac{x}{L}$ は計算上 $1$ としても差し支えありませんが、
$\dfrac{x}{L}P_0S$ を $0$ とするのはダメだとわかるでしょう?


エッセンスの後は良問・名問がオススメです。





































コメント