相対速度　物理のエッセンス 力学 13番

相対速度　物理のエッセンス 力学編 13番

相対速度の考え方から始めて、物理のエッセンスの力学編 13番　を考えてみましょう。

相対速度

一般的に「速度」といった場合の考え方

一般的に単に「速度」といった場合の考え方は、「静止系から見て観測した速度」のことを指します。

例えば、観測者が静止した地面に立ち、運動している物体を観測する・・というような具合です。

地表も、地球が運動していることを考えれば静止系ではありませんし、慣性系でもありません（回転している）。

 

一般に、宇宙空間にも絶対静止空間はない、とされていますが、ここでは便宜的に、地表面を静止系と考えます。

 

相対速度の考え方

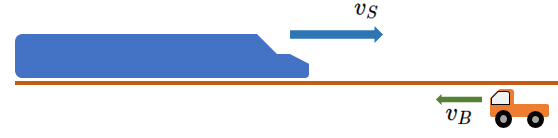
では、運動している物体から観測した場合はどのようになるのでしょうか？

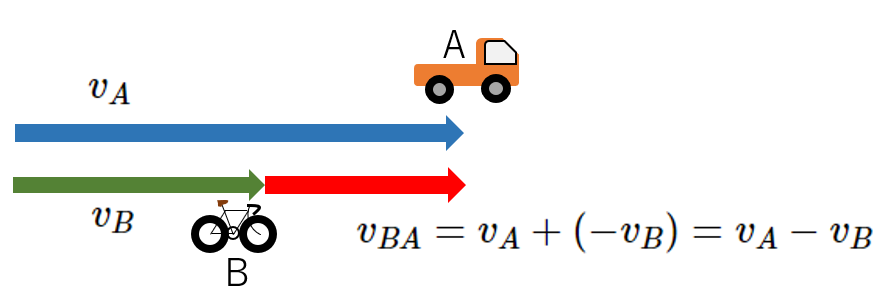
図では、自転車と自動車はともに、等速直線運動しているとしましょう。
A : Automobile      B : Bycycle   の略です。

この場合、地表で停止している人が見ると、当然、自動車の速度は $v_{A}$ です。

今度は、自転車（ 速度 $v_B$ ）に乗って観測します。

先ほどの考え方を適用すると・・・

「自転車の人から見て、自動車は　（－自転車の速度）　で運動しているように見える」でしたから、　

$$自転車から見た自動車の速度 = (自動車の速度)+ (-自転車の速度)$$

すなわち、

$$v_{BA}=v_A+(-v_B)=v_A-v_B$$

とすればよいのです。

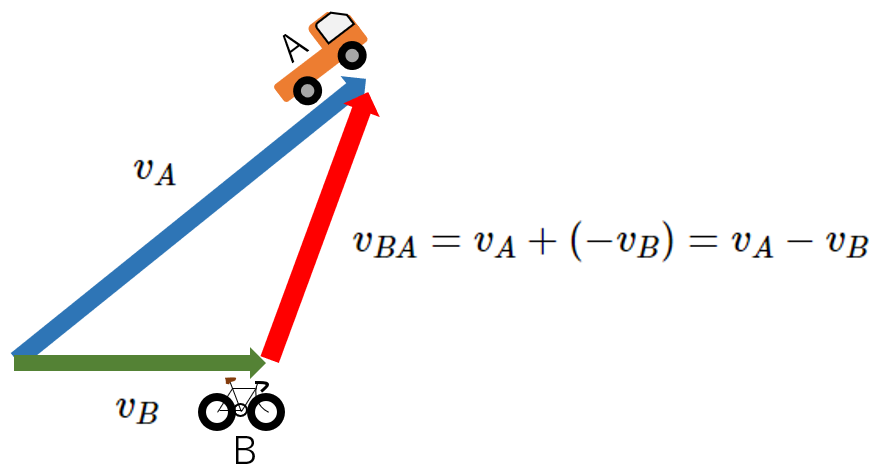
また、速度はベクトル量のため、ベクトル的な考え方をすれば、どのような場合も簡単に作図できます。

相対速度ベクトルは、見るほうから見られるほうへ、ベクトルの矢印を引けばよいのです。

$$\vec{v_{BA}}=\vec{v_A}+(-\vec{v_B})=\vec{v_A}-\vec{v_B}$$

直線状の時

2次元の時

この辺りは以前の記事を参照してください。

相対速度のうまい方法

相対速度はわかってしまえばどうということはないのですが、ちょっと戸惑う概念です。 この記事で相対速度についてしっかり理解してくださいね。 もう間違えない！いい方法もお教えします。

kokolainen.com

問題13番を解いてみた

新幹線の速さ $v_S=198\:\mathrm{km/h}=55\:\mathrm{m/s}$ 、自動車 A ・B の速さはともに、 $v_A=v_B=90\:\mathrm{km/h}=25\:\mathrm{m/s}$ です。
また、新幹線の長さは $480\:\mathrm{m}$ で、自動車の長さは無視できます。

自動車 A・Bと新幹線がすれ違う時の所要時間を計算しよう・・というのが問題です。

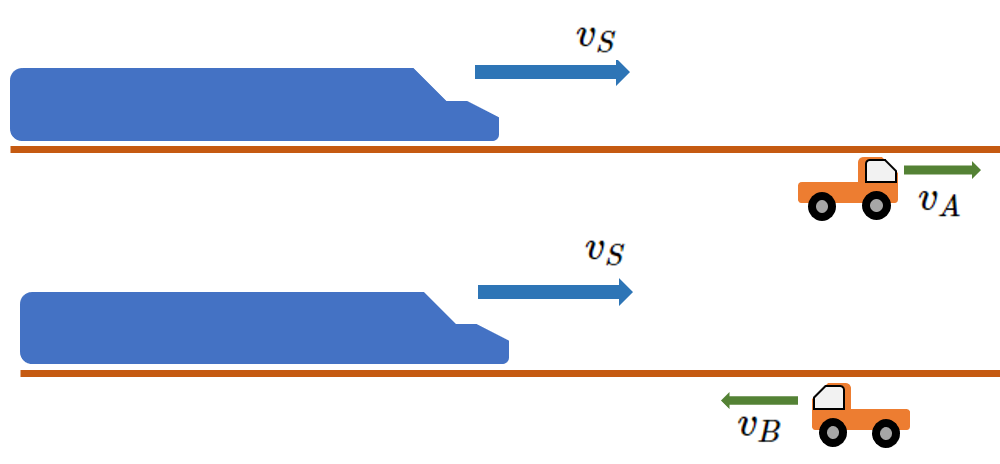
自動車Aが新幹線と同方向に走る場合

新幹線から自動車を見た時の、相対速度 $v_{SA}$を考えます。

自動車から見た新幹線を考えても構いません。

式から考える

右向きを正と考えると、$v_S=55\:\mathrm{m/s}$、$v_A=25\:\mathrm{m/s}$　です。

$v_{SA}=v_A-v_S=25+(-55)=-30\:\mathrm{m/s}$

ベクトル図から考える

新幹線から自動車を見るのですから、ベクトル図で新幹線のベクトルの頭から、自動車の速度ベクトルの頭へ矢印を引きましょう。

それが、新幹線に対する自動車の相対速度ベクトルです。

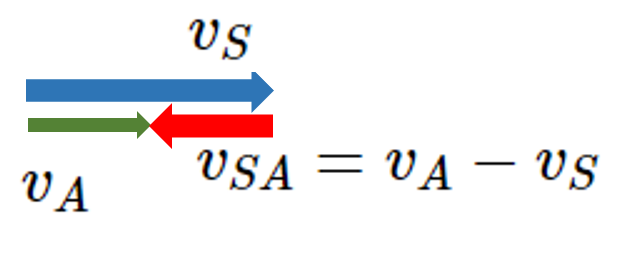
図から相対速度ベクトルの大きさを計算して用います。

この場合、新幹線が静止していると考えて構いません。
新幹線に乗っている人から見ると、停まっている新幹線に対して、自動車Aが $30\:\mathrm{m/s}$ でバックしてくるように見えます。

そして、新幹線の先頭を通過して、やがて最後尾に到達します。
したがって、自動車が、新幹線の先端部から最後尾まですすむのにかかる時間を計算すればよく、

$$時間 t =\dfrac{距離 x}{速さ v}=\dfrac{480}{30}=16 \:\mathrm{s}$$

となります。

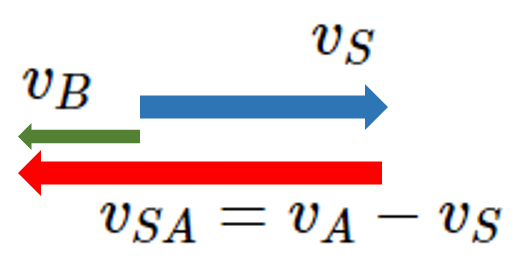
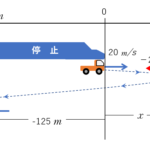
自動車Bが新幹線と反対方向に走る場合

同様に、新幹線から見た相対速度 $v_{SA}$を考えます。

式から考える

右向きを正と考えると、$v_S=55\:\mathrm{m/s}$、$v_B=-25\:\mathrm{m/s}$　です。

$$v_{SA}=v_A-v_S=(-25)+(-55)=-80\:\mathrm{m/s}$$

ベクトル図から考える

新幹線から自動車を見るのですから、ベクトル図で新幹線のベクトルの頭から、自動車の速度ベクトルの頭へ矢印を引きましょう。

それが、新幹線に対する自動車の相対速度ベクトルです。

図から相対速度ベクトルの大きさを計算して用います。

この場合も、新幹線が静止していると考えて構いません。
新幹線に乗っている人から見ると、停まっている新幹線に対して、自動車Bが $80\:\mathrm{m/s}$ で突っ込んでくるように見えます。

そして、新幹線の先頭を通過して、やがて最後尾に到達します。
したがって、自動車が、新幹線の先端部から最後尾まですすむのにかかる時間を計算すればよく、

$$時間 t =\dfrac{距離 x}{速さ v}=\dfrac{480}{80}=6.0 \:\mathrm{s}$$

となります。

注：ともに、相対速度の大きさで時間を計算しましたので、

速度の絶対値をとっています。