物理の問題を解くときに、「こういう設定でお願いね」というのがあって、例えばそれは「摩擦なし」だとか「空気抵抗なし」だとかがありますね。
そういったものの一つに「張力はどこでも同じとします」というのがあって、「なぜ一緒なんだ?」と心のどこかで疑問に思いつつも、そういったもの・・・・とスルーしてしまうことってありますよね。
どうして張力ってどこでも一緒なんでしょうか?
この記事ではその疑問にまじめに答えます。
張力
物理で出てくる力の一つに張力というものがあります。
糸の引く力ですね。
普通は T とか S で表されます。
教科書や参考書を見ていると、一様に「張力はどこでも一定とする」というような記述が見られます。
あるいは、「糸が軽いとき」と記述があるときは、何も言わずとも張力はどこでも同じとして扱われるのが一般的です。
でもどうして、糸が軽いと張力がどこでも一緒になるのでしょうか?
どう思いますか。
そんなこと考えたこともなかった・・かもしれません。
でもこういう素朴な疑問って大切だと思いませんか?
運動方程式
図で考えていきましょう。
質量 $m$ と、$M$ の物体が糸でつながれています。
この状態で 一方の物体を力 $F$ で引いてやることにします。
図で糸の張力 $T$、$T’$ としましょう。
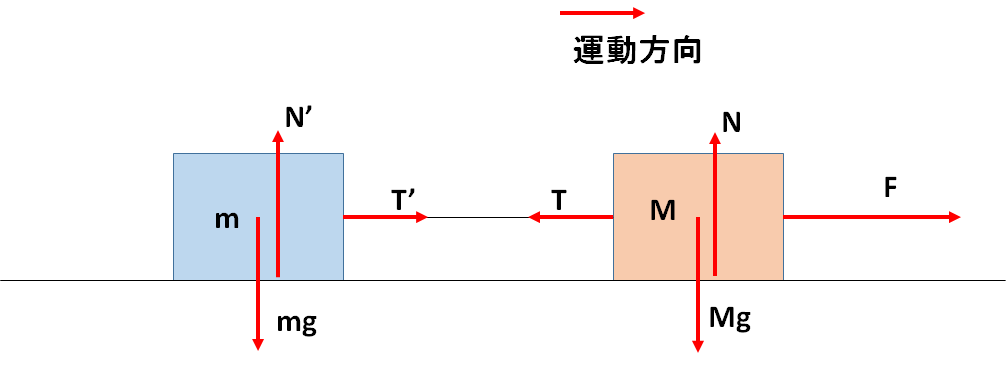
図では、質量 $M$ の物体、質量 $m$ の物体、そして糸は図の右側へ加速度 $a$ で運動しています。
運動方程式 $ma = F$ に従えば、皆さんおなじみの式
$M$ について
$$Ma = F - T$$
$m$ について
$$ma = T’$$
となりますね。
しかし、いまは糸についても考えています。
糸も図の右へ加速度 $a$ で運動しているのです。そこで、糸の質量を $m’$ としましょう。
$T$ と $T’$ の作用反作用を考えて、糸にはたらく水平方向の力は次の図のようになります。
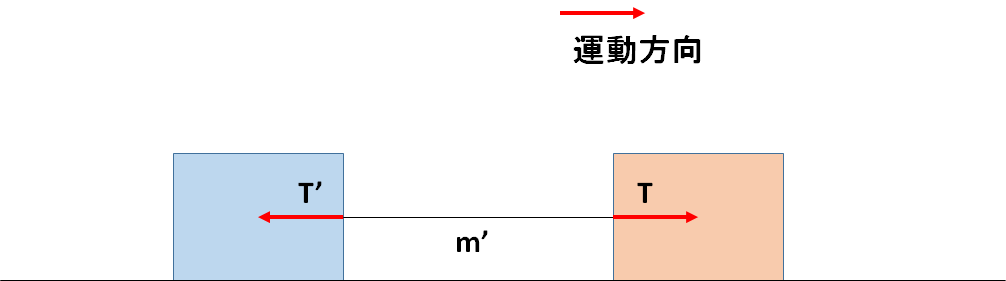
糸についての運動方程式は
$$m’a = T - T’$$
となります。
ここで、「糸が軽い」ということを思い出してください。
すなわち、$m’ \simeq 0$ なのです。注意:$a$ は $0$ ではありません。
したがって、
$$m’a = 0 = T- T’$$
より、$T’ = T$ となるのです。
もし糸の質量だって無視できないのであれば張力は当然
$T > T’$
となります。
動画解説
糸の張力が一様とならない場合の問題の解説を動画でしています。参考にしてください。
物理のエッセンスの力学編 問題番号 46 です。





































コメント