キルヒホッフの法則

キルヒホッフの法則

複雑な回路をどう考えるべきか？
キルヒホッフの法則（キルヒホフの法則）がその答えになります。

例えば、図のような回路においてキルヒホッフの法則は次のように表現されます。

キルヒホッフの法則

• キルヒホッフの第1法則
  回路中の交点について、流れ込む電流和＝流れ出る電流和
• キルヒホッフの第2法則
  任意の閉回路において、起電力の和＝電圧降下の和  $\sum E=\sum RI$

それぞれについて詳しく見ていきましょう。

キルヒホッフの第1法則

キルヒホッフの第1法則
回路中の交点について、流れ込む電流和＝流れ出る電流和

回路の交点には、電気をためる機能はありません。

したがって、交点において、流れ込む電流の和が流れ出る電流の和に等しい、が成り立ちます。

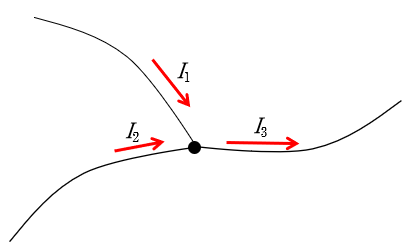
図では、$I_1+I_2=I_3$　が成り立ちます。

あるいは、交点に流れ込む電流を正、流れ出る電流を負、とすると、

$I_1+I_2-I_3=0$

のように書いても同じことです。

電流の向きがあらかじめわからないときは、適当に電流の向きを仮定します。

その際、もし次の図のように仮定してしまったとしましょう。

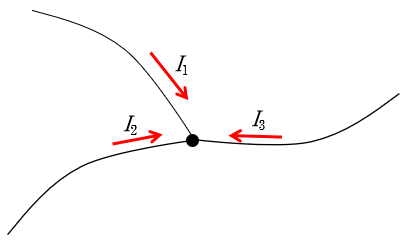
実際にはこのように電流が流れることはあり得ません。

しかし、流れ込む電流を正として、$I_1+I_2+I_3=0$　とすれば答えはちゃんと出ます。

そして、答えの電流の値が負であった場合、仮定と逆向きである、ということです。

キルヒホッフの第2法則

キルヒホッフの第2法則
任意の閉回路において、起電力の和＝電圧降下の和  $\sum E=\sum (RI)$

閉回路とは、一回りの閉じた回路を指します。

電池は電位を上げます。そして抵抗では電圧「降下」するため、

一回りして元のところへ戻るのであれば、当然、

「上がる分=下がる分」、つまり、 $\sum E=\sum RI$　

となるはずです。

 

哲学の本か何かで読んだ

「上り坂と同じ数だけ下り坂がある」

とよく似ている？

では、図の回路を使って考えましょう。

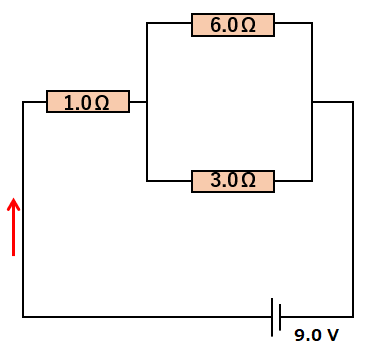
任意の閉回路を決めます。

図では、複数の閉回路を考えることができます。

基本的には、以下の図にあるように、どの閉回路（オレンジの線）を考えてもOKです。

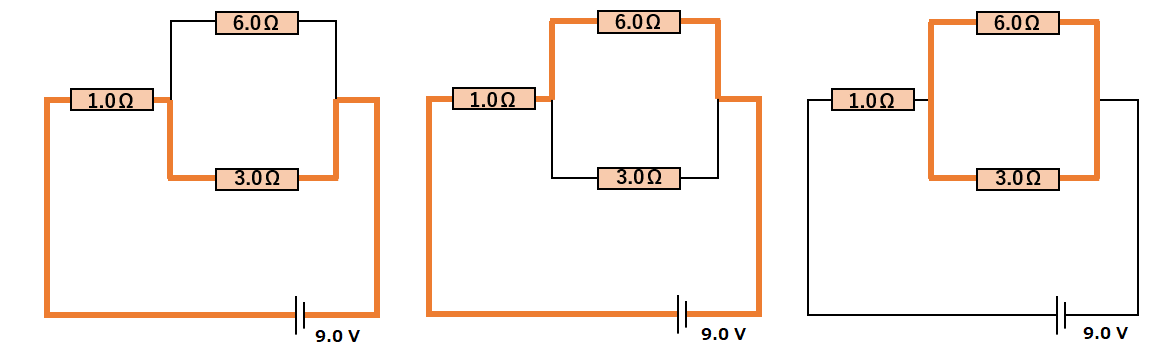
次に、考える閉回路の回る向きを決めます（図参照してください）。
これも原則、どのように決めても構いません。

そして、電圧降下が起こる箇所（この回路では抵抗部分だけです）を流れる電流を仮定します。

このとき、電流の流れる方向も、自由に決めて大丈夫です。
ただし、途中で変更してはいけません。
間違えないように図に書きいれておきます。

それでは、今回は図の青い矢印の向き（時計回り）に回ると決めます。
そして、電流の向きと大きさをそれぞれの抵抗の部分で、図の $I_1,\:I_2,\:I_3$ のように仮定します。

方程式を解く

では、方程式を立ててみましょう。

まず、キルヒホッフの第1法則ですが、交点を1つ考えてみます。（どこでもかまいません）
そうすると、

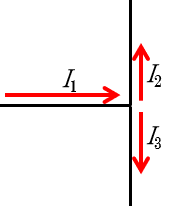
図より、　$I_1=I_2+I_3$　　または　　$I_1-I_2-I_3=0$ 　　です。

次の図から、閉回路に沿って、$\sum E=\sum RI$　を考えると、

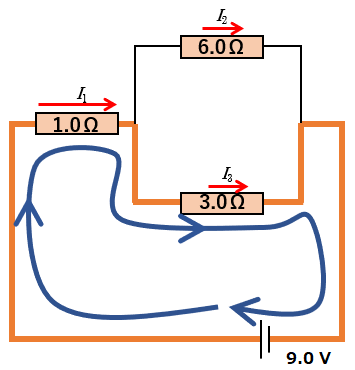
$9.0=1.0\times I_1+3.0\times I_3\:\:\cdots (1)$

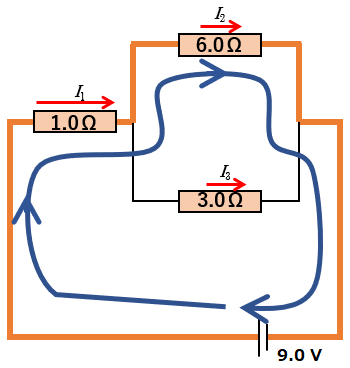
$9.0=1.0\times I_1+6.0\times I_2\:\:\cdots (2)$

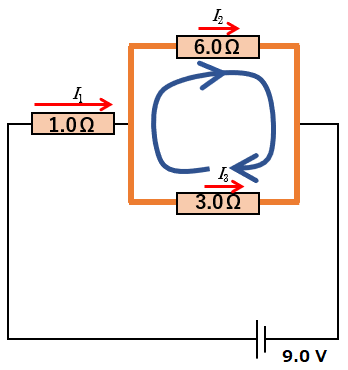
$0=-3.0\times I_3+6.0\times I_2\:\:\cdots (3)$

となります。
ここで、 $I_3$ は電流の過程の方向と、青の回転の向きが逆向きであるため、$-3.0\times I_3$　と $-$ が付くことに注意します。

すべての組み合わせについて式を考えましたが、キルヒホッフの第1法則の式　$I_1=I_2+I_3$　があるため、第2法則の式は $(1),\:(2),\:(3)$ のうち、2 つあればOKです。

というか、式 $(1),\:(2),\:(3)$ だけでは解けません。

ここでは、$I_1=I_2+I_3$　と、式 $(1),\:(2)$　を使って解いてみます。
　　他の組み合わせでもOKです。

$I_1=I_2+I_3$　より、 $I_3=I_1-I_2$

よって、

$9.0=1.0\times I_1+3.0\times I_3=1.0\times I_1+3.0\times (I_1-I_2)\:\:\cdots (1′)$

$9.0=1.0\times I_1+6.0\times I_2\:\:\cdots (2)$

より、$I_1=3.0 \:A$、$I_2=1.0\:A$、$I_3=2.0\:A$　となります。

ここでもし、負の値で得られたなら、

その電流の向きは仮定と逆向きであることを示しています。

この場合はすべて正の値を得ましたので、すべて仮定と同じ向きです。