単振動のエネルギーを使った解き方に2つの種類あるのをご存じですか。
この2つは明確に解き方に違いがあるので、混同すると大変なことになります。
今回は単振動でのエネルギー保存を使った解法についてわかりやすく、かつ詳しく解説します。
そして単振動エネルギーの使い方をマスターしたら、計算量が劇的に減り、かつシンプルに考えることができるようになるのです。
これはやらないと損! この記事を読んでぜひマスターしてください。
単振動のエネルギー解法2種
単振動をエネルギー保存則で解くとき、その方法は大きく分けて2種類あります。

単振動を考えるときのエネルギーには2種類あるんです。
- 重力の位置エネルギーを考える、
力学的エネルギー保存を使う方法 - 振動中心を考えて、
単振動エネルギー保存を考える方法
です。

それってどちらも一緒のことなのではないですか?

いいえ、この二つは違うんです。
そして、この違いを知るとややこしい単振動問題が
簡単に解けたりするんですよ。
これは絶対にマスターしておくべきです。
でも、なぜ2種類のエネルギーがあるのか?その違いは?・・・という問いに答えることができますか?
そして、さらなる難問にも立ち向かえます。
ぜひ、ここできっちりと理解して高得点を狙いましょう。
動画による解説
力学的エネルギー保存則を使う方法
バネの弾性エネルギーについてのおさらいです。バネのエネルギー $E_k$ はそのバネの自然長からの伸び(縮み)$x$ に関係しています。
つまり、バネ定数を $k$ として$E_k=\dfrac{1}{2}kx^2$と示されます。
では垂直につるされたバネを例にとって力学的エネルギーを考えていきましょう。
図のように自然長から $l_0 + x$ だけ伸びている位置で物体が速さ $v$ で運動しています。
つり合い位置は自然長から $l_0$ だけ伸びた位置です。
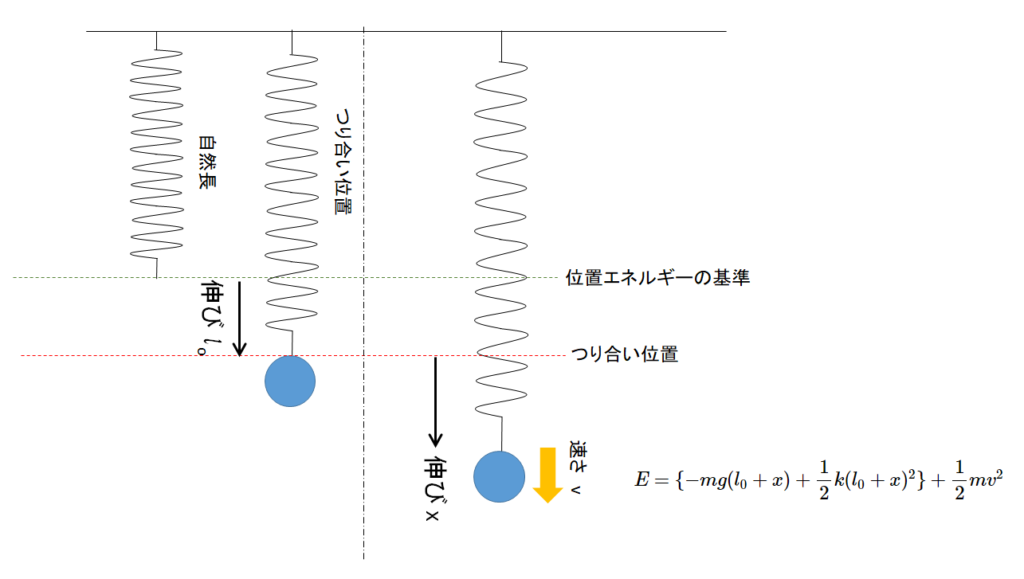
このとき、単振動する物体のもつ力学的エネルギー $E$ は
力学的エネルギー=(重力の位置エネルギー+弾性力の位置エネルギー)+運動エネルギー
ですから、重力の位置エネルギーの基準をバネの自然長のところにとってやると、
$\small E=\{-mg(l_0+x) + \dfrac{1}{2}k(l_0+x)^2\} + \dfrac{1}{2}mv^2 \normalsize$
と書けます。基本的には、このエネルギーが保存されるとして解けばいいですね。
では、気になる単振動のエネルギーの方法とはどのようなものでしょうか。
単振動エネルギー保存則を使う方法
そして、このことが計算を劇的に簡単にしてくれるんです。
そして O が単振動の振動中心になります。

単振動ではつり合い位置が振動中心になります!
なぜならば、運動していてもつり合い位置では瞬間的に合力 0 加速度 0 になるからです。

つまり、振動中心を考えてそこからの変位で単振動位置エネルギーを考えるのです。

めっちゃシンプルですね!
また、単振動に対する考え方も非常にシンプルになるので間違いも少なくなるはずです。

振動中心を考えて、そこからの距離 $x$ による
単振動位置エネルギーと運動エネルギー の和
$\dfrac{1}{2}kx^2 + \dfrac{1}{2}mv^2$
を考えることで重力の位置エネルギーが不要になるんだ。

でもなぜ重力の位置エネルギーを考えなくていいの?
次章ではなぜ重力の位置エネルギーを考える必要がないのかを検証します。
なぜ、重力による位置エネルギーを考えなくてもよいのか
その単振動エネルギーを使う解法はもう知っているよ!・・・という人もみえるでしょうが、再度お尋ねします。
なぜ重力の位置エネルギーを入れなくてもいいのでしょうか? 実際このなぜか、という説明が抜けている参考書がほとんどです。
ここではそのなぜを考えていきましょう。
仕事と力の関係
仕事 $W$ は、力を $F$、移動距離を $x$ とすると次式で示されます。
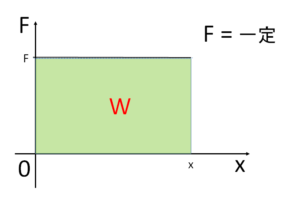
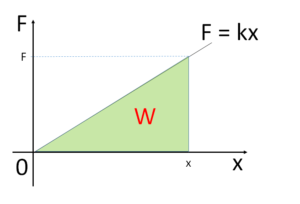
つまり、

力が$F=kx$ で示される場合のエネルギーは
$E=\dfrac{1}{2}kx^2$
なんだ!
振動中心からの合力

$F=mg-k(x+l_0)=-kx$

結局図を横にして眺めれば、次の図と同じことになります。
ただし振動中心は鉛直につるした場合のつり合い位置です。
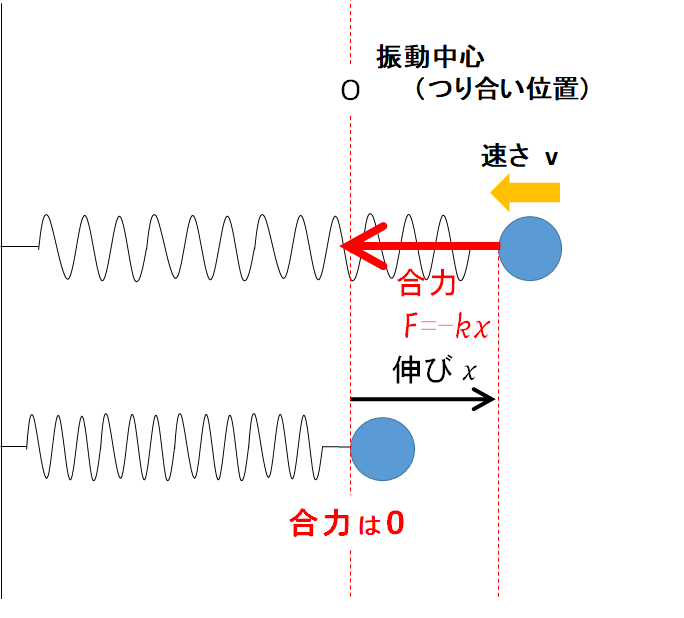
$\small E_S=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2 =\:一定\normalsize$
計算してみた
$\small ~~~=-kl_0(l_0+x) + \dfrac{1}{2}k\{l_0\!^2+2l_0x+x^2\} + \dfrac{1}{2}mv^2 \normalsize$
$\small ~~~=-\dfrac{1}{2}kl_0\!^2+\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2 =\:一定\normalsize$
となります。

なるほど!
わかりました!
問題を解くときはどちらを使うべきか
まとめ
- 力学的エネルギーを考える方法
力学的エネルギー=(重力の位置エネルギー+弾性力の位置エネルギー)+ 運動エネルギー
$\small E=\dfrac{1}{2}kx^2 + mgh + \dfrac{1}{2}mv^2 =\:一定\normalsize$- 振動中心を考えてそこからの変位 $x$ から単振動位置エネルギーを考える方法
単振動エネルギー= 単振動の位置エネエルギー+ 運動エネルギー
$\small E_S=\dfrac{1}{2}kx^2 + \dfrac{1}{2}mv^2 =\:一定\normalsize$
重力の位置エネルギーを使うことを要求されていなければ、単振動のエネルギーを使うのが断然おすすめです。
注意点として、テクニック的に使うのではなく、なぜかをよく理解して使ってください。
それが難問に立ち向かうための力となります。
最後に、難関大学をこれから目指す方で、基本をすでに終えているのであれば次の問題集がおすすめできます。
ホネのある問題が多いですが、とことん考える姿勢を養ってほしいと思います。
|
|
|
|









































コメント
音波とか電気信号の単振動でない振動のエネルギーのスペクトラム(デジタル的にサンプリングして離散スペクトラムで眺めるとき)も各振動数について振幅の二乗(スペクトラムなので複素数の大きさ[SQRT(a^2-(ib)^2)]の二乗[(a+ib)(a-ib)]かな?)に比例する式になるはずですが,仕事量を計算する積分で求める方法を使うのでしたっけ?