- コンデンサーと耐電圧
コンデンサーの耐電圧というのは、文字どおりコンデンサーが耐えられる電圧のことです。
コンデンサーに耐電圧以上の電圧がかかると、コンデンサーの絶縁が破れて極板間に電流が流れ、極板に貯められていた電荷が失われます。
コンデンサーというのは、蓄電器というくらいですから、電気を貯めてなんぼ・・・という機器です。つまり、絶縁が破れれば、コンデンサーとしての機能を失うのです。
なので、コンデンサーは必ず耐電圧以下で運用しなければなりません。コンデンサーにかけられる最大の電圧を求める場合、並列接続の場合は簡単なのですが、直列接続の場合はやや注意が必要です。以下、詳しく説明していますので参考にしてください。
動画
- コンデンサーの並列接続と耐電圧
コンデンサーと耐電圧
コンデンサーの耐電圧というのは、文字どおりコンデンサーが耐えられる電圧のことです。
コンデンサーに耐電圧以上の電圧がかかると、コンデンサーの絶縁が破れて極板間に電流が流れ、極板に貯められていた電荷が失われます。

コンデンサーというのは、蓄電器というくらいですから、電気を貯めてなんぼ・・・という機器です。つまり、絶縁が破れれば、コンデンサーとしての機能を失うのです。
なので、コンデンサーは必ず耐電圧以下で運用しなければなりません。
コンデンサーにかけられる最大の電圧を求める場合、並列接続の場合は簡単なのですが、直列接続の場合はやや注意が必要です。以下、詳しく説明していますので参考にしてください。
動画

なので、コンデンサーは必ず耐電圧以下で運用しなければなりません。
コンデンサーの並列接続と耐電圧
コンデンサーを並列につなぎます。
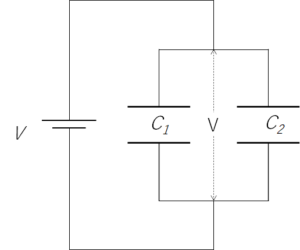
この場合、並列接続されたコンデンサーはどちらにも同じ電圧がかかります。
したがって、全体としての耐電圧は、それぞれのコンデンサーの耐電圧の低いほうになります。
例題
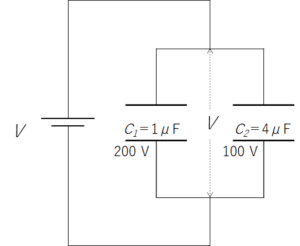
電気容量が 1 μF のコンデンサー $C_1$ と 4 μF の $C_2$ の耐電圧がそれぞれ 200 V 、100 V とする。
これのコンデンサーを並列に接続し、電源をつなぐ。電源電圧を次第に上げていくとき、これら並列接続されたコンデンサーにかけられる最大電圧を求めよ。また、そのときの、コンデンサーにたまる電気量を求めよ。
答え
コンデンサー $C_1$ と $C_2$ は並列接続であるため、それぞれのコンデンサーには同じ電圧がかかります。
したがって、並列接続されたコンデンサー全体としての耐電圧は 200 V 、100 V の低いほうになります。
したがって、答えは 100 V
並列接続なので、合成容量 $C$ は $ C = C_1 + C_2 = 1 + 4 = 5\:\mathrm{[μF]}$
たまる電気量 $Q = CV = 5\: \mathrm{[μF]} \times 100\: \mathrm{ [V]} =500\: \mathrm{ [μC]}$
コンデンサーの直列接続と耐電圧
コンデンサーを直列接続する場合は、並列接続の場合とは違い、ちょっと注意が必要です。
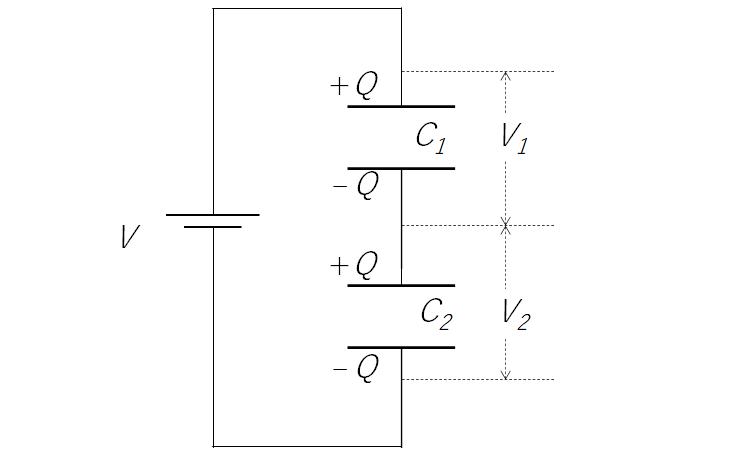
コンデンサー $C_1$ と $C_2$ を直列接続した場合を考えます。
それぞれのコンデンサーにかかる電圧を $V_1$ 、$V_2$ とすると、電源の電圧 $V$ は、 $V = V_1 + V_2$ となります。
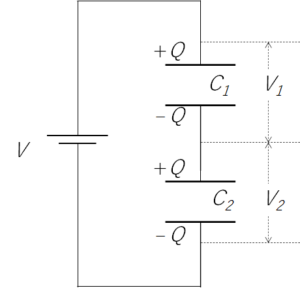
最初にコンデンサーに電荷がなければ、各コンデンサーにたまる電気量は同じです。
これを $Q$ とします。
そうすると、 $Q = CV$ より
$V_1:V_2 =\dfrac{Q}{C_1} : \dfrac{Q}{C_2}$
$~~~~~~~=C_2 : C_1$
電源電圧 $V$ のとき、 $V = V_1 + V_2$ であるから、
$V_1=\dfrac{C_2}{C_1+C_2}\times V$
$V_2=\dfrac{C_1}{C_1+C_2}\times V$
コンデンサー $C_1$ の耐電圧を $V_{max1}$ コンデンサー $C_2$ の耐電圧を $V_{max2}$ とした場合。
$V_1 \leqq V_{max1}$ かつ $V_2 \leqq V_{max2}$ である必要があります。
これにより、電源電圧の最大値を求めることができます。
以上に注意して次の問題をやってみましょう。
例題
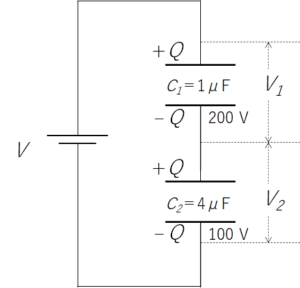 電気容量が 1 μF のコンデンサー $C_1$ と 4 μF の $C_2$ の耐電圧がそれぞれ 200 V 、100 V とする。
電気容量が 1 μF のコンデンサー $C_1$ と 4 μF の $C_2$ の耐電圧がそれぞれ 200 V 、100 V とする。
これのコンデンサーを直列に接続し、電源をつなぐ。電源電圧を次第に上げていくとき、かけられる最大の電源電圧 $V$ を求めよ。
またそのとき、コンデンサー $C_1$ とコンデンサー $C_2$ にたまる電気量をそれぞれ求めよ。
答え
電気容量が 1 μF のコンデンサー $C_1$ と 4 μF の $C_2$ にかかる電圧をそれぞれ $V_1$ 、$V_2$ とします。
直列接続であるから、コンデンサー全体にかかる電圧(ここでは電源の電圧) $V$ は、 $V = V_1 + V_2$ となります。

ここで、最大電圧 $V$ を
$V = V_1 + V_2=200+100=300\:\mathrm{[V]}$
としてはいけません。
最初にコンデンサーに電荷がなければ、各コンデンサーにたまる電気量 $Q$ は同じです。
$Q = CV$ より、
$V_1:V_2 =\dfrac{Q}{C_1} : \dfrac{Q}{C_2}$
$~~~~~~~=C_2 : C_1$
$~~~~~~~=4 : 1 $
電源電圧 $V$ のとき、 $V = V_1 + V_2$ であるから、
$V_1=\dfrac{4}{4+1}\times V=\dfrac{4}{5}\times V$
$V_2=\dfrac{1}{4+1}\times V=\dfrac{1}{5}\times V$
コンデンサー $C_1$ の耐電圧が 200 V コンデンサー $C_2$ の耐電圧が 100 V ですから、
$V_1 \leqq 200 $ かつ $V_2 \leqq 100 $ である必要があります。
つまり、
$V_1=\dfrac{4}{5}\times V \leqq 200 \:\: \cdots \cdots (1)$
$V_2=\dfrac{1}{5}\times V \leqq 100 \:\: \cdots \cdots (2)$
のどちらも満たす必要があります。
(1) より、$V \leqq 250\: \mathrm{[V]}$ (2) より、$V \leqq 500\: \mathrm{[V]}$ これより、電源電圧は最大 250 V であることがわかります。

なぜって?
もし500 Vかけてしまった場合、$C_2 $ にかかる電圧は 100 V で条件を満たしますが、$C_1$ にかかる電圧は 400 V となり耐電圧の 200 V を超えてしまうからですね。
コンデンサーにたまる電気量 $Q$ ですが、最大の電源電圧は 250 V ですから、
$V_1=\dfrac{4}{5}\times 250 = 200 \: \mathrm{[V]}$
$V_2=\dfrac{1}{5}\times 250 = 50 \: \mathrm{[V]}$
となります。したがって、
$Q=CV=C_1V=C_2V=1 \: [\mathrm{\mu F}] \times 200 \: [\mathrm{V}]=4\:[\mathrm{\mu F}] \times 50 \: [\mathrm{V}]=200 \:[\mathrm{\mu C}]$
です。
エッセンス動画解説
以下で耐電圧に関するエッセンス動画解説を行っています。





































コメント