変位
変位とは、物体がどの向きにどれだけ移動したかを示す量です。
一直線上
一直線上の運動について図にしてみましょう。図の右を正方向とします。
図のような運動をする物体があったとすると、点 $A$ から $B$ の変位は図の位置となります。

この場合、道中いろいろな動きをしても、点 $A$ から $B$ への変位というのは図の $x$ になります。
つまり、次の場合も変位は $x$ としてあらわされます。

あなたが通学をして自宅に戻ったら、自宅を基準とした場合、その変位は $0$ です。

そして、直線運動では変位 $x$ は、変位の向きを正負の記号で示すことができます。

上の図で最終的に赤い矢印で示される変位は、図の右を正とした場合、マイナスで表されます。
ある点を基準とした場合の変位は、次の図のようにベクトルで示されるものです。

これに対して、「道のり」は総合的に移動した距離です。したがって自宅と学校を往復すれば、変位は $0$ ですが、道のりは片道の長さの2倍になります。
位置ベクトル
さて、直線上だけではなく、平面にまで変位を拡張して考えましょう。
図の緑の矢印が、平面での位置を示しています。
ヘリコプターにゴムひもが付いているイメージです。
このとき、原点 $O$ から伸びている緑の矢印を、ヘリコプターの位置ベクトル $\vec{r}$ と名付けます。
この位置ベクトル $\vec{r}$ は $x$ 成分と $y$ 成分を用いて $(x,\:y)$ のように示すことができます。
変位
平面
ヘリコプターが飛んで、$x-y$ 平面内で、点 $P$ から $Q$ まで移動したとします。
このとき、点 $P$ から点 $Q$ まで引いた矢印を考えて、変位と呼ぶことにします。
図の $x-y$ 座標で、点 $P$ と点 $Q$ の位置ベクトルを考えて、それぞれ $\vec{r}_P$ 、$\vec{r}_Q$ とした場合、変位ベクトル $\Delta \vec{r}$ は
$\Delta \vec{r}=\vec{r}_Q-\vec{r}_P$
として示されます。
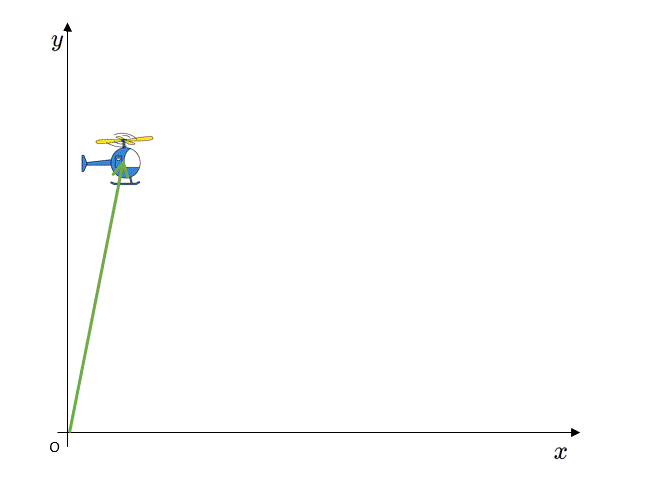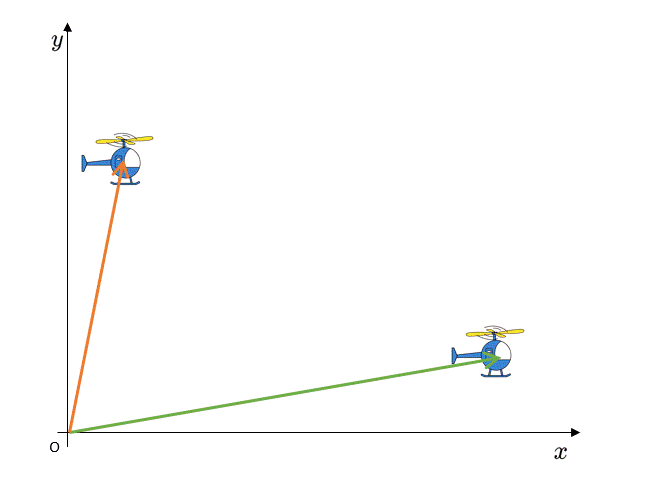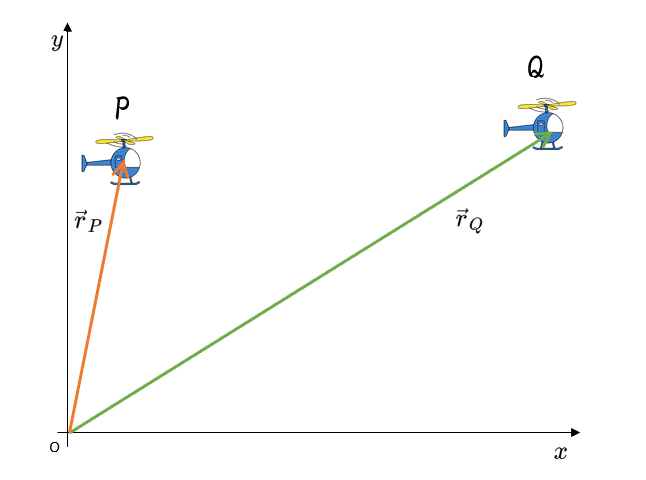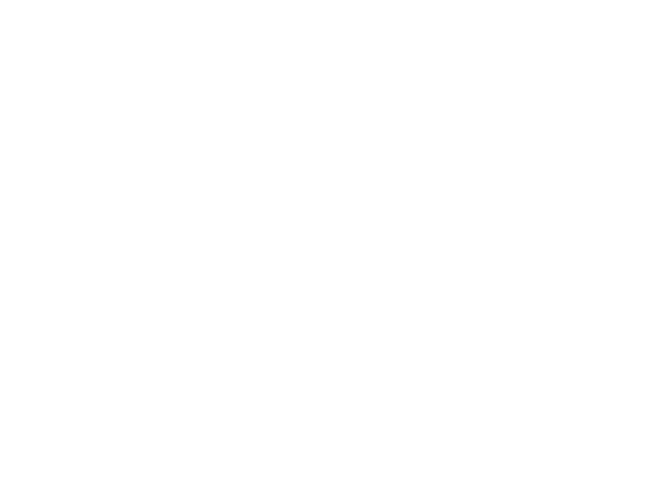
この場合の変位ベクトルは最初と最後、つまり $P$ と $Q$ の位置ベクトルだけで決まります。
ゆえに途中、ヘリコプターがどのような動きをしても変位は同じです。
空間
当然ですが、これを3次元空間に拡張して考えても同じことです。
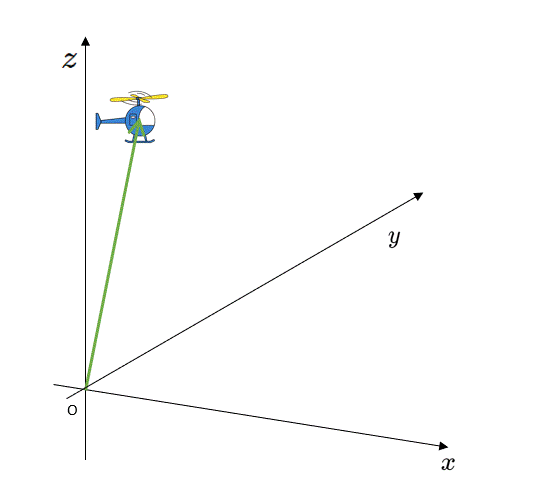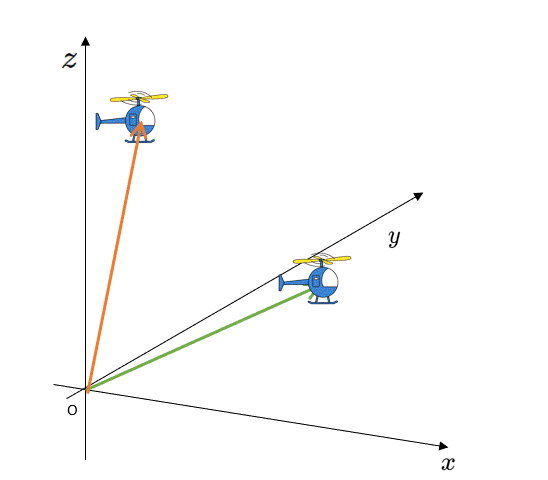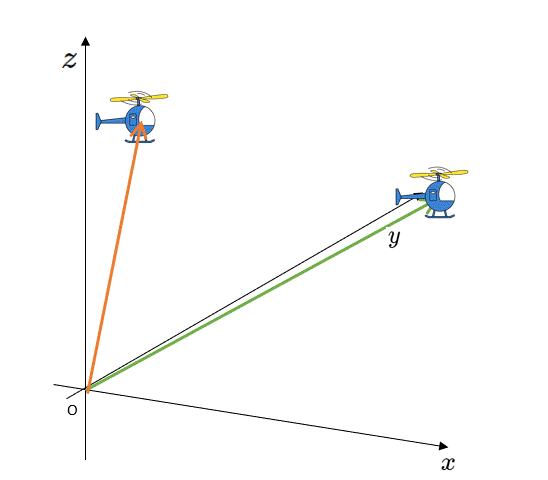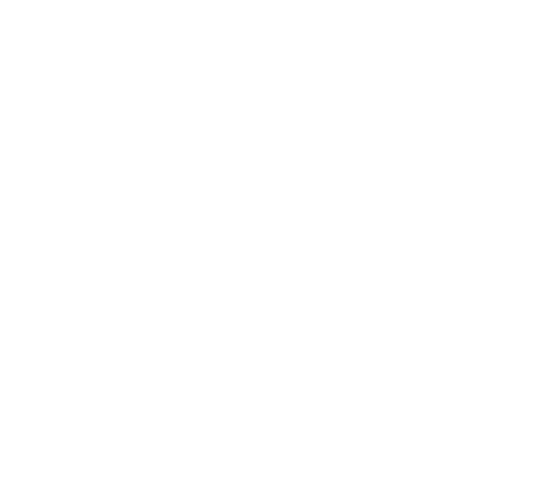
ヘリコプターが空間をどのように飛んでも、最初の位置 $P$ と最後の位置 $Q$ による変位ベクトルが考えられ、それは、
$\Delta \vec{r}=\vec{r}_Q-\vec{r}_P$
で示されます。
速度や速さについては次の記事をご覧ください。





































コメント