物理のエッセンス 力学33番 転倒問題
転倒問題です。
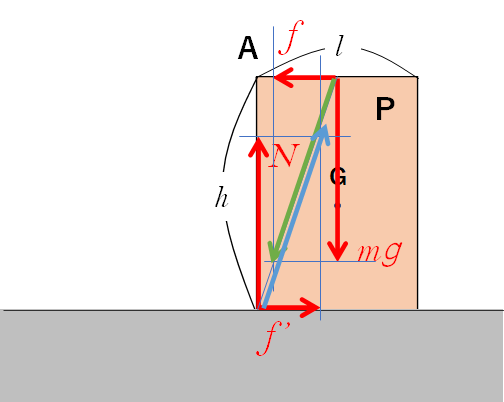
直方体の物体の上端を力 $f$ で水平に引きます。
床と物体の間には摩擦があり、力 $f$ を増していくと物体は転倒しようとしました。
そのときの値 $f_1$ と物体と床の静止摩擦係数 $\mu$ の範囲を求めます。
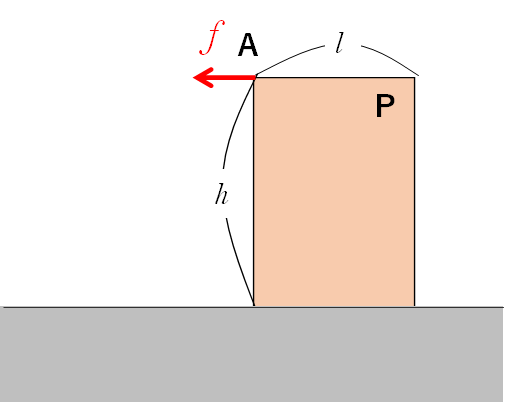
解説
注意：わかりづらい部分を少し書き直しました。
図が平面的に描かれているため、うまくイメージができない人を見かけます。
以下の図でイメージを作ってください。
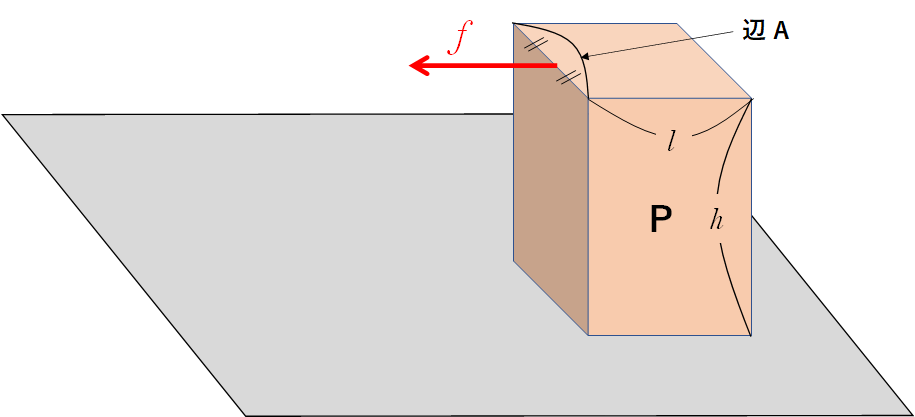
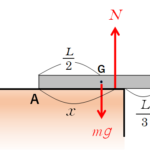
いわゆる転倒問題では、物体を引く力を変化させると垂直抗力のはたらく位置が変化します。
そして、転倒するときは垂直抗力が物体の端にまで来ている必要があります。
なぜなら、物体の右端が浮き始めるときに接触しているのは物体の左端のみだからです。
ちょっと説明すると
- 物体を水平に引く力がないとき・・・垂直抗力は重心の真下の位置にある。
- 物体を少し引くと・・・垂直抗力が図の左に移動する。
なぜでしょうか？
物体が静止している場合、物体の重力 $mg$ と水平に引く力 $f$ の合力は、物体にはたらく垂直抗力 $N$ と摩擦力 $f^{\prime}$ の合力とつり合います。
したがって、つりあうためにはそれらの合力は1直線上反対に位置します（図）。
そのため、力 $f$ を大きくしていくと垂直抗力と摩擦力のはたらく位置はずれるのです。
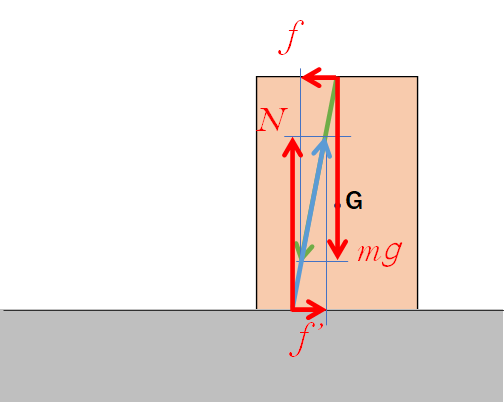
次のアニメにあるように、引く力を大きくしていくにつれて、垂直抗力 $N$ と摩擦力の作用点はだんだんと図の左方向にずれていきます。
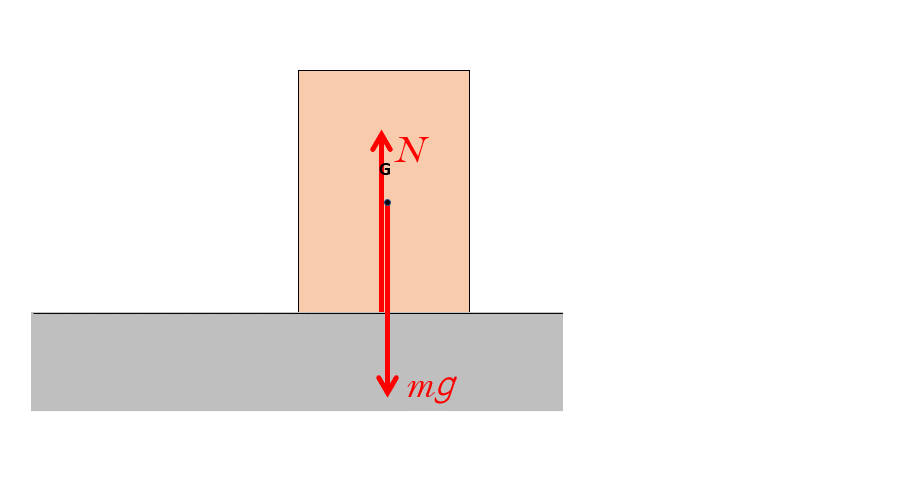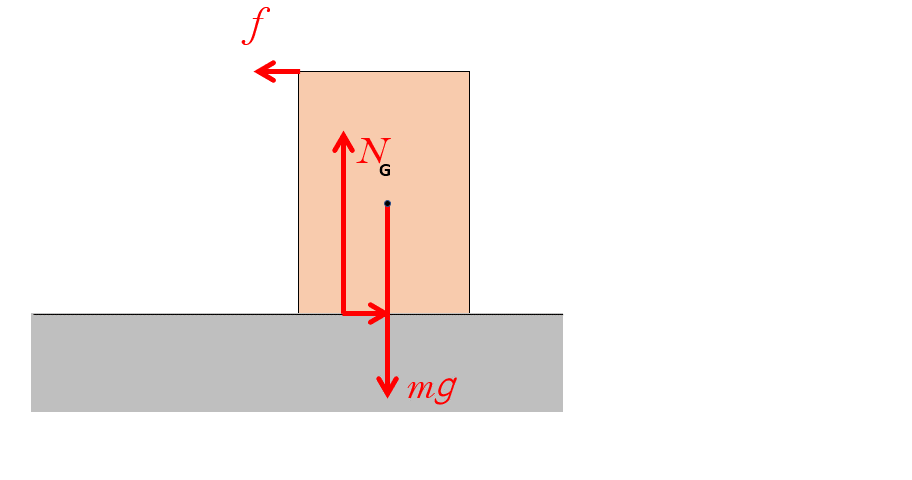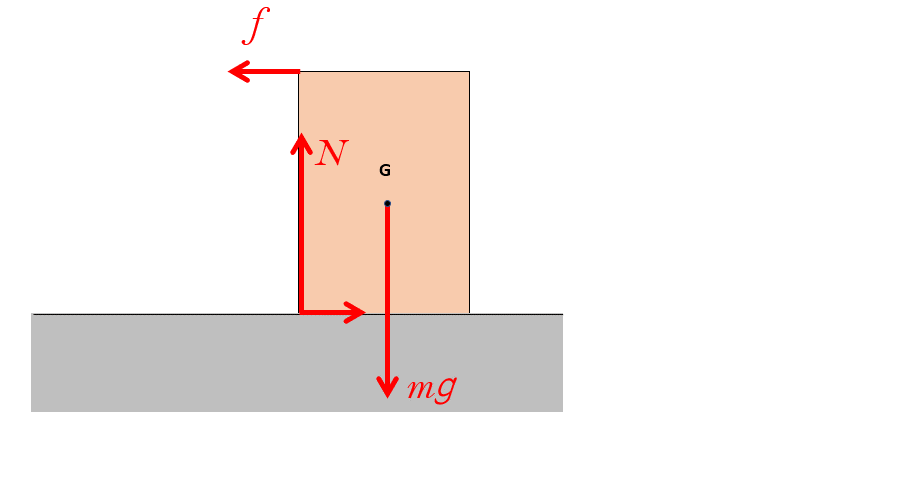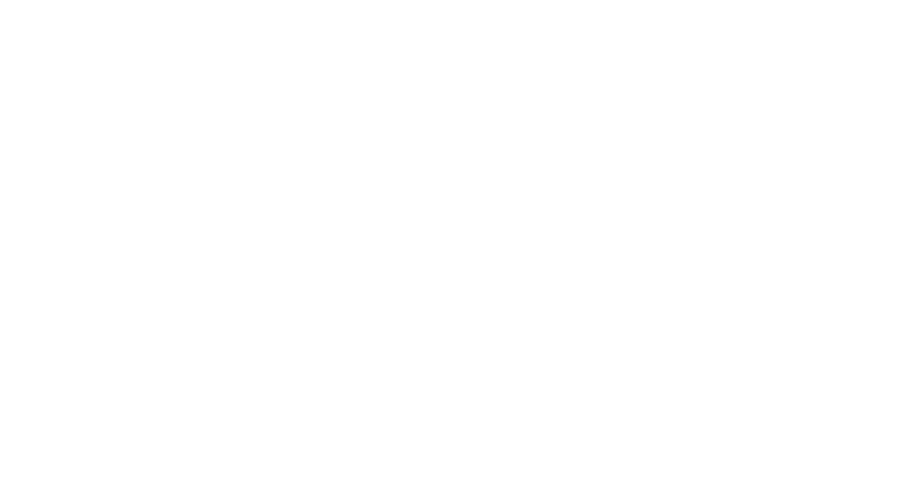
もし、物体が滑ることがなければ、垂直抗力は物体の端まで移動してそこで止まります。
なぜかというと、垂直抗力は物体と床が接触していないところには存在できないからです。
そしてそれ以降は物体の左端を中心として回転し、転倒していくことになります。
次の動画でも解説しています。
このことさえ理解できれば、後は普通の剛体の問題の解き方でOKです。
剛体の問題を解くには以下のようにします。
基本的に剛体の問題の解き方は決まっています。
それは
- 図を描いて、注目物体にはたらく力をすべてかき入れる。← 最重要
- 力のつりあいの式をたてる
- ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
- 以上の式を連立する
です。
多少の違いはあります（手順2・3などの一部が不要なこともあります）が、基本的にはこのようにすればほとんどの問題の糸口はつかめるはずです。
図を描いて、注目物体にはたらく力をすべてかき入れる。← 最重要
注目物体に力をかき入れます。
これが正確にできないと正解にはたどりつけませんので、慎重に。
いままさに物体の右端が浮き始める・・・という瞬間を考えます。
このとき物体は静止していると考えます。
物体と床の摩擦力を $f^{\prime}$ 、垂直抗力を $N$ とします。
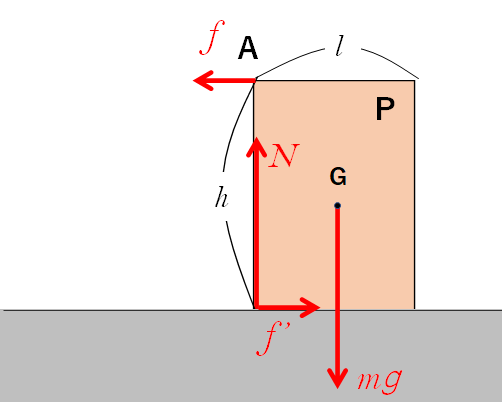
剛体においては力は物体上であれば一直線上を移動しても効果は同じです。
したがって、次のようにもかけますね。
緑で示された合力と青で示された合力がつり合っています。
力のつりあいの式をたてる
鉛直方向
鉛直方向の力のつりあいを考えます。
$mg=N \:\:\cdots\cdots \:(1) $
水平方向
$ f_1 = f^{\prime} \:\:\cdots\cdots \:(2) $
ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
図の物体の端っこの O のまわりのモーメントを考えます。
$f_1h = mg\dfrac{l}{2} \:\:\cdots\cdots \:(3) $
以上の式を連立する
式(3) から、
$f_1=\dfrac{mgl}{2h}$
ここで、物体が滑らないためには傾くときの摩擦力 $f^{\prime}$ が最大摩擦力 $\mu N$ 以下であればよいということになります。
したがって $N=\mu mg$ として、
$f^{\prime}=f_1 \leqq \mu N=\mu mg$
$\dfrac{mgl}{2h}\leqq \mu mg $
整理して
$\mu \geqq \dfrac{l}{2h}$
コメント