物理のエッセンス　力学37番

物理のエッセンス　力学37番

半径 $R$ の円盤から、半径 $r$ の円盤をくりぬいた場合の重心位置を求めます。

解説

図のように座標を考えます。

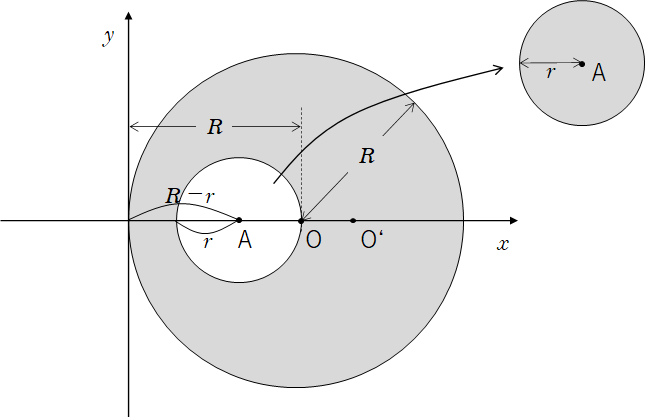
ここで、

• くりぬく前の円盤の重心を O 
• くりぬいた円盤の重心を A 
• くりぬいた後の穴の空いた円盤の重心を O’

とします。これらは上図のように $x-y$ 軸をとれば、$x$ 上にのります。

ここでは、

• 円盤をくりぬいた後の穴のあいた物体の質量を $M$
• くりぬいた円盤の質量を $m$

としましょう（下図）。

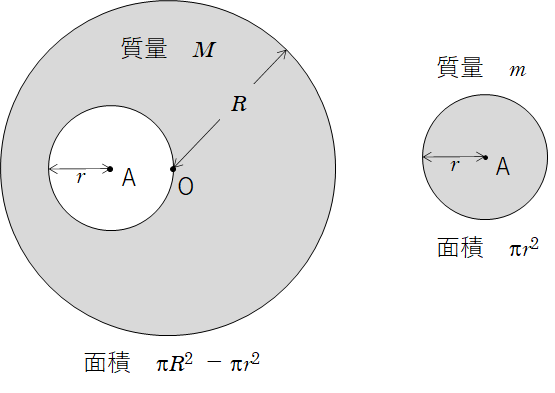
さて、質量 $m$ の小さい円盤と、質量 $M$ の穴の空いた大きな円盤の2つをもとどおりはめると、くりぬいていない円盤になります。

したがって、その重心は O 点にくるはず・・・・というのが戦略です。

今回は重心公式を用いて考えてみました。

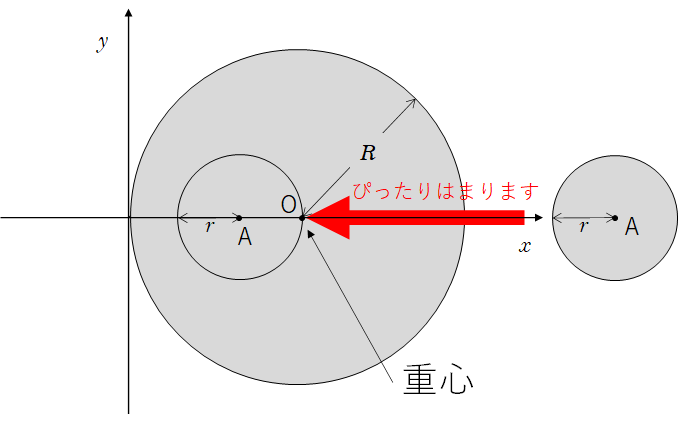
計算をするうえで、重心公式を使うイメージとしては次の図と同じことです。

つまり、

• 質量 $m$ の物体が A（座標 $R-r$）
• 質量 $M$ の物体が O’（座標 $x$）
• それらの重心が O（座標 $R$）

にくる・・・というわけです。

そこで、それぞれの質量を求めるのですが、円盤が均一な材料でできているとすると、質量比は面積比に等しくなります。

なぜなら、円盤の材質の密度 、円盤の厚み、面積には次の関係があるからです。

 

質量 = 密度 × 体積 = 密度 × (厚み × 面積)

 

円盤が大きくても小さくても、密度と厚みは同じですから、質量比は面積比に等しくなります。

では、質量比を面積比によって求めます。くりぬいた物体の面積は、 $(\pi R^2 -\: \pi r^2)$　です。
よって、

$M:m=(\pi R^2 – \:\pi r^2) : \pi r^2 = (R^2 -\: r^2) : r^2\:\:\cdots\cdots\:(1) $

また、それぞれの $x$ 座標は

A ・・・ $R-r$　　　O ・・・ $R$　　　O’ ・・・ $x$

であることから、重心公式を活用して、

重心公式は

 

$x_G=\dfrac{m_1x_1+m_2x_2+m_3x_3+\cdots}{m_1+m_2+m_3+\cdots}$

 

力学 剛体 重心・合力・転倒条件　やさしく解説

剛体は制しやすい分野です。 この記事で理解を深めることができれば得点源間違いなしです！

kokolainen.com

よって、

• 重心 $x_G=R$
• $x_1=(R-r)$
• $x_2=x$
• $m_1=m$
• $m_2=M$

として、

$x_G=\dfrac{m_1x_1+m_2x_2}{m_1+m_2}$

$R=\dfrac{m(R-r)+Mx}{m+M}$

これから

$x=R + \dfrac{m}{M}r$

式(1)から　$\dfrac{m}{M}=\dfrac{r^2}{R^2-r^2}$　として代入します（どのように代入してもOKです）。

よって、

$x=R + \dfrac{r^3}{R^2-r^2}$

を得ます。

答えかたですが、この問題では

直線AO上で O より右に　$\dfrac{r^3}{R^2-r^2}$　の位置

とでもしておきましょう。

動画で解説