$v-t$ 図を積極的に活用しましょう。
きっとあなたを助けてくれる強力なツールとなります。
さらに有効な $v-t$ グラフの活用方法についてはこちらへ ⇒ v-tグラフ・反発問題テクニック
物理のエッセンス力学編3番
問題概要
初速度 $20 \: [\mathrm{m/s}]$ 加速度 $-4 \:[\mathrm{m/s^2}]$ で運動する物体がある。
スタートしてから速度が $-12\:[\mathrm{m/s}]$ になるまでにかかる時間 $t$ とその間の走行距離 $l$ をもとめる。
解説
時刻
$v-t$ 図を描いてみましょう。
それだけで多くのことがイメージでき、理解することができます。
加速度が $-4 \:[\mathrm{m/s^2}]$ であることから、$v-t$ 図の傾きは $-4$ です。
初速度が $20 \: [\mathrm{m/s}]$ だから $t$ 軸は $5$ を通ります。
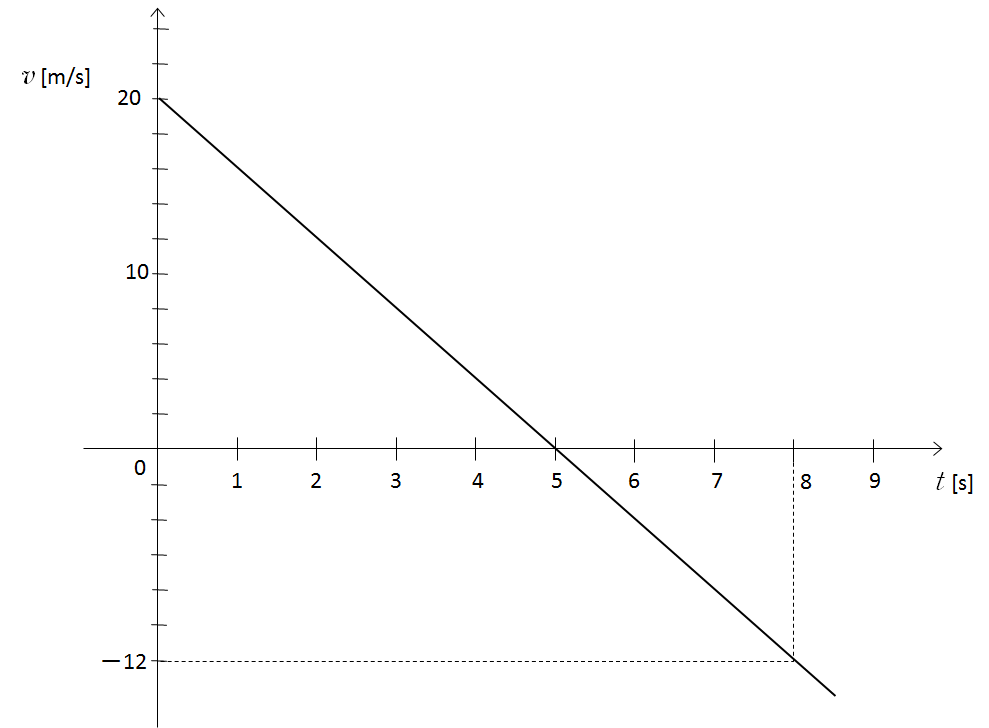
図の三角形は相似です。
相似比から $20:5=|-12|: T $ とすると、
$T=3$ となりますから、$-12\:[\mathrm{m/s}]$ になる時刻は $5+3=8\:[\mathrm{s}]$ です。

そんな計算をしなくても、グラフを見ればすぐにわかりますね。
走行距離
注意:走行距離と変位は違います。
ここでいう走行距離とは、文字通り走った全距離のことです。
したがって、図の水色の部分の総面積を求めればよいことになります。
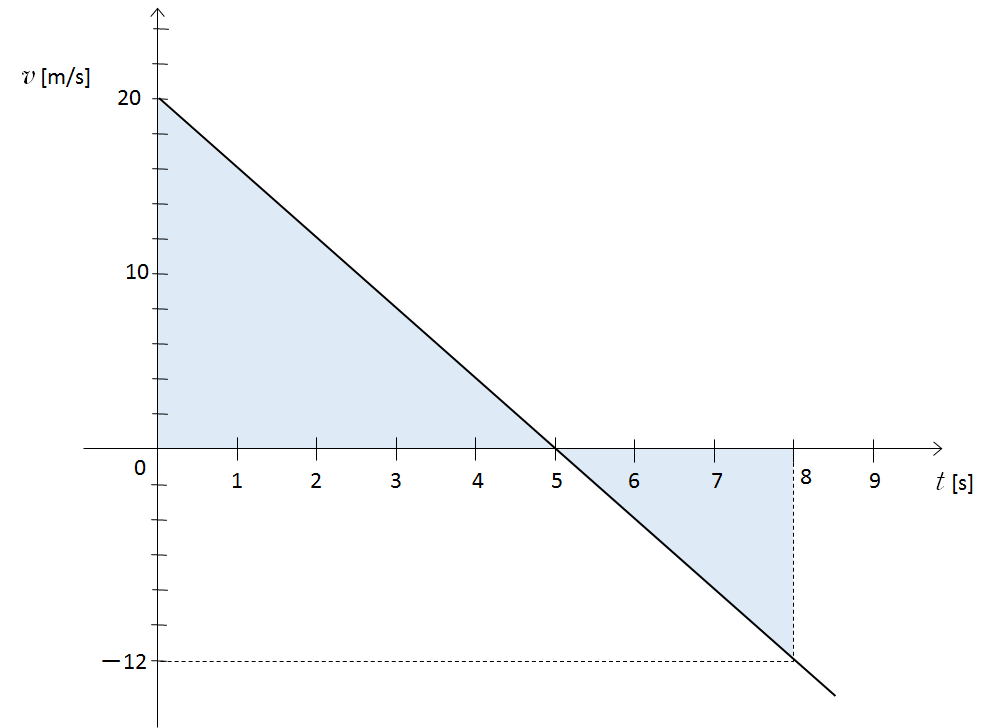

変位の場合は $t$ 軸より上の面積を正、下の面積を負としてやります。
では面積を計算して $l$ を算出しましょう。
$l=5\times 20 \div 2 + 3 \times 12 \div 2 =50 + 18 =68 \:[\mathrm{m}]$
答え $68 \:[\mathrm{m}]$

さらに有効な $v-t$ グラフの活用方法
$v-t$ グラフと $t$ 軸の囲む面積が走行距離・変位を示す
こと等については 以下の解説を参照してください。




































コメント