落体の運動の考え方
次の問いを考えてみてください。
次の運動の加速度の大きさ $a_1\:,\:a_2\:,\:a_3$ を大きい順に並べてください。
- ボールを自由落下させる 加速度の大きさ $a_1$
- 鉛直上方にボールを投げる 加速度の大きさ $a_2$
- 鉛直下方にボールを投げおろす 加速度の大きさ $a_3$
選択肢
-
- $a_3>a_1>a_2$
- $a_2>a_1>a_3$
- $a_1>a_3>a_2$
- $a_1=a_2=a_3$

答え
もちろん 4 の $a_1=a_2=a_3$ です。
あってましたか?
落体の運動の学習は、自由落下から始まって、鉛直投げ上げ・鉛直投げ下ろし・水平投射・斜方投射、と続きます。
初めて物理を学習している人の様子を見ると、これらを別々の運動と考えて、$v=gt$ 、$v=v_0-gt$ 、$v=v_0+gt$ $\cdots$ etc などと念仏のごとく唱える人を見ますが、ぶっちゃけ無駄です。
無駄ならまだいいのですが、逆効果になることもあります。
物理学とは、基本的な理解さえできればちょっとした複雑な運動など、その組み合わせで理解できるようになっていると考えてください。
落体の運動の場合も同様です。もっと言えば、加速度運動全般に対してもそう言えるのですが、ここでは落体にかぎってお話を進めていきましょう。
重力だけがはたらく運動
もっとも重要なこと
- $a_3>a_1>a_2$
- $a_2>a_1>a_3$
- $a_1>a_3>a_2$
- $a_1=a_2=a_3$

あってましたか?
先ほどの問題で、重力だけを受けて運動する場合の加速度はすべて同じとしました。
重力だけがはたらく運動の場合では加速度が特別です。
つまり、すべての場合において $g$ という加速度(重力加速度)だということです。
なぜでしょうか?
ニュートンの第2法則 $ma=F$ を学習した人は、次のように考えてみましょう。
地球上では物体は万有引力により地球から力を受けています。
物体の質量を $m$ とすると、力の大きさは、地表の範囲ではおおむね $mg$ です。
したがって、鉛直方向の運動方程式を立てると、$ma=F$ より $F=mg$ として、$ma=mg$ です。
つまり、$a=g$ で加速度はいつも同じ $g$ なのです。
他の場合、例えば、自動車などが加速運動する場合はその都度変わってきますね。
「そんなことは知っているよ」・・・などといわれるかもしれませんが、意外とわかっているようでも、うまく使えていないことが多いようです。
この特異な性質、「重力だけを受けて運動する場合の加速度の大きさは、すべて $g$ 」を使うと落体の公式など覚える必要はありません。
また、$v-t$ グラフなどで、この性質を利用すると簡単に問題が解けることも多々あるのです。
ではまず、式の導出からやってみましょう。
加速度を $a$、$t$ 秒後の速度を $v$、初速度を $v_0$ とすると、加速度は速度変化 $\Delta v$ を時間変化 $\Delta t$ で割ったものですから、
$$a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{t}$$
となります。
これは、一般的な加速度の意味・定義です。
したがって、これはよく理解しておいてください。

加速度とは、単位時間当たりの
速度の変化を示しているのですね。
この式を変形して、$v=v_0+at$ というおなじみの式が出ます。
そして、落体の場合の加速度はすべて $g$ です。
したがって、 $a$ を $g$ と書き換えて $v=v_0+gt$ と書くことができます。
次に、$x=v_0t+\dfrac{1}{2}at^2$ ですね。
これも同様に $a$ を $g$ と書き換えます。ついでに $x$ も $y$ と書き換えましょう。
$y=v_0t+\dfrac{1}{2}gt^2$
ついでに、$v^2-v^2_0=2gy$ 付け加えておきます。(これは上の2式から $t$ を消去すれば出ます)
まとめると、
| $v=v_0+at$ | $\rightarrow \:\:$ | $v=v_0+gt$ |
| $x=v_0t+\dfrac{1}{2}at^2$ | $\rightarrow \:\: $ | $y=v_0t+\dfrac{1}{2}gt^2$ |
| $v^2-v^2_0=2ax$ | $\rightarrow \:\: $ | $v^2-v^2_0=2gy$ |
つまり同じことですね。
これでおしまいです。

いや・・・他にもいっぱい式があるけど・・・

そうですが、基本的には同じ事です。
他の式は、その運動方向を考えることで導けます。
まず自由落下では、$v_0=0$ です。
次に鉛直投げ上げ。この時は鉛直上方を正にとっても、$g$ の方向は常に下向き(上昇中でも下向きです!)なので、$a=-g$ とするだけです。
そして鉛直投げ下ろし。この場合は鉛直下方を正にとれば、そのままの式でOKです。
まとめてみると、
| 自由落下 | 投げ上げ | 投げおろし | ||
| $v=v_0+at$ | $\rightarrow \:\:\:$ | $v=gt$ | $v=v_0-gt$ | $v=v_0+gt$ |
| $x=v_0t+\dfrac{1}{2}at^2$ | $\rightarrow \:\:\:$ | $y=\dfrac{1}{2}gt^2$ | $y=v_0t-\dfrac{1}{2}gt^2$ | $y=v_0t+\dfrac{1}{2}gt^2$ |
| $v^2-v^2_0=2ax$ | $\rightarrow \:\:\:$ | $v^2=2gy$ | $v^2-v^2_0=-2gy$ | $v^2-v^2_0=2gy$ |
以上は基本的に、初速度の方向を正にとっています。

大きな注意点ですが、正にとる方向は特に決まっていません。
上は一例に過ぎません。
どの方向に正をとろうがあなたの自由です。
(ただし、普通の場合は初速度の方向を正にとるといいと思います)
問題によっては、正にとる方向を指定されている場合もあります。
しかし、その場合も考え方は同じ事です。
水平投射・斜方投射
水平投射・斜方投射についてもシンプルな話です。
これらは鉛直方向と水平方向に分けて考えれば済む話です。
水平方向には等速運動
重力だけを受けて運動するする場合、斜めに投げても考え方は同じことです。
鉛直方向には重力が常にかかり、ニュートンの運動の第2法則に従って加速運動します。
水平方向には力がかかっていないため、慣性の法則により等速直線運動するのです。
初速度 $v_0$ で $\theta$ だけ斜めに投げ上げた場合を考えます。
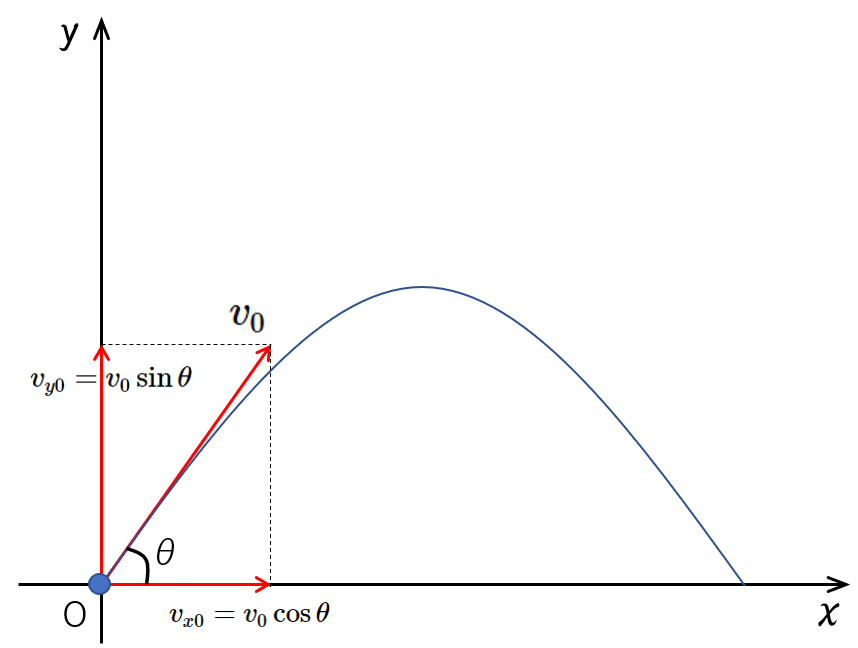
このときかなり多くの人が間違えるのですが、斜め方向の初速度($v_0$ ) が上の表で示した、どの式にも、そのままの形で代入されることはありません。初学者には、これをそのまま代入してしまう間違いが非常に多く見られます。
斜方投射の場合、初速度を鉛直方向と水平方向に分解して用いる必要があります。
つまり、鉛直方向の初速度は $v_{y0}=v_0\sin \theta$ 、水平方向の初速度は $v_{x0}=v_0\cos\theta$ とするだけです。
したがって、鉛直方向には初速度に注意して、加速度の式を用い、水平方向には $x=v_{x0}t$ の等速運動の式を使うだけです。
まとめると、図の斜方投射の場合、次のような式になります。
加速度は鉛直方向に $-g$ です。(鉛直上方を正)
| $y$ 軸方向 | ||
| $v=v_0+at$ | $\rightarrow \:\:\:$ | $v_y=v_0\sin \theta-gt$ |
| $x=v_0t+\dfrac{1}{2}at^2$ | $\rightarrow \:\:\:$ | $y=(v_0\sin \theta)t-\dfrac{1}{2}gt^2$ |
| $v^2-v^2_0=2ax$ | $\rightarrow \:\:\:$ | $v^2_y-(v_0\sin \theta)^2_0=-2gy$ |
$x$ 軸方向(水平方向)へは、等速直線運動しますから、 $x=v_{x0}t=(v_0\cos\theta) \times t$ です。
ちなみに正の方向を鉛直下方へとってもかまいません。
その場合は、$y$ 方向の初速度が $-v_0\sin \theta$ 、重力加速度は $g$ となります。






































コメント