定常波は振幅、波長、周期、波の速さが全く同じ波が一直線上・左右からぶつかる時に生じます。
しかし、波長、周期(波の速さ)が全く同じで、振幅だけが違う波が一直線上・左右からぶつかる場合、定常波にはならず、合成波は移動します。
定常波の波の式
定常波
定常波とは、一直線上・左右から全く同じ振幅、波長、振動数の波が同じ速さで伝わってきた結果、合成波が左右に移動せず、その場でのたうち回る(ちょっと例えが悪い・・・)ような波が観測される現象です。

まず最初に、定常波が生じる場合について考えてみましょう。
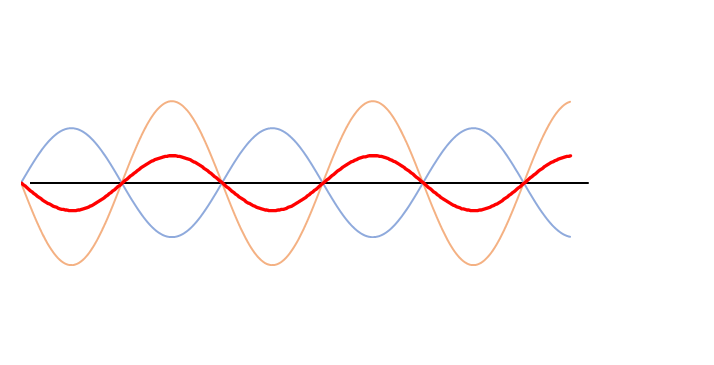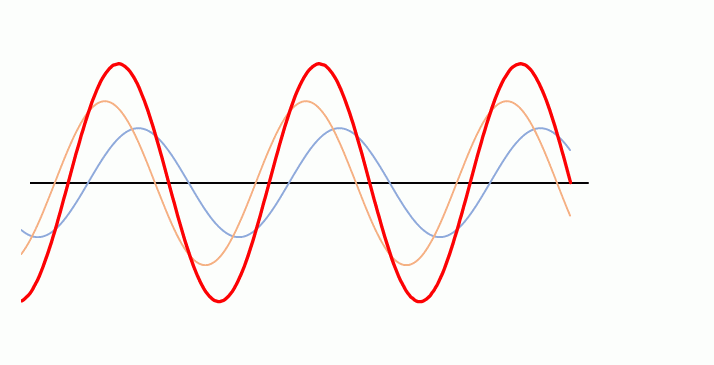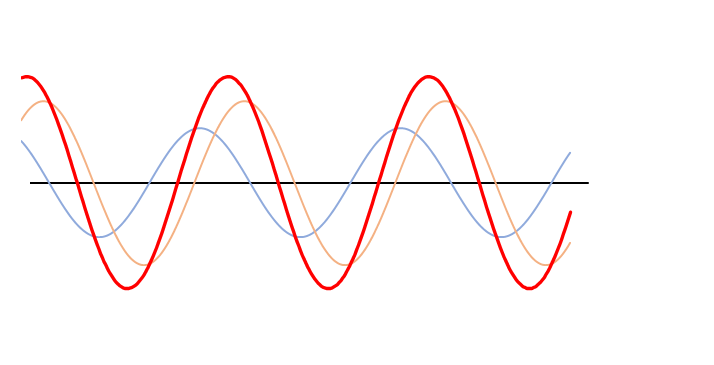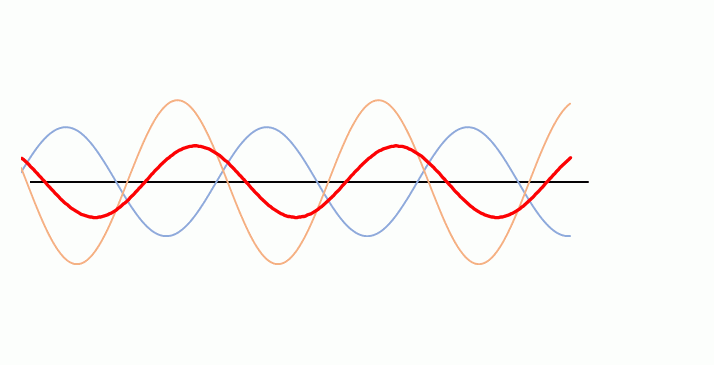
次の図では左右から、振幅、波長、振動数、波の速さ が全く同じである、青とオレンジの波が進んできています。
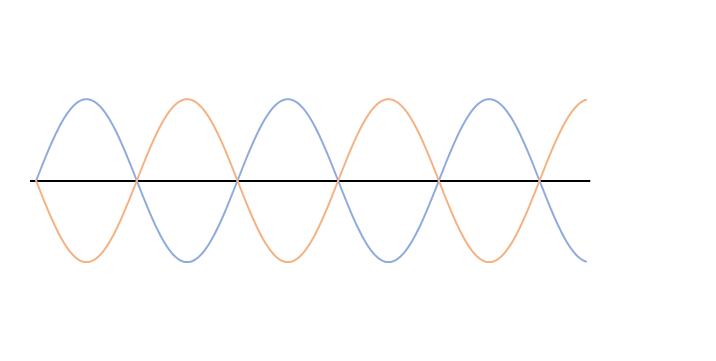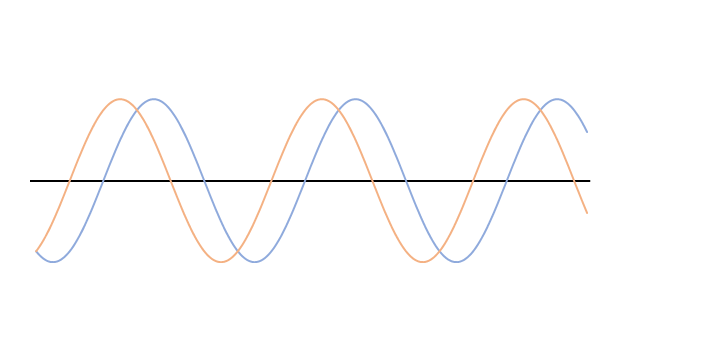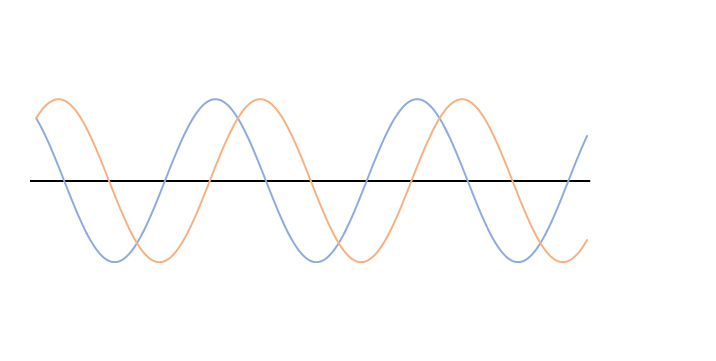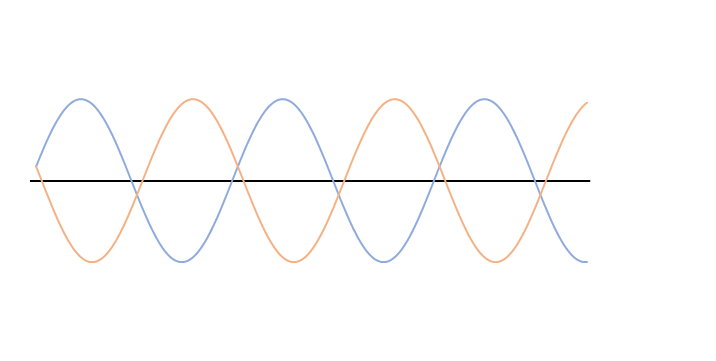
このとき、この青とオレンジの2つの波を合成します。
次の図の赤い波が合成波です。
この合成波(赤い波)は左右に移動せず、その場で振動しているように見えます。
定常波の振幅は元の波の振幅の2倍です。

この赤い波を定常波(定在波)と呼びます。
つまり、定常波ができるためには、左右からやってくる波はそれぞれ振幅、波長、振動数が全く同じ(したがって波の速さも同じ)である必要があります。

振幅も一緒である必要があるのでしょうか?

定常波の波の式
続いて、定常波を表す式を考えましょう。
基礎知識
原点での振動が $y_0=A\sin \omega t=A\sin 2\pi f t=A\sin \dfrac{2\pi}{T}t$ で示されるとき、
原点からの変位を $x$ とすると、波の一般式は以下で示されます。
$y=A\sin\omega(t-t’)=A\sin 2\pi f(t-t’)$
$~~=A\sin 2\pi f\left(t-\dfrac{x}{v}\right)=A\sin 2\pi \left(\dfrac{t}{T}-\dfrac{x}{\lambda}\right)$
$A$:振幅 $f$:振動数 $v$:波の速さ $T$:周期 $\lambda$:波長 $\omega$:角速度(角振動数)
$t’$ は、波の速さが $v$ のとき、原点から位置 $x$ まで波が伝わるのに必要な時間。
ゆえに、 $t’=\dfrac{x}{v}$一般的な波の式についてはこちらを参照してください。
定常波を考えるため、振幅 $A$ 、波長 $\lambda$ 、振動数 $f$ の全く同じ波が左右からやってきてぶつかることを考えます。
波の進む速さ $v$ は $v=f\lambda$ なので同じです。
図の青い波の式を、 $y_1=A\sin 2\pi f\left(t-\dfrac{x}{v}\right)$ 、オレンジの波の式を $y_2=A\sin 2\pi f\left(t+\dfrac{x}{v}\right)$ とします。

そうすると、それらの合成された波の変位を $y$ とすると、重ね合わせの原理から、
$y=y_1+y_2$
$~~=A\sin 2\pi f\left(t-\dfrac{x}{v}\right)+A\sin 2\pi f\left(t+\dfrac{x}{v}\right)$

したがって、
$y=A\sin 2\pi f\left(t-\dfrac{x}{v}\right)+A\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
$~~=A\times 2 \sin\dfrac{2\pi f\left(t-\dfrac{x}{v}\right)+ 2\pi f\left(t+\dfrac{x}{v}\right)}{2}\:\cos\dfrac{2\pi f\left(t-\dfrac{x}{v}\right)- 2\pi f\left(t+\dfrac{x}{v}\right)}{2}$
$~~=2A\sin (2\pi ft ) \cos \left(- 2\pi f \dfrac{x}{v}\right)$
$\cos(-\theta)=\cos\theta$ より、
$y=2A \sin (2\pi ft ) \cos \left(2\pi f \dfrac{x}{v}\right)$
ここで、 $F(x)=2A\cos \left(2\pi f \dfrac{x}{v}\right)$ $G(t)=\sin (2\pi ft)$ とすると、上の式は
$y=2A \cos \left(2\pi f \dfrac{x}{v}\right)\sin (2\pi ft )$
$y=F(x)G(t)$
と示されます。(一般的な波の式は $y=Af(x,t)$ となっています)
この式の $F(x)$ に着目すると、 $\cos$ 関数の $F(x)$ のグラフは $x$ だけで決まり、時間 $t$ に無関係に描かれます。
たとえば次のようなグラフです。( 縦軸 $-2A \sim +2A$ の範囲)
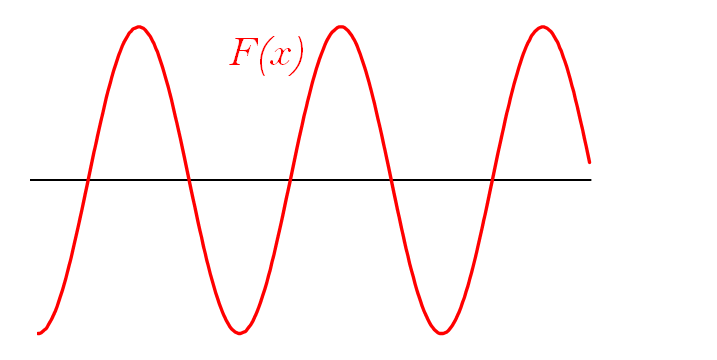
青とオレンジの波を合成したグラフ $y=F(x)G(t)$ はこの $F(x)$ に、時間の関数である $G(t)$ をかけることによって得られます。
ところで $G(t)$ は $\sin $ 関数ですから、その値は時間 $t$ により $-1 \sim +1 $ の範囲で変化します。
よって合成波の $y$ は、 $F(x)$ の値に $-1 \sim +1 $ の同じ数値を一律にかけて得られる、と考えられるため、合成波は下の図のようになります。
この合成波は $x$ 方向に進行せず、とどまっているように見えます。

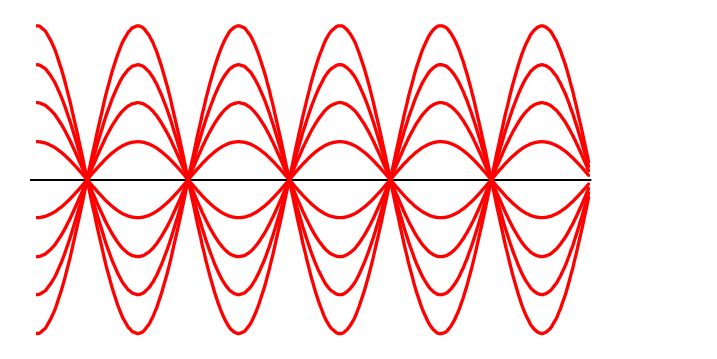
こういう波が定常波です。
定常波の波の式は上で示したように、
$y=2A\cos \left(2\pi f \dfrac{x}{v}\right)\sin (2\pi ft ) =2A \cos \left(2\pi \dfrac{x}{\lambda}\right)\sin \left(2\pi \dfrac{t}{T}\right)$
となります。( 右辺は $f=\dfrac{1}{T}$ および $v=f\lambda$ を用いて変形しています )
このとき、$|\sin (2\pi ft )| \leqq 1$ ですから、定常波の振幅は $2A$ です。
任意の点 $x$ における定常波の「振幅」は $\left|2A\cos \left(2\pi f \dfrac{x}{v}\right)\right|$ , $\left|2A\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|$ となります。
注意
ここでは簡単のため、青とオレンジの波に初期位相差がないものとしていますが、初期位相差 ( $\delta$ ) があっても基本的には同じことです。
たとえば、オレンジの波の式を $y_2=A\sin \left\{ 2\pi f\left(t+\dfrac{x}{v} \right)+\delta \right\}$ として計算すればよく、結論は変わりません。
計算してみると合成波は、
$y=2A \cos \left\{\left(2\pi \dfrac{x}{\lambda}\right)+\dfrac{\delta}{2} \right\} \sin \left\{ \left(2\pi \dfrac{t}{T}\right)+\dfrac{\delta}{2} \right\}$
が得られ、やはり $y=F'(x)G'(t)$ となりますから、定常波であるのは同じです。
ここで、任意の点 $x$ における定常波の「振幅」は $\left |2A\cos \left\{ \left(2\pi f \dfrac{x}{v}\right)+\dfrac{\delta}{2} \right\} \right |$ , $\left |2A\cos \left\{ \left(2\pi \dfrac{x}{\lambda} \right)+\dfrac{\delta}{2} \right\} \right |$ です。
よって、定常波の振幅の値は $\delta$ に関係なく $2A$ です。
腹の位置と間隔を求める
では、定常波の腹の位置を求めてみましょう。
定常波の波の式は次式で示されます。
$y=2A\cos \left(2\pi f \dfrac{x}{v}\right)\sin (2\pi ft ) =2A \cos \left(2\pi \dfrac{x}{\lambda}\right)\sin \left(2\pi \dfrac{t}{T}\right)$
腹では振幅が $2A$ となります。
任意の点 $x$ における定常波の「振幅」は $\left|2A\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|$ でしたから、腹の位置では、
$\left|2A\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|=2A$
より、 $\left|\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|=1$ となります。
ここで、$m$ 次の位置を $x_m$ とすると、腹の位置では $\left(2\pi \dfrac{x_m}{\lambda}\right)=m\pi$ となっていればいいですね。( $m$:整数 )

なぜならば、 $\cos(m\pi)=\pm 1$ だからです。
したがって、 $\left(2\pi \dfrac{x_m}{\lambda}\right)=m\pi$ より、
$x_m=\dfrac{1}{2}m\lambda$
腹と腹の間隔は $\Delta x$ ですから、
$\Delta x=x_{m+1}-x_m$
$~~=\dfrac{1}{2}(m+1)\lambda-\dfrac{1}{2}m\lambda$
$\Delta x=\dfrac{1}{2}\lambda$ となり、よく知られている「腹と腹の間隔は半波長」と一致します。
節の位置と間隔を求める
節の場合は、振幅が 0 になることから、
$\left|2A\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|=0$
より、 $\left|\cos \left(2\pi \dfrac{x}{\lambda}\right)\right|=0$ とすればよいことになります。
ここで、$m$ 次の位置を $x_m$ とすると、節の位置では $\left(2\pi \dfrac{x_m}{\lambda}\right)=\dfrac{\pi}{2}+m\pi$ となっていればいいですね。( $m$:整数 )

なぜならば、 $\cos\left(\dfrac{\pi}{2}+m\pi\right)=0$ だからです。
したがって、 $\left(2\pi \dfrac{x_m}{\lambda}\right)=\dfrac{\pi}{2}+m\pi$ より、
$x_m=\dfrac{2m+1}{4}\lambda$
です。
節と節の間隔は $\Delta x$ ですから、
$\Delta x=x_{m+1}-x_m$
$~~=\dfrac{2(m+1)+1}{4}\lambda-\dfrac{2m+1}{4}\lambda$
$\Delta x=\dfrac{1}{2}\lambda$ となり、(当然)腹と腹の間隔と同じです。
振幅の違う波の場合
問題
振幅,波長,振動数のうち振幅だけが違う場合(次図)は、どのような波が合成されるでしょうか。
選択肢から適当なものを選んでください。
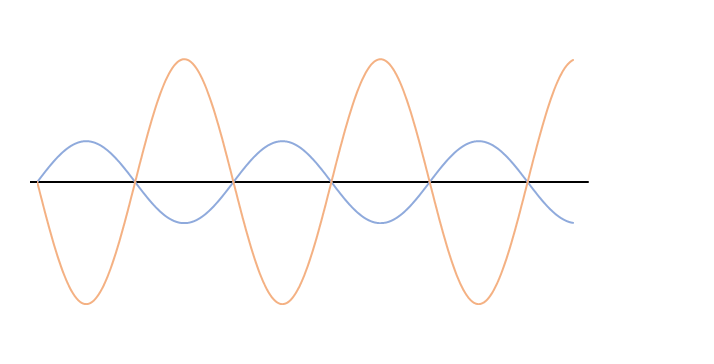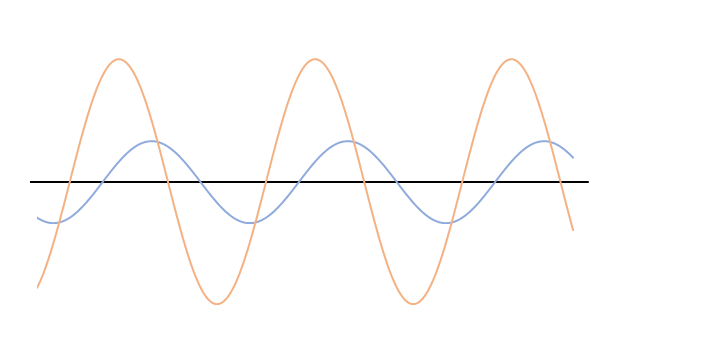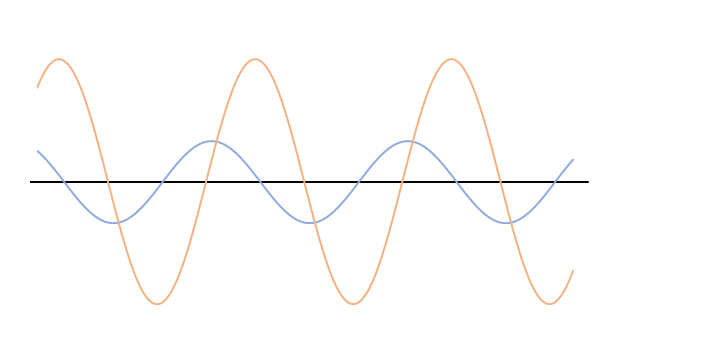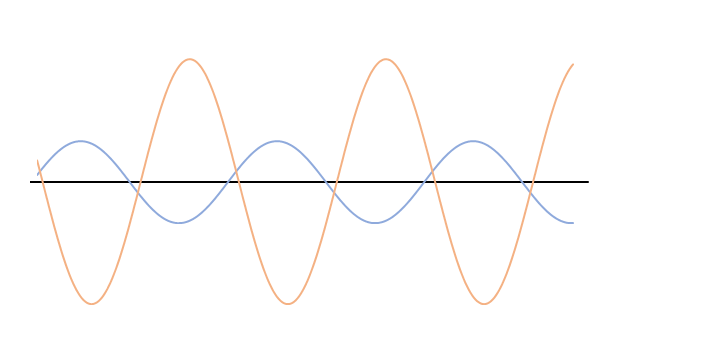
選択肢
- 振幅が違っても定常波は振幅が同じときと同様にできる
- 合成波の振幅が多少変化するが、左右に移動することのない定常波が生じる
- 振幅が違うと定常波とはならない

答え
答えは 3 の定常波とはならない・・・でした。
直感的には、合成波は、通常の定常波に比べて振幅が多少おかしくなるけど、左右に移動することは無い・・・のように思いませんか?
しかし、次のグラフをご覧ください。
ここでは、オレンジの波の振幅は青の波の振幅の1.5倍になっています。
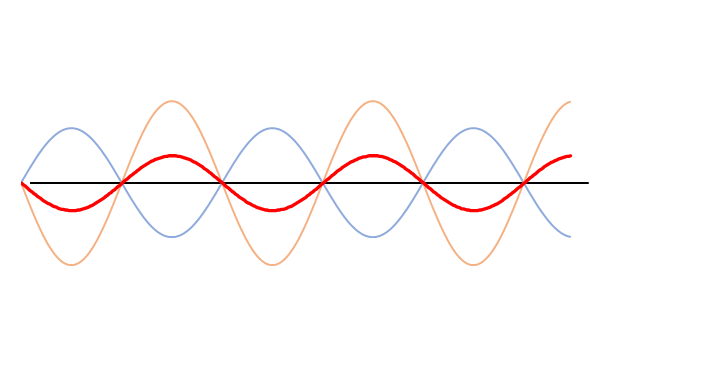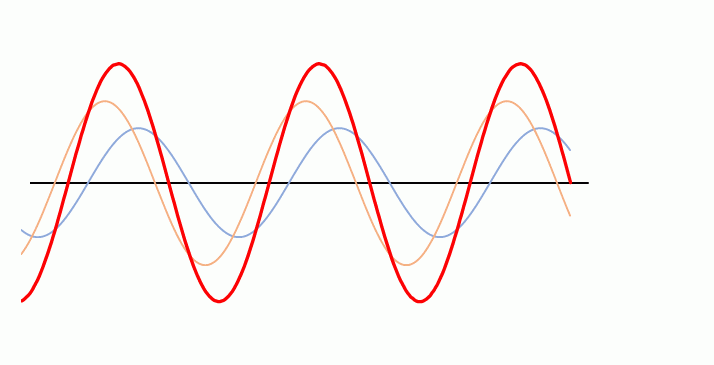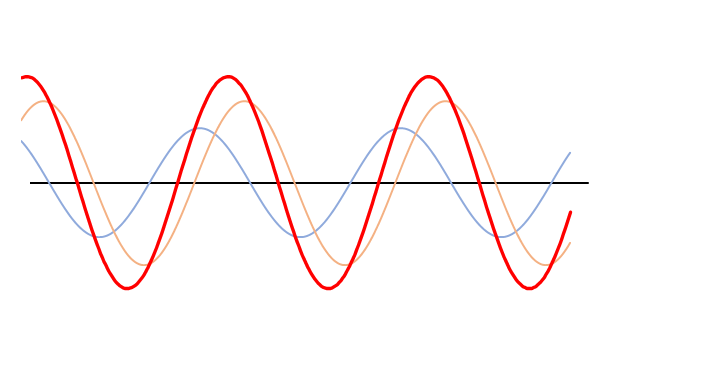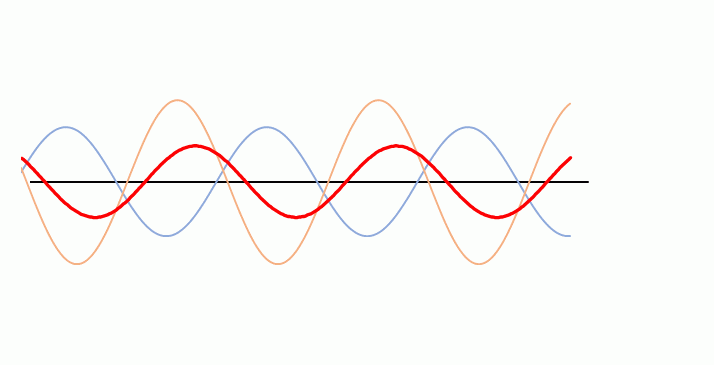
よく見ると合成波の赤い波は左に移動しています。
イメージで考える
こういう時は物理では極端な例を想像するとよいことが多いのです。
波長、振動数、速さが同じで振幅が異なる波が左右からやってきてぶつかる様子を考えます。
ここで例えば、青い波の振幅をほぼ 0 、オレンジの波の振幅を極端に大きくしてイメージしましょう。
そうすると、青の波の振幅が 0 に近いときは、ほぼノイズと考えてよいでしょうから、合成波は振幅の大きいオレンジの波とほぼ一緒の動きをするはず・・・ということに気が付きます。
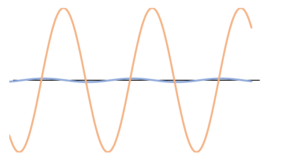
したがって、2つの波が左右からやってきてぶつかる場合、速さ、波長、振動数がおなじでも、振幅が違っていれば定常波にはならず、合成波は振幅の大きい波にひきずられるように進むだろう・・・という予測がつきます。
合成波の式
合成波の式を考えるため、波長 $\lambda$ 、振動数 $f$ が全く同じで、振幅だけが違う波が左右からやってきてぶつかることを考えます。
波の進む速さ $v$ も $v=f\lambda$ なので同じです。
図の青い波の式を、 $y_1=A_1\sin 2\pi f\left(t-\dfrac{x}{v}\right)$ 、オレンジの波の式を $y_2=A_2\sin 2\pi f\left(t+\dfrac{x}{v}\right)$ とします。
( 振幅 $A_1$ , $A_2$ )

そうすると、それらの合成された波の変位を $y$ とすると、重ね合わせの原理から、
$y=y_1+y_2$
$~~=A_1\sin 2\pi f\left(t-\dfrac{x}{v}\right)+A_2\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
ここで、 $A_2=kA_1$ とします。( $k$:定数 )

したがって、
$y=A_1\sin 2\pi f\left(t-\dfrac{x}{v}\right)+A_2\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
$~~=A_1\sin 2\pi f\left(t-\dfrac{x}{v}\right)+A_1\sin 2\pi f\left(t+\dfrac{x}{v}\right)+(k-1)A_1\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
$~~=A_1\times 2 \sin\dfrac{2\pi f\left(t-\dfrac{x}{v}\right)+ 2\pi f\left(t+\dfrac{x}{v}\right)}{2}\:\cos\dfrac{2\pi f\left(t-\dfrac{x}{v}\right)- 2\pi f\left(t+\dfrac{x}{v}\right)}{2}$
$~~\quad\quad +(k-1)A_1\sin 2\pi f\left(t+\dfrac{x}{v}\right) $
$~~=2A\sin (2\pi ft ) \cos \left(- 2\pi f \dfrac{x}{v}\right)+(k-1)A_1\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
$\cos(-\theta)=\cos\theta$ より、
$y=2A\sin (2\pi ft ) \cos \left(2\pi f \dfrac{x}{v}\right)+(k-1)A_1\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
$A_2=kA_1$ を戻すと、
$y=2A\sin (2\pi ft ) \cos \left(2\pi f \dfrac{x}{v}\right)+(A_2-A_1)\sin 2\pi f\left(t+\dfrac{x}{v}\right)$
この式の左辺の前半部分は、前項で扱ったものと同じ定常波を示します。
しかし、式の後半部分では進行波を示す $y=Af(x,t)$ の形となっています。
このため、合成波が時間とともに移動することを示しています。
補足:三角関数
$\sin(\alpha+\beta)=\sin\alpha \cos\beta +\cos\alpha \sin\beta$
$\sin(\alpha-\beta)=\sin\alpha \cos\beta -\cos\alpha \sin\beta$
辺々足して、
$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha \cos\beta$
$\alpha+\beta=A$ $\alpha-\beta=B$ とおきます。
そうすると、
$\alpha=\dfrac{A+B}{2}$ $\beta=\dfrac{A-B}{2}$
したがって、これらを
$\sin(\alpha+\beta)+\sin (\alpha-\beta)=2\sin\alpha \cos\beta$
へ代入すると、
$\sin A+\sin B=2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$
が得られます。




































コメント