回折格子
ヤングの実験で光の回折・干渉について扱ってきました。
ヤングの実験の発展形として、回折格子について解説します
回折格子はガラスなどの表面に非常に細かい筋を引いたもので、$1\:\mathrm{cm}$ あたり数百本から数千本もの筋を引いてあります。
これらの筋を引いたところは光を通さず、削られず残ったところがヤングの実験におけるスリットの役割をし、回折・干渉を起こします。
つまり、イメージとしては、たくさんのスリットのあるヤングの実験装置でよいでしょう。
光源としては普通はレーザー光を使います。
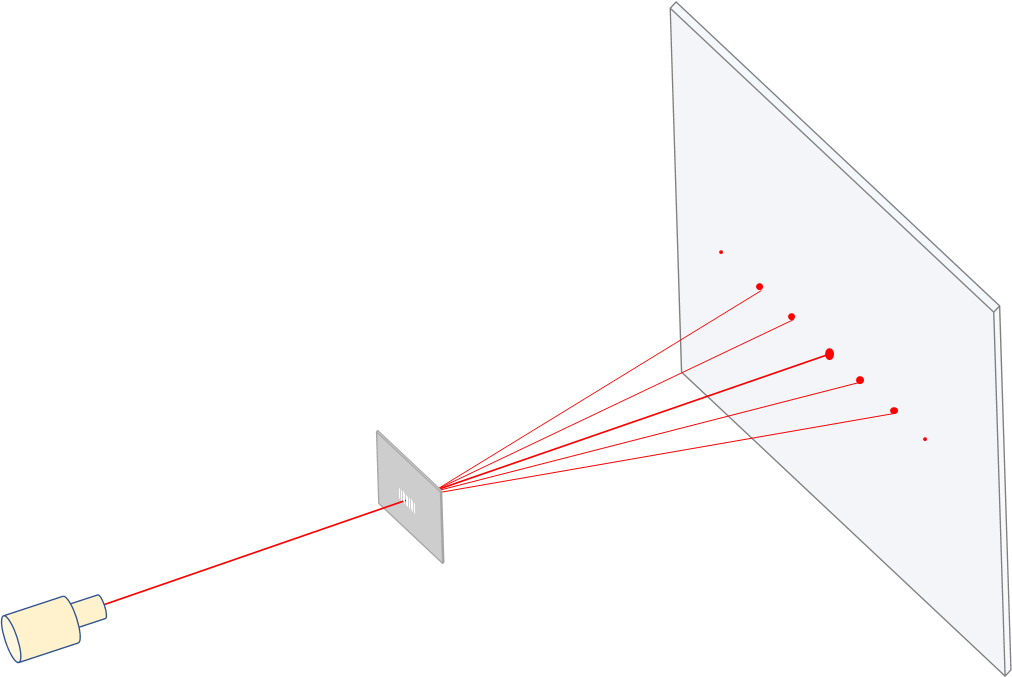
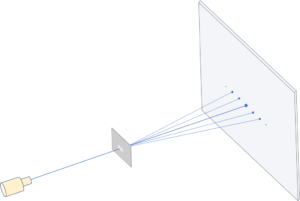
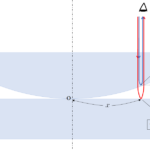
回折格子を使うと、図のようにスクリーン上に非常に明るくするどい輝点を生じます。
これは回折格子が非常に多数のスリットからできているためです。
ヤングの実験の、ぼんやりした明暗の干渉縞とは決定的に違う点です。
では回折格子の断面を見てください。
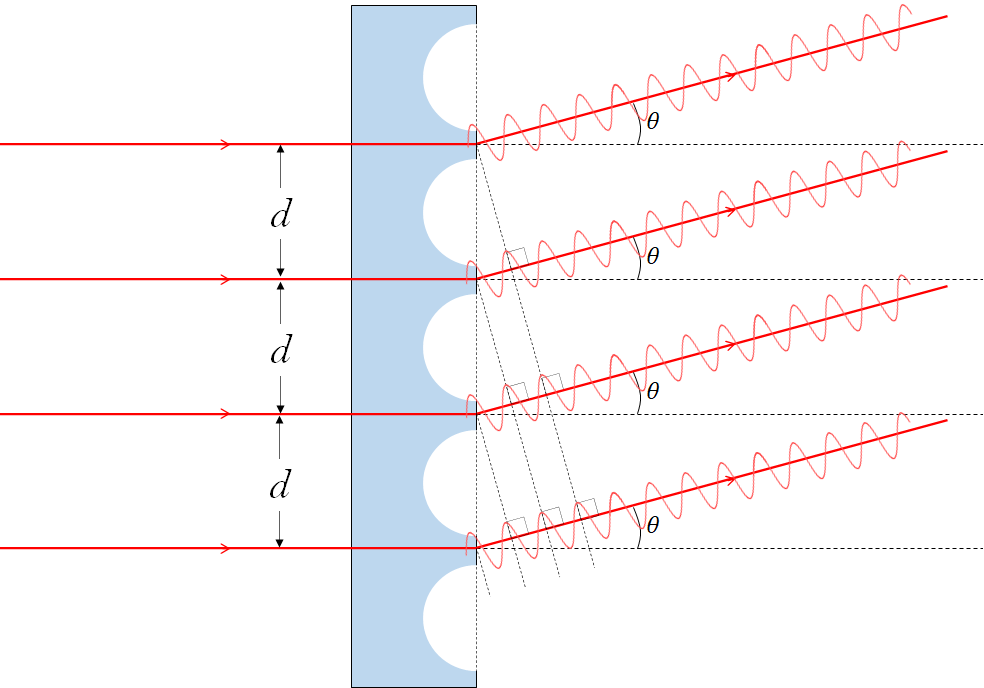
ガラス面の傷の筋のところを通った光は
拡散してしまうので、光が透過できません。
そのため、ガラス面の削られずに残ったところが
スリットとして機能します。
明線条件
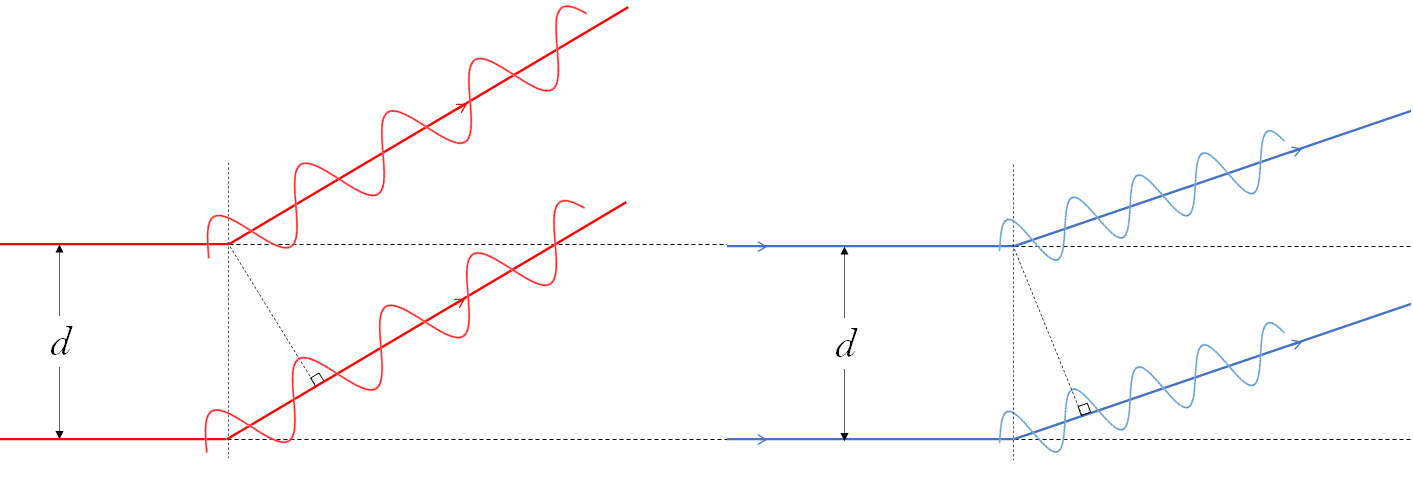
このとき、隣り合うスリットの回折光は $d\sin\theta$ だけ経路差が生じます（次図参照）。
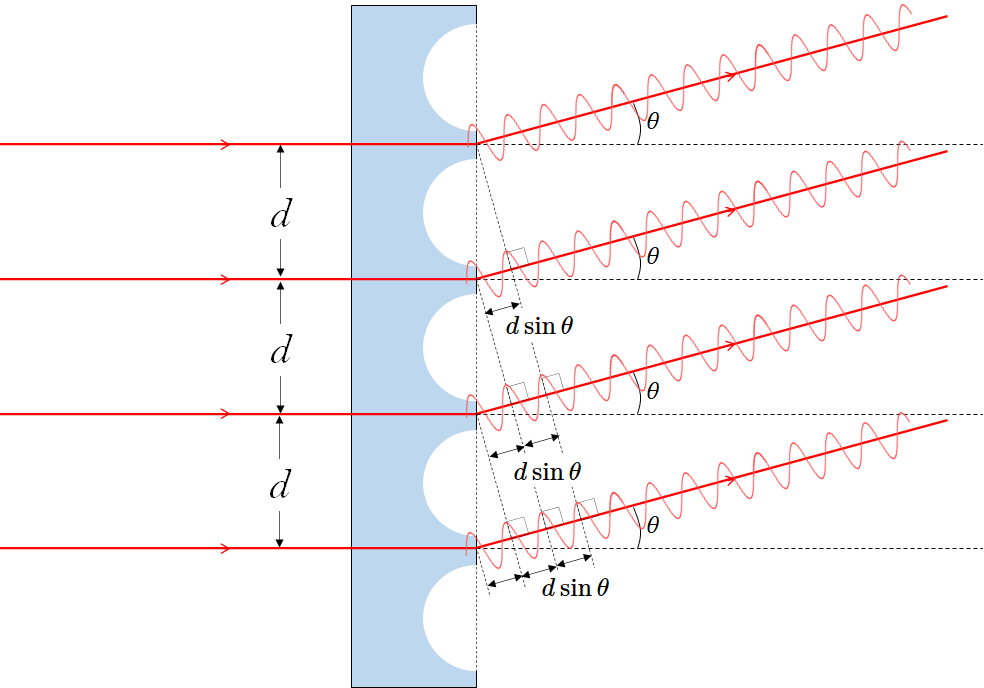
したがって、ヤングの実験の式と同様に、輝点（明点）を生じるには、
経路差 $d\sin\theta$ のなかに整数倍の $\lambda$ が入ればよいことになります。
よって、
明線 ： $d\sin\theta = m\lambda$
( $m=0,\:,\:1,\:2,\:3,\:\cdots\cdots$ )
が成り立ちます。
暗線条件
回折格子の作る輝点の間は広くあいていてスカスカです。
回折格子では暗線条件は考えません。
これはなぜでしょうか。
非常に多数のスリットからの回折光が集まるため、すべてのスリットからの回折光の位相がぴったり合うところ（輝点）以外では、多数の回折光の位相が少しずつずれてしまうため弱めあい、明るくならないのです。
では次に問題をやってみましょう。
問題 レーザー光を赤から青にするとどうなるか
レーザーを赤から青に変えてみましょう。
この時、スクリーン上の輝点の間隔は？
- 広くなる
- 狭くなる
答え
答え 狭くなる
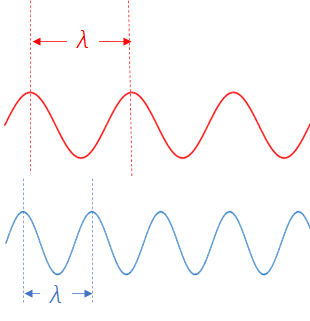
これはなぜでしょうか。
光の波長を考えてみます。
赤色の波長 ＞ 青色の波長
です。
輝点を生じるためには隣どうしのスリットから出る光の経路差が、一次光では $d\sin\theta = \lambda$ である必要があります。（$m=1$ の場合）
青色の光の波長は赤に比べて短いため、条件を満たす角度 $\theta$ は赤色の時よりも小さくて済むのです。
問題 白色光をあてるとどうなるか
単色光の代わりに白色光を用いるとスクリーン上ではどのような現象がおこるでしょうか。
答え
白色光はいろいろな波長の光を含みます。
そのため、各色が強め合う角度はまちまちになり、スクリーン上は色づいて見えることになります。
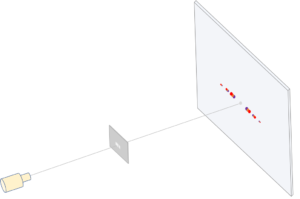
その際、中心に近いほうが波長の短い青や紫で、中心から遠いほうが波長の長い赤色になります。
つまり、回折格子を用いれば光を分けることが可能になります。
こういった装置を分光器とよび、物理光学上重要な機器です。
コメント