
Alexas_Fotos / Pixabay
ラジアン角を知っていますか?多くの人は数学の授業で習ったはずです。
しかし、ラジアンになぜ π がつくの?とたずねてみても明確な答えはありません。
そう習ったから・・・ そう決めたから・・・ とあいまいです。
もし、上の問いに戸惑うならば、あなたもラジアンをもう一度考えてみませんか?
角度を示そう
まず角度でよく使われる、度 ° です。円を 360 分割したものが、1° ですね。
この 360 は1年が 365 日なので、それに近い数字を取ったようです。
これはこれで直感的にわかりやすい決め方ですね。
でももっと便利な方法を思いついたのです。
それが弧度法(ラジアン角)です。これはいったいどのようにして角度を決めているのでしょうか?またどうして角度なのに円周率 $\pi$ がつくのでしょうか?
ラジアンについては、いろいろなサイトでいろいろな説明がされていますがここでは実戦的に考えます。
ラジアンとは?
半径 1 の円を考えましょう。これを単位円といいます。
単位円の円周長さは $2\pi \times 1= 2\pi $ ですね。
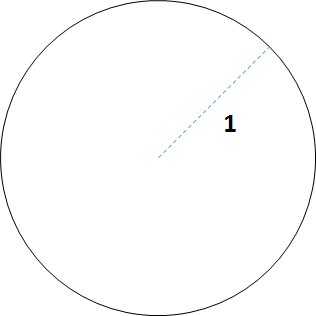
この単位円上で、ある角度で切り取った円弧の長さを考えましょう。
このとき、この中心角に対応する円弧の長さは一つしかありません。
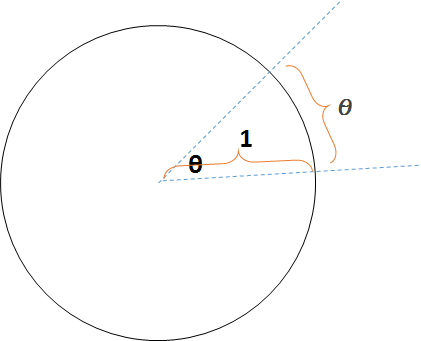
このとき、この角度 $ \theta $を、単位円において対応する円弧長さで示そうというアイデアが弧度法・ラジアンです。
すなわち、半径が 1 なので一周は $2\pi $ ですが、その円弧長さ(一週長さ)を使って $360°$ を $2\pi \: [rad] $ とします。
そうすると $90°$ はその $\dfrac{1}{4}$ なので、$ 2\pi \times \dfrac{1}{4} = \dfrac{\pi}{2} \:[rad]$ というわけです。これはすべて半径 1 の円での話です。
逆に言えば、
$\dfrac{\pi}{2}\:[rad]$ は半径 1 の円において、円弧長さが $\dfrac{\pi}{2}$ になるような角度である・・・・すなわち 90° であるということですね。
では、以下の問題をやってみましょう。
すべてラジアンに直してください。
$ 270° = $
$ 60° = $
$ 45° = $
$ 30° = $
$ 270° =2\pi \times \dfrac{270°}{360°}=\dfrac{3\pi}{2}\:[rad]$
$ 60° =2\pi \times \dfrac{60°}{360°}=\dfrac{\pi}{3}\:[rad]$
$ 45° =2\pi \times \dfrac{45°}{360°}=\dfrac{\pi}{4}\:[rad]$
$ 30° =2\pi \times \dfrac{30°}{360°}=\dfrac{\pi}{6}\:[rad]$
となります。これで $\pi$ がつく理由がお分かりでしょうか。
でもなぜこんなことをするのでしょうか?
ラジアンの有用性
ラジアンにする一番の理由はその有用性です。
もう一度定義を見ましょう。
ラジアンとは半径1(単位円)のある角度で切り取られる円弧長さで角度を示そう!でしたね。
ということは、半径が2であるなら対応する円弧長さも2倍になるのです。
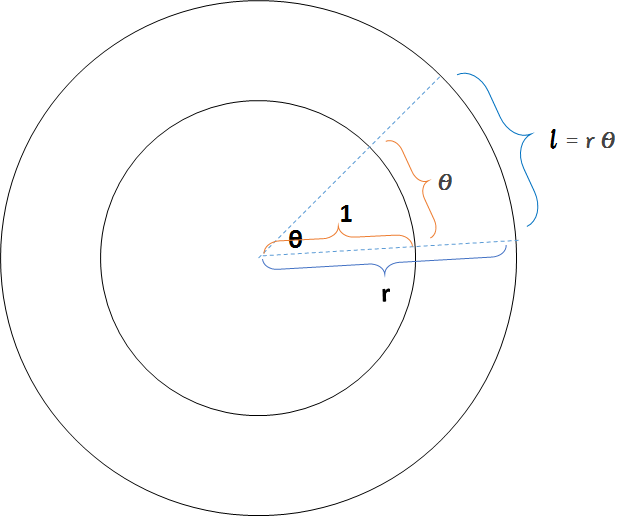
すなわち、半径が $r$ のときの円弧長さ $l$ はその角度 $\theta \:[rad]$ を使って $r\times\theta $ となるはずです。
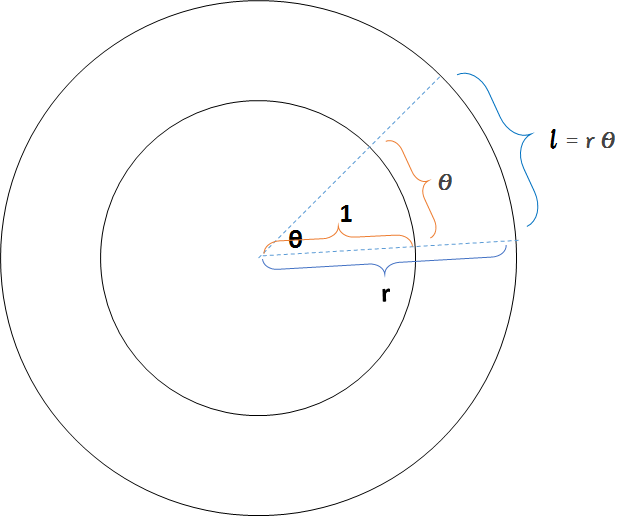
すなわち、
$$ l = r \theta $$
角度をラジアンで示しておくことで、対応する円弧長さがすぐに出ること、これがラジアンを使う大きな理由です。
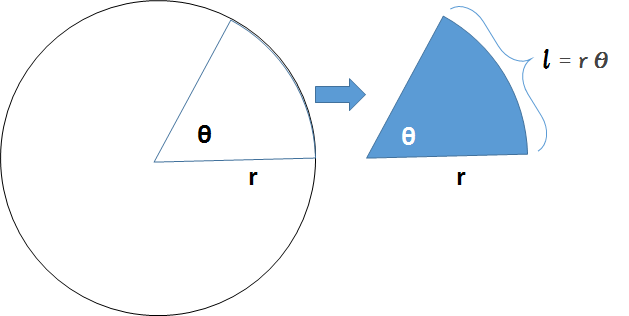
そうすると、次のことが簡単にできます。
答え
$ l= r\times\theta = 5\times \dfrac{\pi}{3} $
どうです?簡単ですね。物理の等速円運動・単振動・波動ではこのラジアンが威力を発揮します。





































コメント