慣性力
慣性力とは、加速する系において考える補正項で、その大きさは $ma$、方向は系の加速度と一直線上逆向きです。
これは、直線運動でも回転運動でも、どのような運動でも成り立ちます。
よくにた言葉の響きである、慣性の法則は次の記事で扱っています。

等速直線運動

電車が一定速度で走っているときは、電車の中に吊り下げられたおもりは、電車内の人から見て鉛直に垂れ下がって静止しています。
この様子は電車が、駅で静止しているときと変わりません。
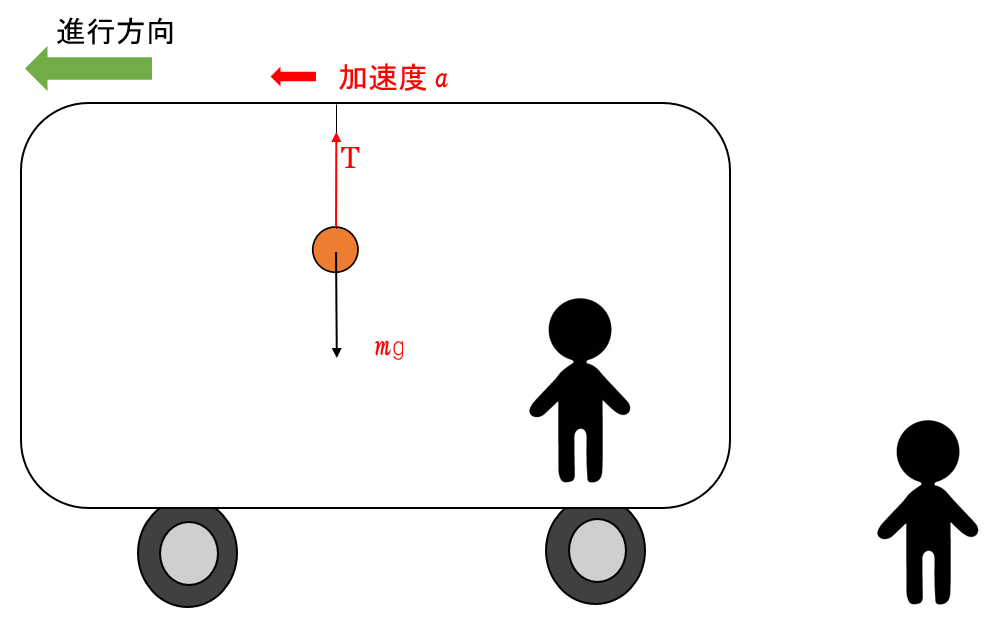
また、等速直線運動する車内(慣性系)で、物体を落としても自由落下するでしょう。
これらは、等速直線運動する車内で観察する人にとっても、静止の状態と同じ物理法則が成り立つことを示しています。
でないと、飛行機内や新幹線車内でお弁当を食べたり、歩き回ったりするなど、とんでもない行為になります。
加速する車内
電車が加速運動(急発進や急停止中)しているときはどうでしょうか。
もしも、急発進したり急停止したりしている車内でお弁当のおかずを落としたりすると、飛んで行ってしまうはずです。
では、加速する電車内につり下げられた物体の運動について、考えてみましょう。
運動方程式
加速度 $a$ で運動する電車内の様子を次図に示します。
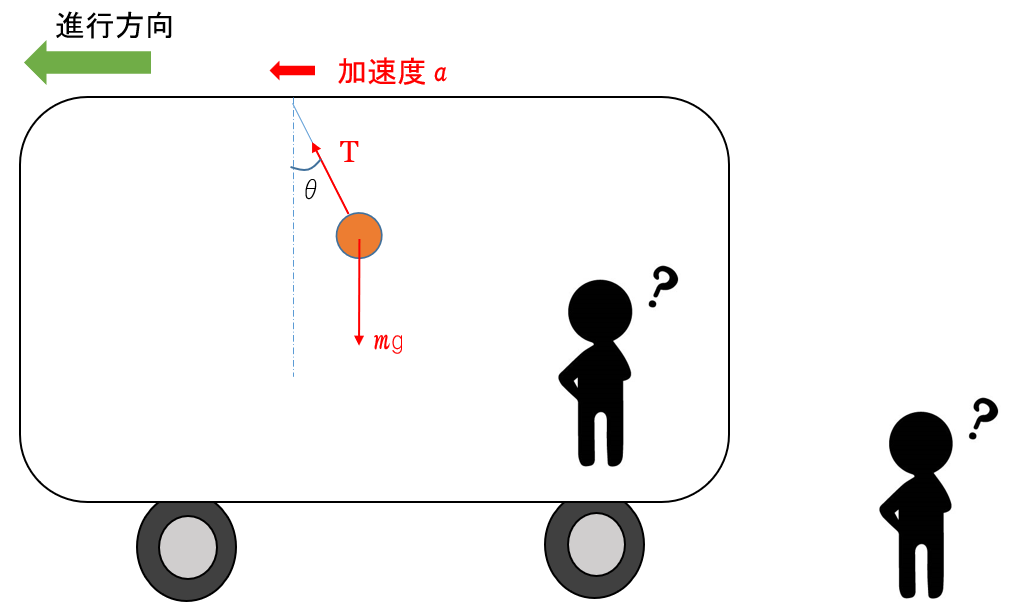
理想的な状況下で、おもり(質量 $m$ )が鉛直線とある角度 $\theta$ をなしているように見えたとしましょう。
この時のおもりについての物理的な説明は、「張力 $T$ と重力 $mg$ の合力である $F= mg\tan\theta $ の大きさの力が水平な加速度方向に向いており、おもりに水平方向の加速度をもたらしている」というわけです。
(このときのおもりの加速度 $a$ は電車の加速度と一致します)
したがって、ニュートンの運動方程式 $ma=F$ より、
$ma=mg\tan \theta$
が成り立ちます。
あるいは、張力 $T$ を鉛直方向と水平方向に分解してみます。
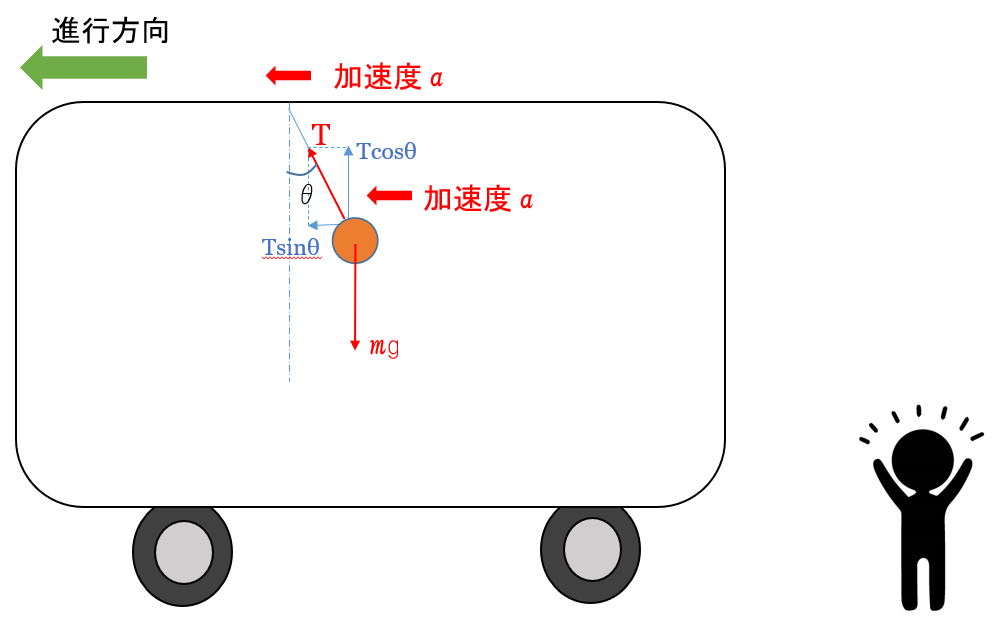
そうすると、水平方向には加速度 $a$ を持ち、鉛直方向は重力とつり合っていると考えられます。
水平方向には運動方程式を、鉛直方向にはつり合いの式(加速度 0 の運動方程式)を書くと、
水平方向 $T\sin \theta=ma$
鉛直方向 $T\cos \theta -mg=0$ より $T\cos \theta =mg$
の式が成り立ちます。
これらを辺々割ります。
$\dfrac{T\sin \theta }{T\cos \theta}=\dfrac{ma}{mg}$
これより、$ma=mg\tan\theta=F $ が成り立ちます。
ここで、大事なことですが、ニュートンの運動の法則によると、必ず加速度 $\vec{a}$ の方向に合力 $\vec{F}$ がはたらきます。$m\vec{a}=\vec{F}$
慣性力
ではここで、考え方を変えてみます。
もう一度加速する電車内につるされた物体を観察します。

このとき、電車内に乗っている人の見方を考えます。
等速直線運動する電車に乗る人にとっては、電車内での物理法則は電車が駅で停止している場合と同じです。
しかし、加速する電車の車内の人が見ると、天井からつるされた物体は斜めに傾いて静止しているわけですから、停止しているときと同じ物理法則が成り立ってはいません。
そこで、この加速する電車内から観測する人にとっても、物理法則を成立させるような仕掛けを考えてみます。
慣性力の方向
そのために、天井からつるされて傾いている物体に、張力と重力の合力と一直線上反対向きの力がはたらいていると考えてみましょう。補正項を考えるということですね。
そうすると、物体にはたらく力がつり合いの状態になり(図)、車内の人から見て、物体が静止していることの説明ができます。
つまり、この補正項を考えることで、電車内で観測する人にとっても、物理法則が成り立つと考えることができます。
この新たに考える力は、必ず電車の加速度の向きと一直線上逆向きになります。
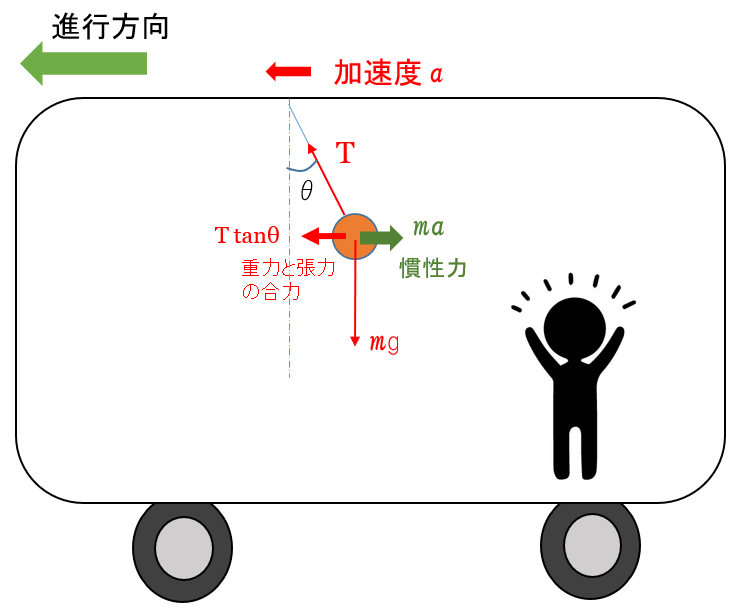
これが慣性力の意味です。
慣性力の大きさは?
では、その加速度と反対向きにはたらく力の大きさは、いくらにすればよいでしょうか?
さきほど、電車外から見た人は、電車の加速度の方向に物体には $F=mg\tan\theta$ の合力がかかっているように見えたはずです。
したがって、電車内から見て物体がつり合うためには、電車の加速度と反対方向に $F’=mg\tan\theta$ の大きさの力がはたらけばよいことになります。

この $F’=mg\tan\theta$ の大きさは、さきほどの結果から $ma$ と示せます。
したがって、慣性力 $F’$ の大きさは電車の加速度 $a$ を使って書けば、$F’=ma$ で示されます。
つまり、慣性力とは、電車の加速度方向と真逆に $ma$ の力を考えてやればよいのです。
慣性力
系の加速度 $a$ と一直線上反対向きにはたらく大きさ $ma$ の力を慣性力という。
慣性力は、加速する系から観測するすべての物体にかかると考えられる。

加速する系(非慣性系)から観測するすべての物体に慣性力がかかります。
例えば、電車内の物体だけではなく、電車の窓から見える人やビルなど、全てのものにも慣性力がかかるのです。
遠心力
慣性力は、系の加速度 $a$ と一直線上反対向きに $ma$ であり、どのような加速系(非慣性系)においても成り立います。
したがって、回転する系においても慣性力が考えられ、回転の加速度 $a$ と真逆に $ma$ です。
これが遠心力 $ma$ です。
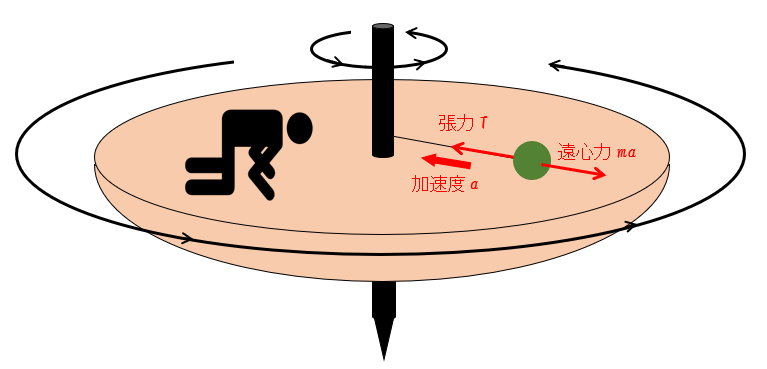
よく、慣性力は $ma$ 、遠心力は $m\dfrac{v^2}{r}\:\:\:\cdots$ などと念仏のように唱えている人を見かけますが、これら両者は同じ慣性力です。
したがって、遠心力も回転系の加速度と逆向きに $ma$ とするだけです。
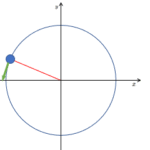
等速円運動している場合の加速度 $a$ は、回転の中心に向いています。
よってこの場合の遠心力は回転中心から外側へ向き、大きさは $ma$ です。
等速円運動については、等速円運動を参照してください。
物理クイズ
さて、慣性力のお話の最後に、次のクイズを考えてみてください。
問題
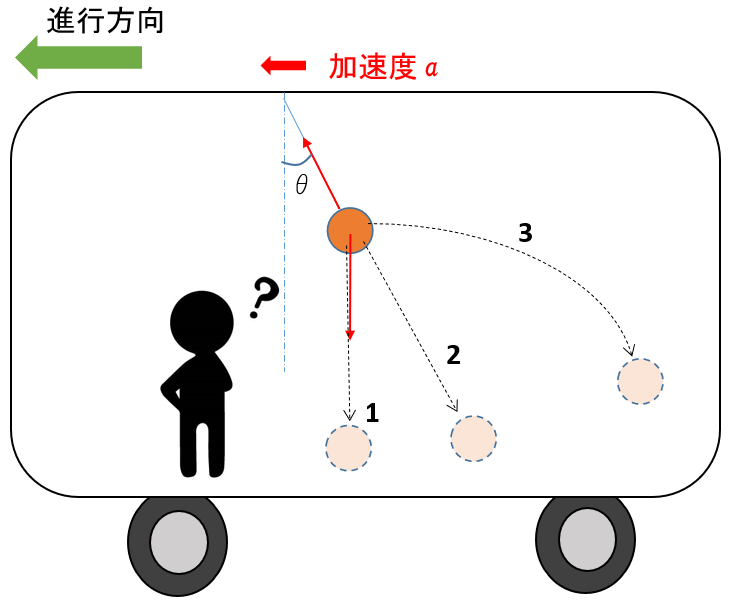
図のように、運動している電車の車内におもりをつるしています。
電車が加速運動しているときに、とつぜん物体をつないでいる糸が切れてしまいました。
その後の物体の運動は、電車内から見て、図の (1) (2) (3) のどれでしょうか?
また、電車がから見ると、物体はどのように見えるのでしょうか?
答え
加速する電車内の人が見る場合は、観測するものすべてに慣性力がかかります。
したがって、糸が切れて空中にある物体にも慣性力がかかっているのです。
電車内の人から見て、物体には重力と慣性力である $ma$ がかかっています。
糸が切れると、この慣性力と重力の合力の方向に「落ちて」行きます。
したがって、答えは図の (2) です。
つまり、電車内の世界では右斜め下が「真下」ということになります。
しかし、電車外の人から見ると、糸が切れた後の物体は重力を受けているだけですから、電車の進行方向に水平投射をしたように見えます。
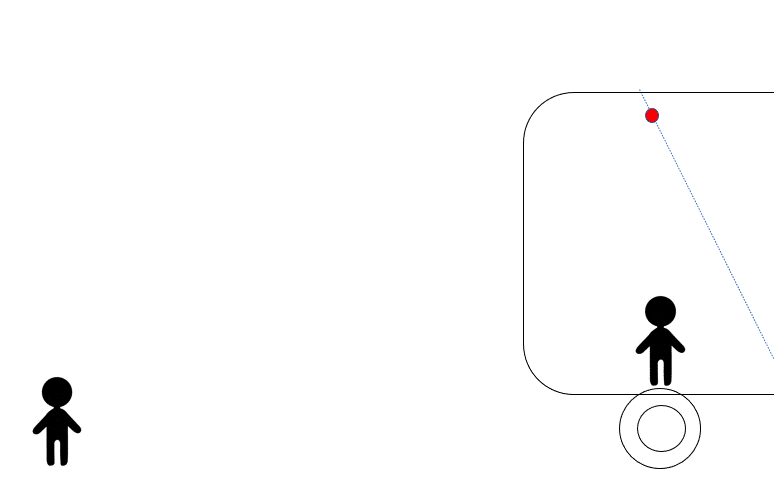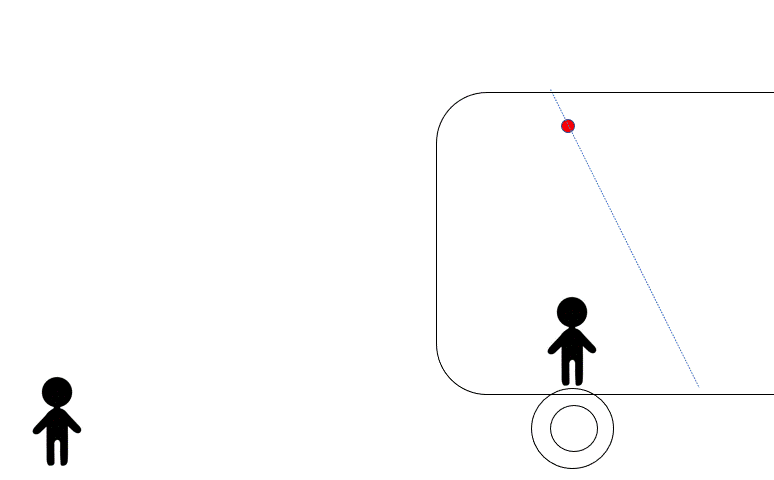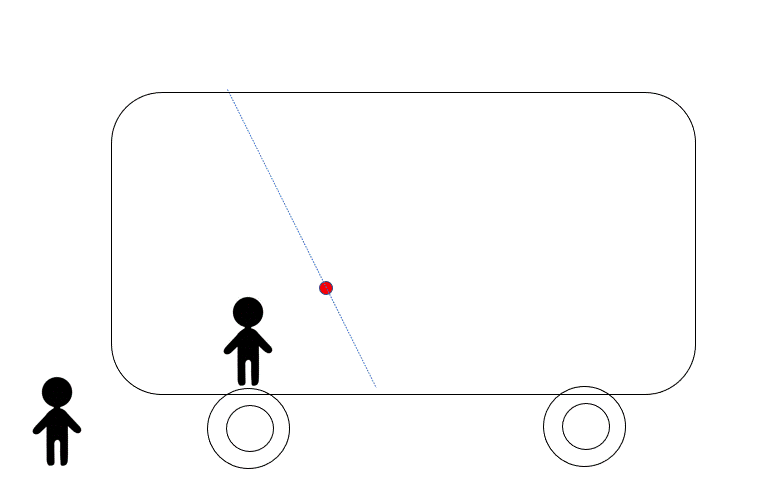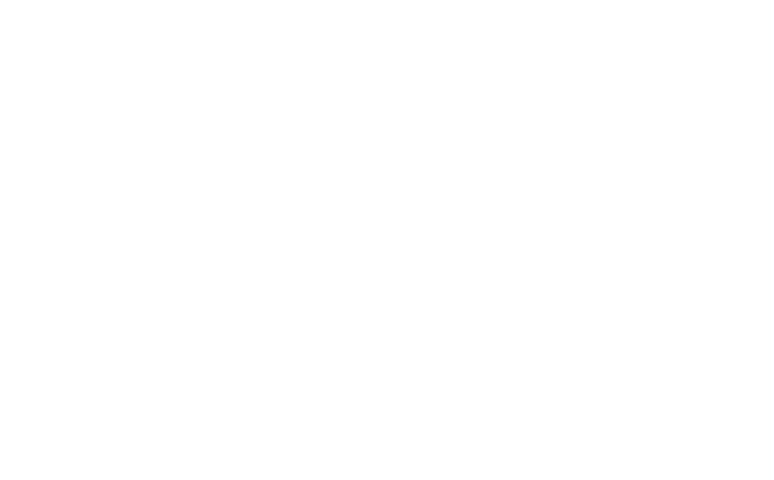
こちらのクイズもぜひチャレンジを
まとめ
慣性力はどのような場合も、迷わずに、系の加速度 $a$ と一直線上逆向きに $ma$ です。
糸でつながれていようがなかろうが、電車内であろうがなかろうが、観測するものすべてに慣性力がかかります。
慣性力を使えば、簡単に問題を解くことができる場合も多くなります。
例えばコレ
こちらの記事も参考に!エレベーターの加速運動について考察しています。
絶対にマスターしましょう。




































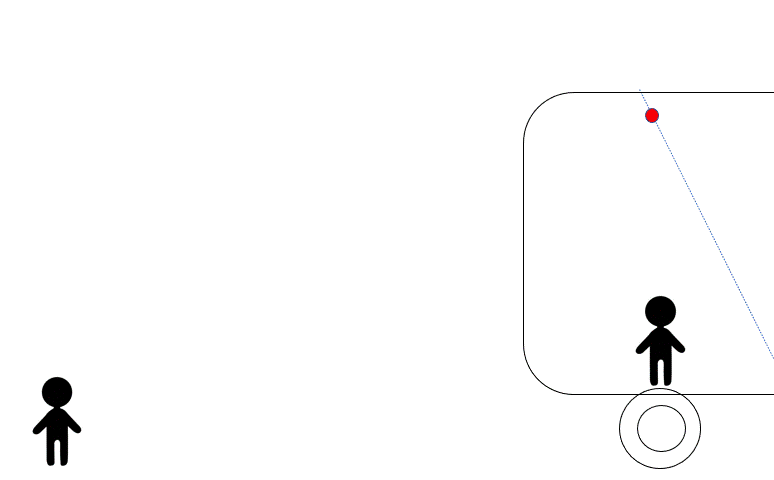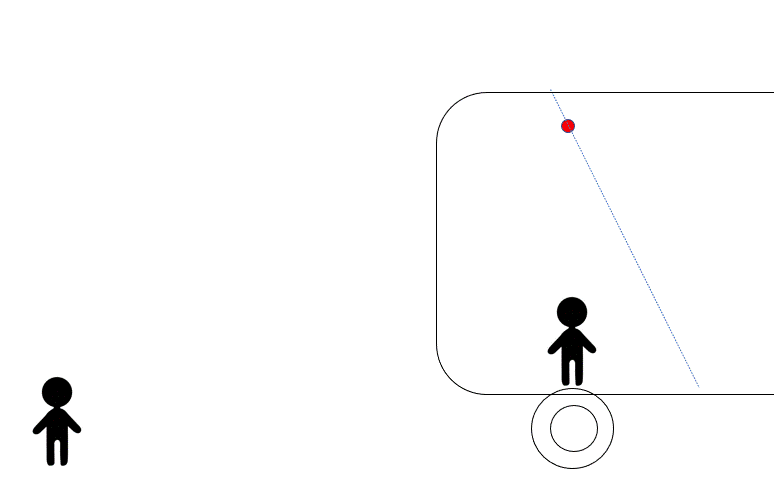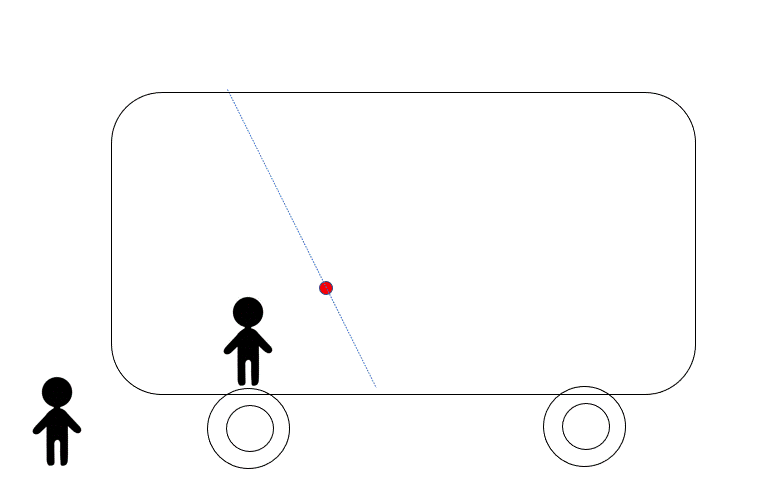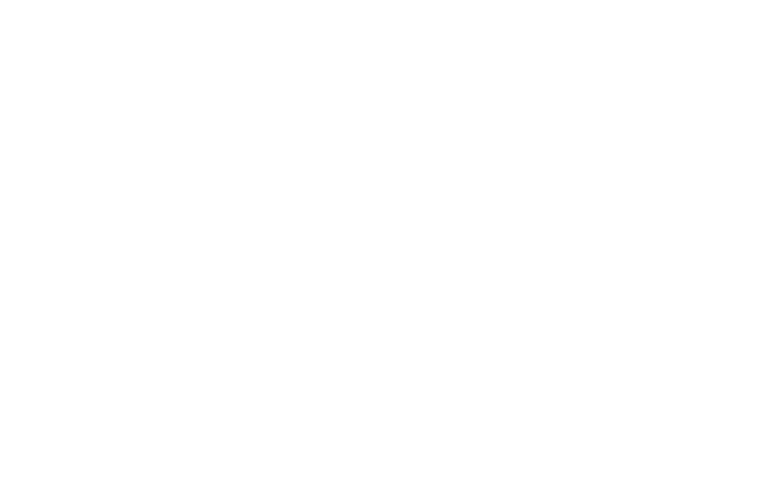
コメント