単振り子とばね振り子

単振り子とばね振り子

まずは、単振動の復習をしましょう。

単振動

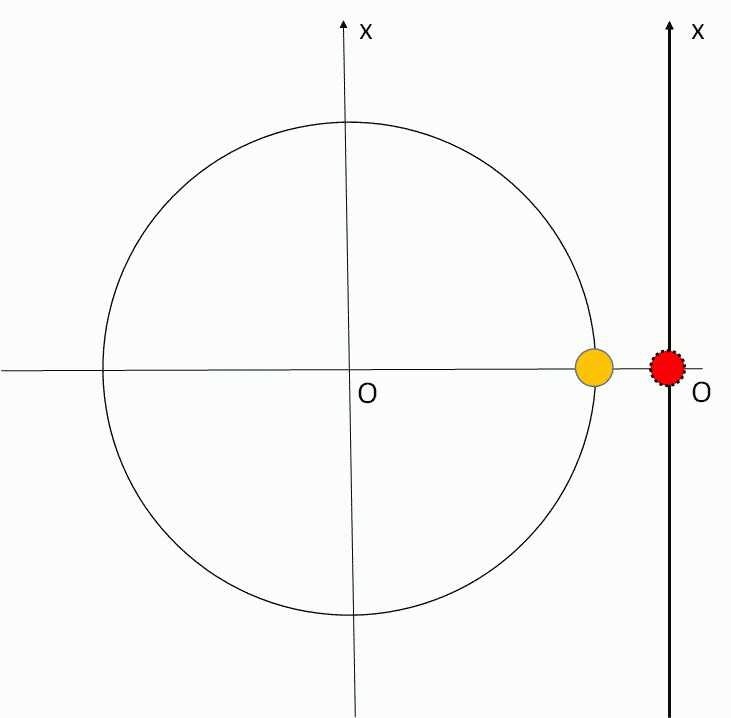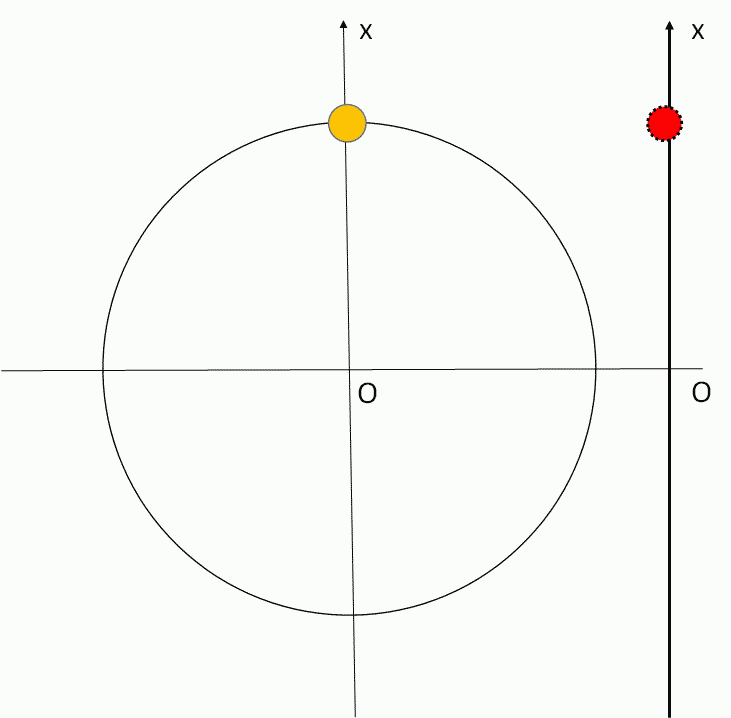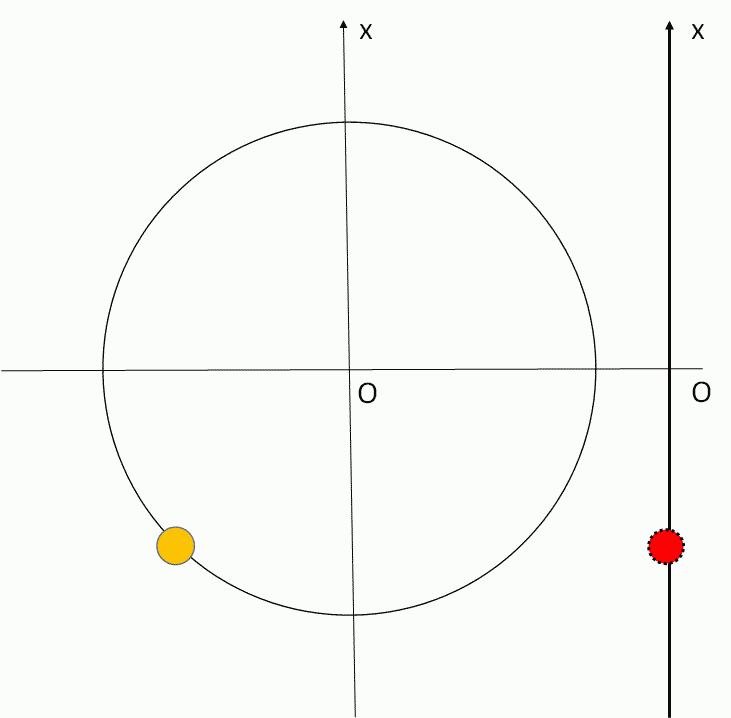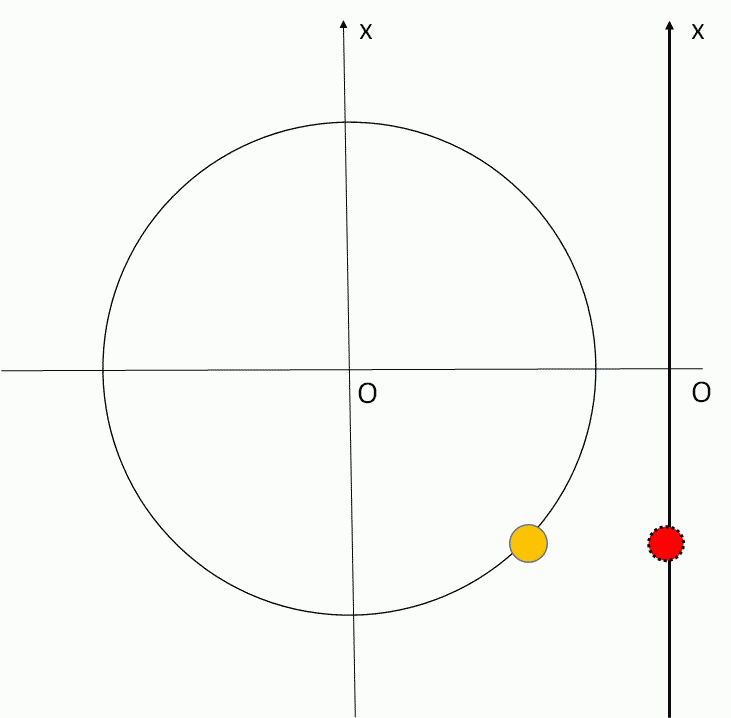
$f=\dfrac{1}{T}$ $\:\:\:\:\:\:\:\:$ $\omega=\dfrac{2\pi}{T}=2\pi f$ $\:\:\:\:\:\:\:\:$ $T=2\pi \sqrt{\dfrac{m}{k}}$

$x=A\sin \omega t$ $\:\:\:\:\:\:\:\:$ $v=\dfrac{dx}{dt}=A\omega\cos \omega t$ $\:\:\:\:\:\:\:\:$ $a=\dfrac{dv}{dt}= -\omega^2 x $

$F=ma= -m\omega^2 x $

単振動の基本的な事項については以下の記事をご覧ください。

単振動を理解するには等速円運動の知識・理解が不可欠です。

YouTube 動画解説 等速円運動 単振動

この等速円運動と単振動は密接につながっています。 単振動をきちんと理解しようと思ったら、等速円運動の理解は必須なのです。 まずは、等速円運動をしっかり理解してください。 そして、等速円運動と単振動は後の波動の原理の理解に必要不可欠なのです。...

kokolainen.com

微積を使って、単振動の式を導出する方法を覚えておくと便利です。

単振動の式を導く！微積を使えばもう暗記しなくても良い

単振動を苦手とする人は多いようです。 また、教科書ではわりとサラリと済ませているので、入試問題になると手が出なくなる人も多く見かけます。 確かに入試では割と難しい問題が出るように思いませんか？ 単振動については、問題集でやり込む必要がありま...

kokolainen.com

単振り子

単振り子とは、図のような単純な振り子です。
この振り子が、振れ幅が小さく、鉛直面内で運動する場合を考えます。

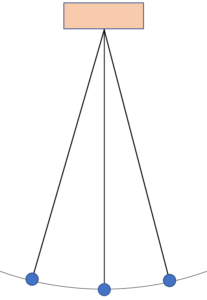
図で、糸の長さを $l$ 、つるしている物体の質量を $m$ としましょう。

このとき、静止している人から見て、物体にはたらく力は、重力 $mg$ と糸の張力 $S$ だけです。

今、図のように、鉛直線から角度 $\theta$ だけ、振り子が振れて運動している状態を考えます。

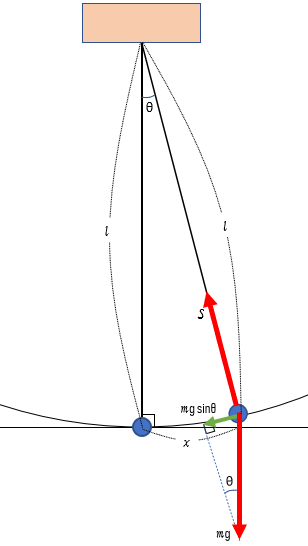
振れ角 $\theta$ が小さいので、運動の接線方向の力は $mg\sin \theta $ となります。

ここで、物体の位置を $x$ としてやると、ラジアン角 $\theta$ と円周の関係から、$x=l \theta $　より、$\theta=\dfrac{x}{l}$　です。

そうすると、この物体にはたらく力は　$F=-mg\sin \theta = -mg\sin \dfrac{x}{l}$　と示されます。

振れ角 $\theta$ が十分小さいとき、 $\tan \theta \fallingdotseq \sin \theta \fallingdotseq \theta$　とできますから、合力 $F$ は

$F=-mg\sin\dfrac{x}{l} \fallingdotseq -\dfrac{mg}{l}x$

が成り立ちます。
これは、$k=\dfrac{mg}{l}$　とおけば、

$F=-\dfrac{mg}{l}x=-kx$

となり、単振動するという要件を満たします。
なので、振れ角 $\theta$ が小さいとき、単振り子は単振動するとみなせることになります。

ここで、単振動の関係から

$F=-kx=-m\omega^2x$

より、$k=m\omega^2$　となります。

したがって、$\omega=\sqrt{\dfrac{k}{m}}$　が得られます。

$\omega=\dfrac{2\pi}{T}$　であるため、$k=\dfrac{mg}{l}$　より、

$\omega=\sqrt{\dfrac{m}{k}}$

$T=2\pi\sqrt{\dfrac{k}{m}}=2\pi\sqrt{\dfrac{l}{g}}$

が成り立ちます。

この式をよく見ると、単振り子の周期 $T$ は、振れの角度 $\theta$ や物体の質量 $m$ に無関係であり、重力加速度 $g$ と、糸の長さだけで決まることがわかります。

これが、ガリレオの発見した

振り子の等時性ですね！

同じおもりをもちいて、重力加速度と糸の長さが変化しないのであれば、単振り子の周期 $T$ は、その振れ幅にかかわらず不変です。

ばね振り子

一方、ばね振り子と呼ばれるものがあります。(お詫び：式中の $m,k$ が逆でした。修正しました。) 

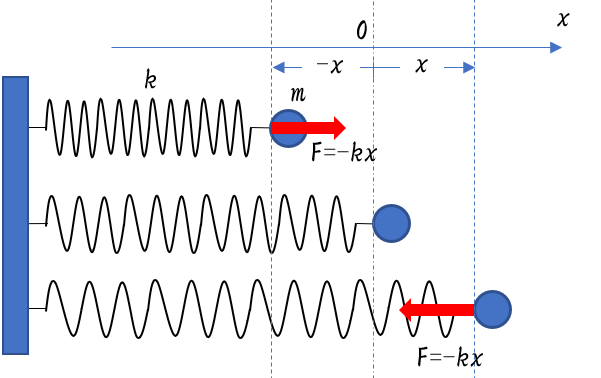
このばね振り子は、ばね定数 $k$ のばねに質量 $m$ の物体を付けたものです。

このとき、振動中心から $x$ だけ離れた位置で物体が受ける力は $F=-kx$　と示される単振動運動です。

したがって、

$F=-kx=-m\omega^2 x$

より、$\omega =\sqrt{\dfrac{k}{m}}$　です。

よって、その周期 $T$ は

$T=2\pi\sqrt{\dfrac{m}{k}}$ 

で示されるため、質量 $m$ とばねの固さを示すばね定数 $k$ に関係します。

しかし、振動周期 $T$ は、ばね振り子の振れ幅と重力加速 $g$ に無関係です。

つまり、

地上でばね振り子を振らせても、

月面で振らせても同じ周期になる！

ということですね。

まとめ

単振り子とばね振り子について簡単にまとめてみました。