アルベルト・アインシュタイン(1879 – 1955)は奇跡の年 1905年に「光量子仮説」「ブラウン運動の理論」「特殊相対性理論」に関連する五つの重要な論文を立て続けに発表しました。
一特許局の役人が世界を揺るがす理論を構築したのですね。
今回は彼の功績の中でものちのノーベル賞受賞につながった光電効果の理論について解説いたします。
光電効果
光電効果
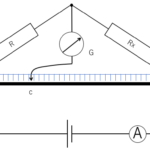
光電効果とは、よく磨いた金属の表面に光を当てると電子が飛び出してくる、という現象です。
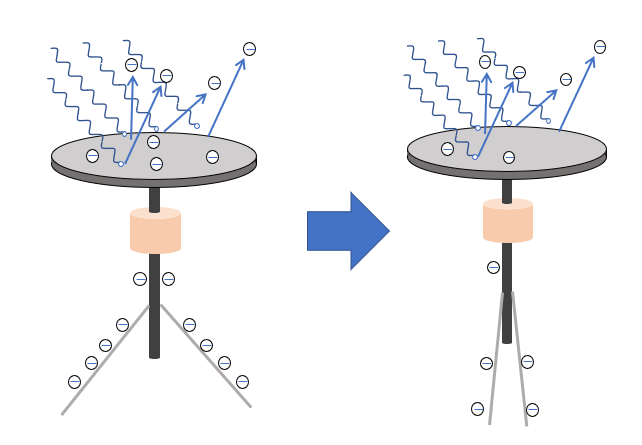
その飛び出してくる電子を光電子と呼びます。
このとき、
$h\nu=W+K_0$
が成り立つ。ただし、$K_0$:電子の運動エネルギーの最大値 $h$:プランク定数 $\nu$:光の振動数 $W$:仕事関数
限界振動数:$\nu_0=\dfrac{W}{h}$ 限界波長:$\lambda_0 = \dfrac{hc}{W}$
この実験事実自体は19世紀末に発見されていたのですが、古典物理学では説明がつかず放置されていたのです。
アインシュタインはこの論文を目にし、「ここには何かある」と直感的に思ったのかもしれません。
この研究に着手します。
光電効果のナゾ
光電効果の特徴的な性質について
- 金属板から光電子が出るかどうかは、あてる光の振動数による
ある振動数(限界振動数 $\nu_0$)以下ではどんなに強い光をあてても光電子は出ない - 限界振動数 $\nu_0$ を超えていれば、どんなに弱い光でも照射するとすぐに光電子が飛び出す
- 光電子の運動エネルギーの最大値 $K_0$ は、あてる光の振動数 $\nu$ による
- 限界振動数 $\nu_0$ 以上の光をあてるとき、どんなに光を強くしていっても $K_0$ は変化しない が、光電子の数は増加する
これらは古典的な波動論ではうまく説明ができなかったのです。
以下、なぜ古典論では説明できないかを示します。
- 金属板から光電子が出るかどうかは、あてる光の振動数による
ある振動数(限界振動数 $\nu_0$)以下ではどんなに強い光をあてても光電子は出ない古典的な波動論では、光のエネルギーは光の強度に比例するはずなので、限界振動数の説明ができない
- 限界振動数 $\nu_0$ を超えていれば、どんなに弱い光でも照射するとすぐに光電子が飛び出す
古典的な波動論では、弱い光のエネルギーは小さいのであててすぐに光電子が飛び出す説明ができない
- 光電子の運動エネルギーの最大値 $K_0$ は、あてる光の振動数 $\nu$ による
古典的には光電子の運動エネルギーはあてる光の強度に関係するはず
- 限界振動数 $\nu_0$ 以上の光をあてるとき、どんなに光を強くしていっても $K_0$ は変化しない が、光電子の数は増加する
古典的には、強い光をあてると光電子は大きなエネルギーを得るはずなので、最大エネルギー $K_0$ が変化しないことの説明ができない
これらの矛盾点を一気に解決するアイデアが次で解説する「光量子仮説」なのです。
光量子仮説
アインシュタインは光を、光子(光量子)と名づけた粒子であるとして、光電効果の理論的な説明に成功しました。
振動数 $\nu$ の光のエネルギー $E$ は、
$E=h\nu$
で示されます。$h$ はプランク定数とよばれる定数です。
いままで波であることが疑いがない、と思われていた光を粒子と考えたのです。
では、光が粒子であるとして、光電効果をどのように説明できるでしょうか。

逆に、粒子であることが間違いないと思われていた電子の波動性を考えたのが ド・ブロイ です。

アインシュタインの理論では、光子一つが $h\nu$ のエネルギーをもち、金属内にある電子にそのエネルギーをすべて与えて消滅します。
つまり、光子と電子が 1:1 で反応するとしたのです。
また、光電子が金属から飛び出すためには、金属原子からの束縛を断ち切るためのエネルギーが必要です。
これを仕事関数 $W$ といいます。$W$ の値は金属により異なります。
よってエネルギー保存則より、
$h\nu=W+K_0$
これが光電効果のアインシュタインの式です。
運動エネルギーの最大値 $K_0$ としているのは、実際には電子が原子などの束縛を断ち切るためのエネルギーは大きいものも小さいものあるため、飛び出してくる光電子の運動エネルギーに差が出るためです。
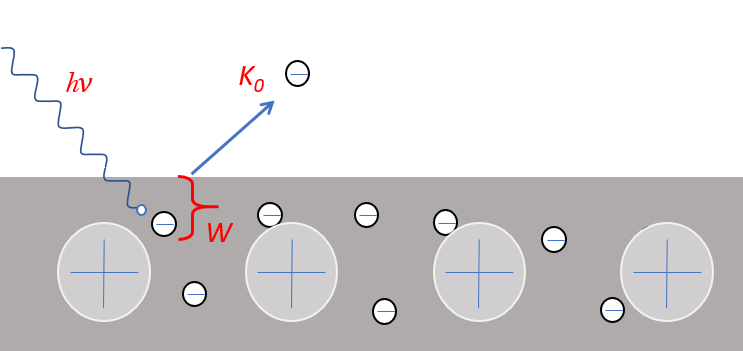
前にあげた光電効果の特徴を光子をつかって考えてみましょう。
- 金属板から光電子が出るかどうかは、あてる光の振動数による
ある振動数(限界振動数 $\nu_0$)以下ではどんなに強い光をあてても光電子は出ない光電子が飛び出すためには最低限、仕事関数に相当するエネルギーを電子に与える必要がある。
光子エネルギーは振動数 $\nu$ に比例するため、仕事関数 $W$ 以下のエネルギーしか持たない光子は光電効果を起こさない。 - 限界振動数 $\nu_0$ を超えていれば、どんなに弱い光でも照射するとすぐに光電子が飛び出す
光子と電子は 1:1 対応なので、限界振動数をこえて仕事関数 $W$ 以上のエネルギーを与えることができれば光電子はすぐに飛び出す。
- 光電子の運動エネルギーの最大値 $K_0$ は、あてる光の振動数 $\nu$ による
光子と電子は 1:1 対応であることから容易に説明できる。
つまり、振動数が大きくなると、電子1個に与えられるエネルギーが増大する。 - 限界振動数 $\nu_0$ 以上の光をあてるとき、どんなに光を強くしていっても $K_0$ は変化しない が、光電子の数は増加する
これも、光子と電子は 1:1 対応であることから容易に説明できる。
振動数を変えずに光を強くするとは、光子の数を増やすことになるため光電子の数は多くなる。しかし光子と電子は 1:1 対応であるため、振動数が同じであれば $K_0$ に変化はない。
もういちどアインシュタインの式から、
$h\nu=W+K_0$
より、光を金属板にあてたとき、かろうじて光電子が出る、つまり光電子の運動エネルギーが $0$ であるときが限界振動数となります。
したがって、限界振動数 $\nu_0$ は
$h\nu_0=0+K_0$
限界振動数:$\nu_0=\dfrac{W}{h}$
で示されます。これ以下の振動数では光電効果は起きません。
$c=\nu\lambda$ だから 限界波長:$\lambda_0 = \dfrac{hc}{W}$
光電効果のグラフ
ここで $h\nu=W+K_0$ を変形して
$K_0=h\nu-W$
として、縦軸を運動エネルギーの最大値 $K_0$ 、横軸を振動数 $\nu$ としてグラフを描いてみます。
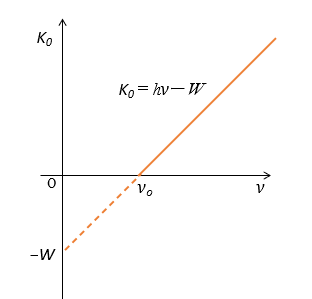
図のようなグラフが描けるはずです。
このグラフの傾きが、プランク定数 $h$ であることに注意してください。




































コメント