相対速度はわかってしまえばどうということはないのですが、ちょっと戸惑う概念です。
この記事で相対速度についてしっかり理解してくださいね。
もう間違えない!いい方法もお教えします。
相対速度でつまづいている人はいませんか?
一般に、ある物体から他の物体を見るときに相対速度を考えることができます。
まずは一直線上からいきましょう。
こちらもどうぞ!エッセンスの問題13番を題材に詳しく解説しています。
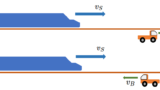
一直線上での相対速度例
例1
今、自転車AとトラックBが一直線上の道路で走っています。
自転車の速度を $20 \: \mathrm{km/h} $ 、トラックの速度を $40 \: \mathrm{km/h}$ 、ともに右向きとします。

このとき、自転車から見てトラックは、図の右向きに $20 \: \mathrm{km/h}$ で遠ざかるように見える!というのが相対速度の考え方です。
「いや~、そんなの言われてみればそうかもしれないけど、実際走っているときにそんな風には見えません」、といわれるかもしれませんが、それは、周りの景色や風などがあるからです。
もし、宇宙空間のように周りになにもなく真っ暗であったとすれば、自分が動いているかどうかなどは不確かなものになると思いませんか?
例2
ではこんどは、自転車の速度を $40 \: \mathrm{km/h} $ 、トラックの速度を $20 \: \mathrm{km/h}$ 、ともに右向きとします。

このとき、自転車から見てトラックは、図の左向きに $20 \: \mathrm{km/h}$ で近づくように見えます。
こういったときの計算方法は、
例1 右向き正として
自転車 A の速度 $V_A=+20 \: \mathrm{km/h} $ 、トラック B の速度 $V_B=+40 \: \mathrm{km/h}$
として、自転車 A から見たトラック B の速度 $V_{AB}$
$$V_{AB}= トラックの速度-自転車の速度= +40-(+20)=+20 $$
このときの $+$ は右向きを示します。したがって、自転車から見たトラックの速度は、図の右向きに $20\: \mathrm{km/h}$ となります。
このときトラックは $20 \: \mathrm{km/h}$ で遠ざかっていくように見えるのです。
例2 右向き正として
自転車 A の速度 $V_A=+40 \: \mathrm{km/h} $ 、トラック B の速度 $V_B=+20 \: \mathrm{km/h} $
として、自転車 A から見たトラック B の速度 $V_{AB}$
$$V_{AB}= トラックの速度-自転車の速度= +20-(+40)=-20 $$
このときの $-$ は左向きを示します。したがって、自転車から見たトラックの速度は、図の左向きに $20\: \mathrm{km/h} $ となります。
つまり自分が止まっていて、トラックが $20 \: \mathrm{km/h} $ でバックしてくるように見えるわけです。
これを一般式で表してみましょう。
一般に言えること

例1や例2で見たように、自転車 A から見たトラック B の速度 $V_{AB}$ について、
$$V_{AB}= V_B – V_A = トラックの速度-自転車の速度$$
と書くことができます。
ここでベクトルとして、図を書いてみましょう。
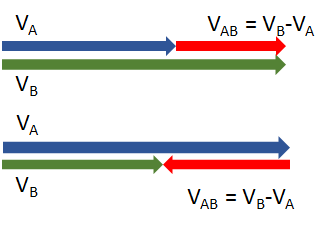
$V_A、V_B$ どちらのベクトルが大きくても $V_{AB}= V_B – V_A = トラックの速度-自転車の速度$ が成り立っています。
次のように考えると間違えません!
うまい方法!
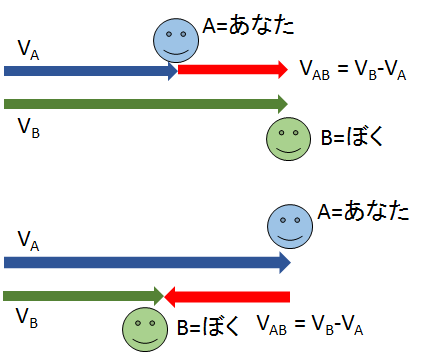
この考え方は、一直線上だけでなくあらゆる場合に使えます。
平面上の場合について相対速度を考えましょう。
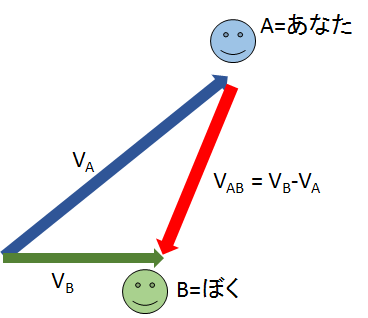
やはり
$A=あなた$ から $B=ぼく$ を見るように矢印を引けばそれが、$A=あなた$ から見た $B=ぼく$ の相対速度 $\overrightarrow{V_{AB}} $ となります。
平面上の場合の $\overrightarrow{V_{AB}}$ の大きさは、$V_B-V_A$ と単純に四則計算の引き算をしてはいけません。
ベクトル式で表すと、
$\overrightarrow{V_{AB}}=\overrightarrow{V_B} -\overrightarrow{V_A} $
この場合は、図形上の矢印の長さを計算する必要があります。
また、 $\overrightarrow{V_{AB}}$ の向きについても図形上で求めなければなりません。
相対的な関係は他に、相対加速度が考えられます。これについては別記事で。
また、物理のエッセンスの力学編 48 番の問題で動画解説しています。











































コメント