干渉条件などの公式?を丸暗記してはいけません。これは理解すべきもの。
そうでないと、応用がききません。
薄膜による光の干渉
子供の頃、濡れたアスファルトが油で虹色に光るのを見て、「油というのは薄くなるとこういう色をしているのか」‥‥と思っていました。
また、タマムシなど虹色に光る昆虫が、なぜそうやって光を放つのか不思議でたまりませんでした。

しかし後年、物理を学ぶとその原因は「薄膜」にある、ということがわかりました。
薄膜があるというだけで虹色に色付くのを非常に不思議に感じたのを覚えています。
これはシャボン玉の色づく現象も同じ理屈で、物理学では光の干渉という現象によって説明されます。

薄膜
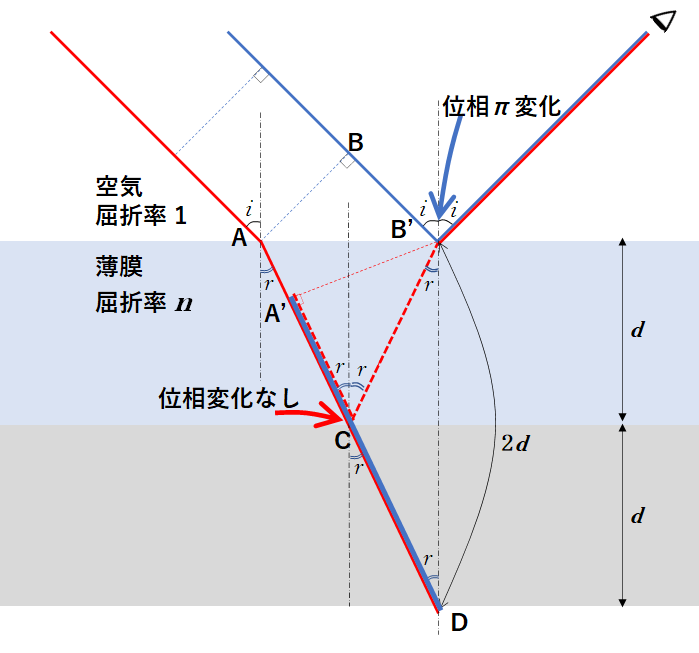
非常に薄い膜を考えます。(白色光の場合、膜が厚いと干渉条件に合致する光が多すぎて、干渉が観測できません)
そこに光が入射して薄膜内部で屈折反射した光と薄膜表面で反射した光が干渉します。
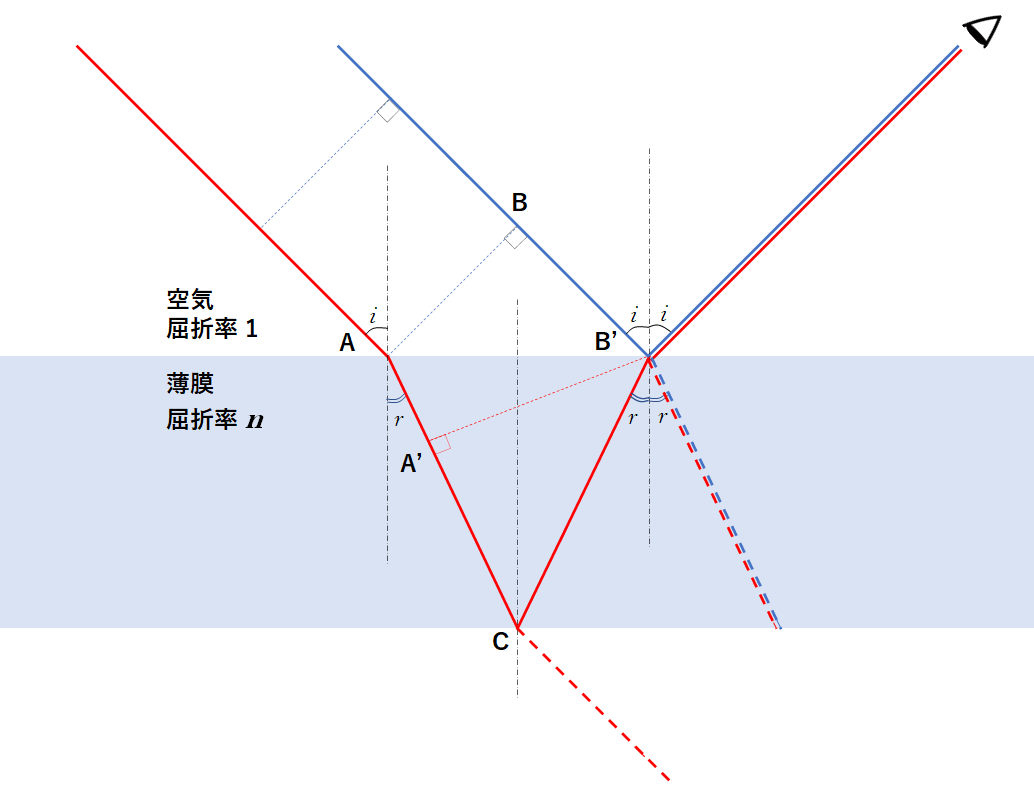
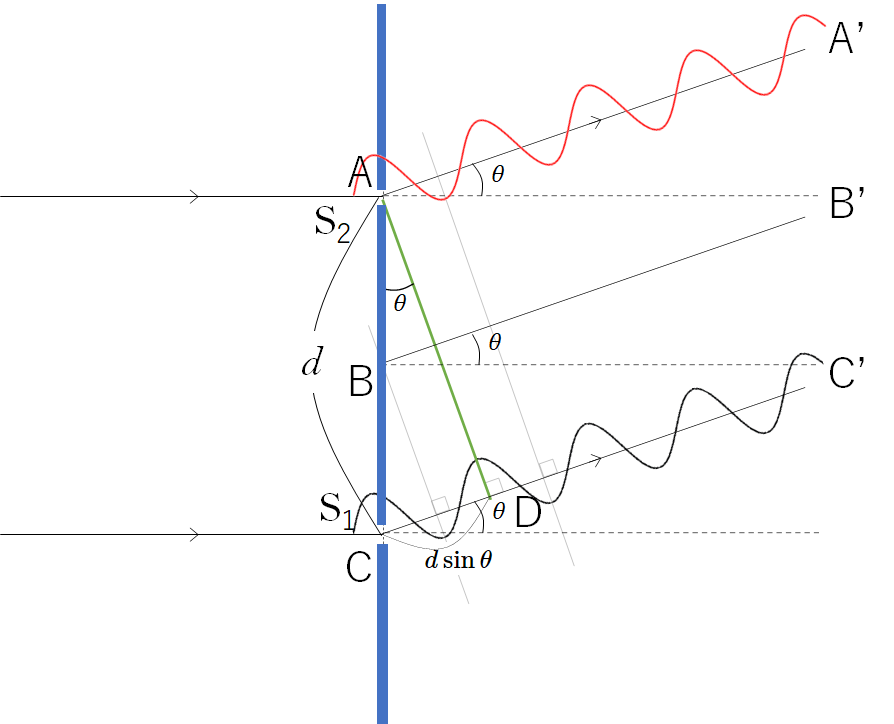
図は斜めから光が入射した場合を示しています。
波動の原理・理論はすべての波動で同じ(光も波動)ですから、現象の説明はすべて同じになるはずです。

物理というものは最小限の理論ですべてを説明することを試みるものです。
ここで、二重スリットの回折・干渉などで考えたことを思い出してください。

それによると、
二重スリットからの距離がそれぞれ $l_1$、$l_2$ にある点の干渉条件は次のようになります。波長: $\lambda$
明線 : $|l_1 – l_2| = m\lambda $
暗線 : $ |l_1 – l_2 |= m\lambda + \dfrac{1}{2}\lambda$
$m=0 , 1 , \:2 , \:3 \:\cdots\cdots$
ここでもう一度薄膜干渉の図を見ます。
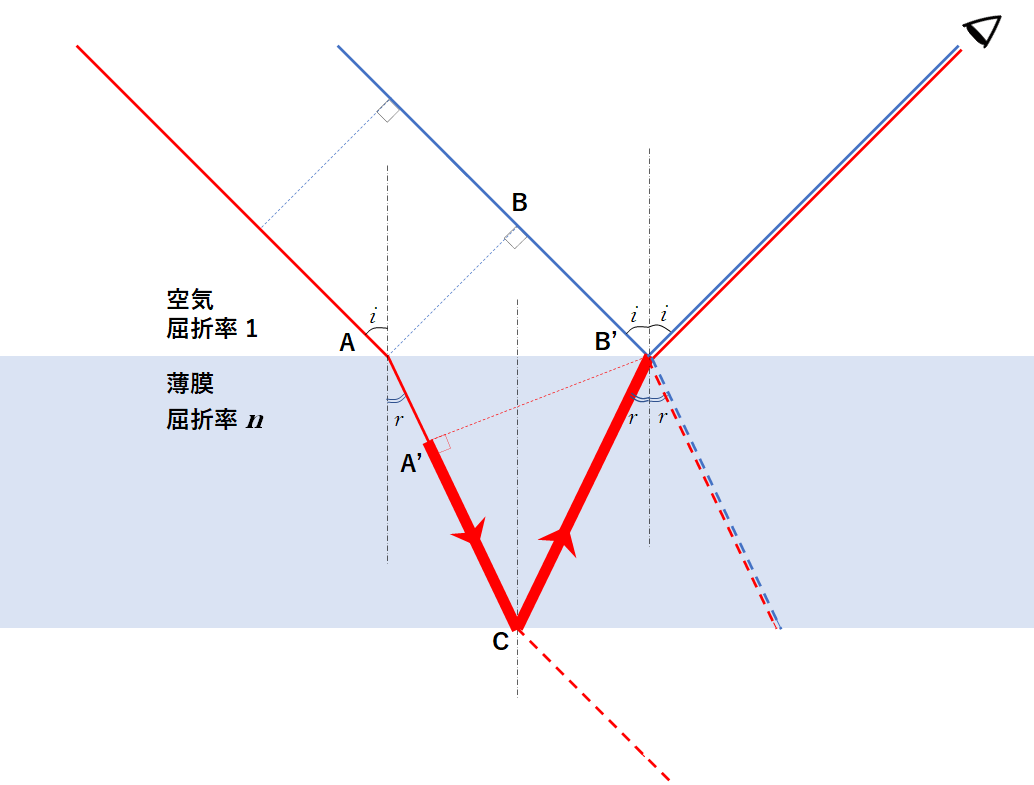
図の波面 AB および屈折後の波面 A’B’ は同位相です。
ともに平行・同位相で進んできた青と赤の光のうち、赤い光のほうが A’CB’ の長さの分だけ余分に進んで再び空気中に出、表面で反射した青の光と再び出会って干渉します。
赤の光は余分に進む距離、つまりこの A’CB’ の長さが、差 $ | l_1 – l_2 |$ に相当するというわけです。
したがって、先ほどの式で考えると、次のように考えられます。

物質中の波長を $\lambda^{\prime}$ としています。
これ、よく忘れるので気を付けてください。
あ、私だけかな?
注:反射に際して光の位相変化が考えられるため、ここでは暗線・明線の区別はしていません。
$ |l_1 – l_2 | =\mathrm{A’CB’} =m\lambda^{\prime} $
$ |l_1 – l_2 | =\mathrm{A’CB’}= m\lambda^{\prime} + \dfrac{1}{2}\lambda^{\prime}$
$m=0 , 1 , \:2 , \:3 \:\cdots\cdots$
位相変化
ここで大きな注意点があります。
それは反射に際して、光の位相に変化が起きるということです。
具体的には、
屈折率 小 ⇒ 屈折率 大 に行こうとして境界で反射する場合、反射光の位相は $\pi\:[\mathrm{rad}]$ だけずれる
ことがわかっています。
この位相が $\pi$ ずれる ‥‥ というのは何を意味しているのでしょうか。
位相とは、「波の状態を示すもの」・・・ という説明をよく見ますが、「なにそれ??」となる人も多いようです。
たしかにあいまいな表現だと思います。
詳しく言うと位相とは、波の媒質の各点が単振動している場合、「その単振動を示す参考円の回転角のこと」、です(次図)。
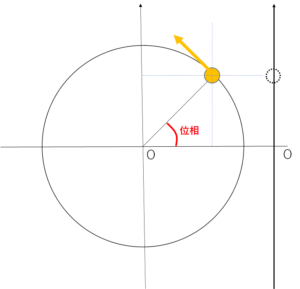
次に下の図をご覧ください。この回転角が $\pi$ ずれるということは、ずれたものは円のちょうど反対側であるということになります。
ちょうど反対側は 180° つまり $\pi$ ラジアンだけずれているということです。
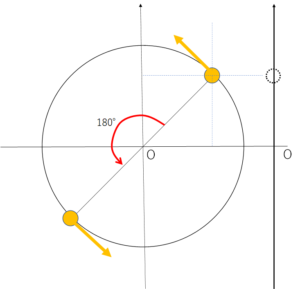
そうなると、今、単振動する点が最高点(波動の山)にきているとき、180° すなわち $\pi\:[\mathrm{rad}$ だけずれているところは参考円の下側、すなわち波動の谷にきていることになります。
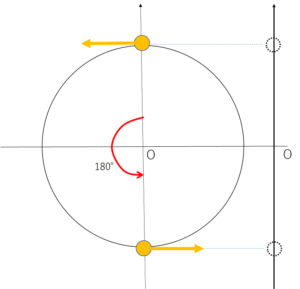
よって、光が 屈折率 小 ⇒ 屈折率 大 に行こうとして境界で反射する場合、反射光の位相は $\pi$ だけずれて、位相が反転する ような変化をしているというわけです。

注意
屈折率 大 ⇒ 屈折率 小 に行こうとして反射する波の位相はずれません。
これは
- 屈折率 大 ⇒ 光学的に密 ⇒ 振動しにくい ⇒ 固定端としてふるまう
- 屈折率 小 ⇒ 自由端としてふるまう
と考えてください。
薄膜の干渉条件
ではこの薄膜の干渉の場合、位相変化はどうなっているのでしょうか。
図の青の矢印のところで反射して位相反転していますが、赤の矢印のところでは位相はそのままです。

したがって、条件は逆転し、( $\lambda^{\prime} $ 物質中の波長)
暗線 : $ |l_1 – l_2 | =\mathrm{A’CB’} =m\lambda^{\prime} $
明線 : $ |l_1 – l_2 | =\mathrm{A’CB’}= m\lambda^{\prime} + \dfrac{1}{2}\lambda^{\prime}$
$m=0 , 1 , \:2 , \:3 \:\cdots\cdots$
となります。

注意ですが、薄膜の問題ではいつもこのようになる ・・・ としてこの式などを暗記してはいけません。
条件によっては、明線・暗線条件が逆転しない場合だってあり得ます。
そのつど、しっかり考えるようにしましょう。
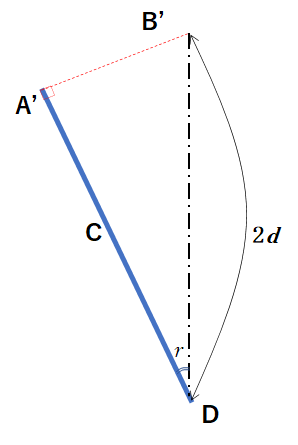
では、具体的に A’CB’ の長さを求めていきます。
次の図のように CB’ について薄膜の下の境界面で折り返してみます。
そうすると A’CB’ の長さ(図の赤の点線の部分)の長さは青色(A’CD)の長さに等しくなります。
そして A’CD は直線となります。
そうすると、直角三角形 A’DB’ において、
$\mathrm{A’CD} = 2d\cos r$
となります。次図
したがって、物質中の波長 $\lambda^{\prime}$ に注意して、
暗線 : $ \mathrm{A’CB’} =\mathrm{A’CD} = 2d\cos r= m\lambda^{\prime} $
明線 : $ \mathrm{A’CB’} = \mathrm{A’CD}= 2d\cos r= m\lambda^{\prime} + \dfrac{1}{2}\lambda^{\prime}$
$m=0 , 1 , \:2 , \:3 \:\cdots\cdots$
が成り立ちます。
これは屈折率 $n$ 中でのことなので、$\lambda^{\prime} = \dfrac{\lambda}{n}$
したがって、
暗線 : $ 2nd\cos r= m\lambda $
明線 : $2nd\cos r= m\lambda + \dfrac{1}{2}\lambda$
$m=0 , 1 , \:2 , \:3 \:\cdots\cdots$

屈折率 $n$ の物質中での長さ
・・・ 光路長 $2nd\cos r $ を考えても同じことですね。
位相が変化すると条件が入れ替わるのは
ところで、位相が $\pi$ 変化するとなぜ条件が入れ替わるのでしょうか?
ヤングの実験を思い出しましょう。
次の図で点 P で明線が観測されたとします。
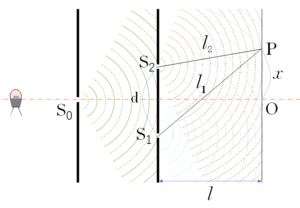
そうすると、スリットの部分を拡大してみた時、次の図のように行路差 CD に波が波長 $\lambda$ の整数倍( $m$ 倍)だけ入ればよい、ということはよろしいでしょうか。
もしも、下のスリットから出る光が何らかの理由で位相反転した場合、次の図のように行路差 CD に波が波長 $\lambda$ の整数倍( $m$ 倍)だけ入ると、今度は点 P では暗線になります。

なぜなら、AA’ と DC’ が等距離であり、A と D において位相が反転しているためです。





































コメント