交流電源を採用する理由の一つに、変圧の容易さが挙げられます。
今回解説する変圧器を使えば、交流の電圧を簡単に変えることができるのです。
このとき、一次コイルの巻き数を $N_1$ 、二次コイルの巻き数を $N_2$ とした場合、一次側の電圧実効値 $V_{1e}$ と2次側の電圧実効値 $V_{2e}$ は次の式に従います。
$V_{1e}:V_{2e}=N_1:N_2$
また、途中のエネルギー損失がないとすれば、一次コイル側と二次コイル側とで電力 $P_{1}$ と $P_{2}$が同じになります。よって、 $P_{1}=P_{2}$ より、次の式が成り立ちます。
$I_{1e}V_{1e}=I_{2e}V_{2e}$
これより、電流は巻数に反比例します。 $I_{1e}:I_{2e}=N_2:N_1$
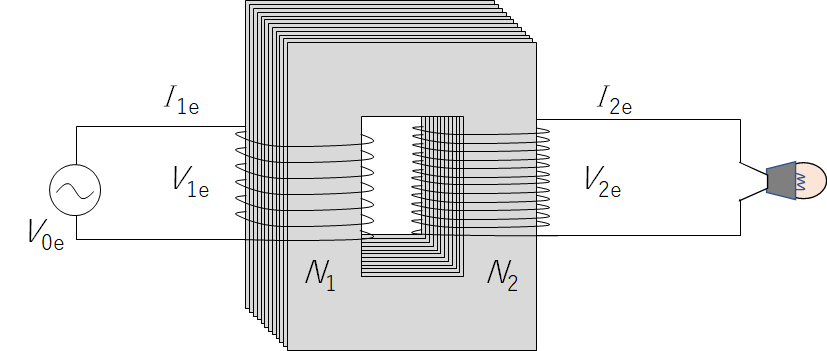
トランス 変圧器の原理
簡単に言えば、変圧器は鉄芯に導線を巻き付けてあるだけです。
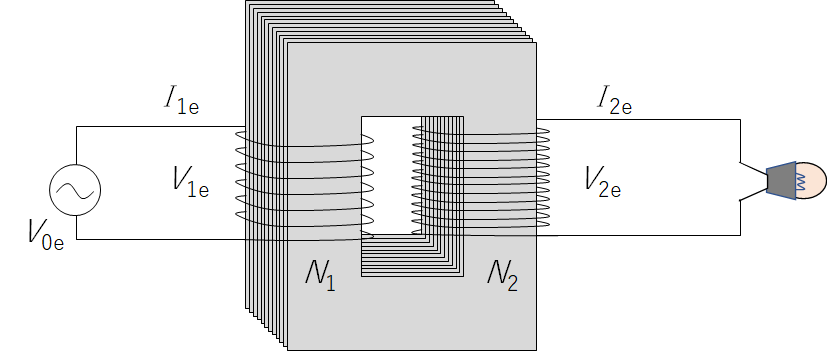
一次側に電源 $V_{0e}$ を接続してある場合を考えます。
一次側では自己誘導によりコイルに $V_{1e}$ の誘導起電力が生じます。

ファラデー電磁誘導の法則により、磁束が変化しなければ誘導起電力は生じません。
そのため、直流はこの変圧器では変換できません。
ここで、1次コイルの巻数 $N_1$ とします。
$\Delta t$ の間に磁束が $\Delta \Phi$ 変化したとすると、 ファラデー電磁誘導の法則から
$V_{1e}=-N_1\dfrac{\Delta \Phi}{\Delta t} \;\;\;\; \cdots \cdots \: (a)$
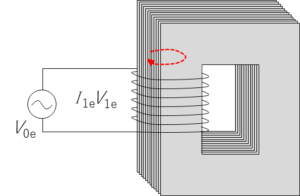
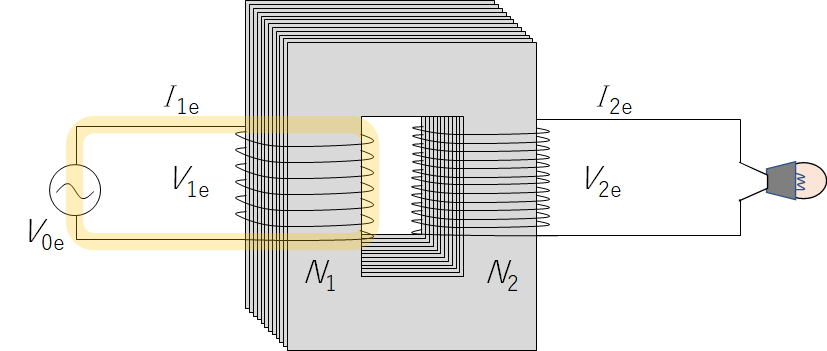
このとき、電源電圧との関係は、黄色で示した閉回路においてキルヒホッフの法則を適用すれば、
自己誘導による逆起電力が $-N_1\dfrac{\Delta \Phi}{\Delta t}$ であるから、 $\sum E=\sum {Ri}$ より
$V_{0e}-N_1\dfrac{\Delta \Phi}{\Delta t}=Ri$
このとき、 $R=0$ とすると、
$V_{0e}-N_1\dfrac{\Delta \Phi}{\Delta t}=0$
$V_{0e}=N_1\dfrac{\Delta \Phi}{\Delta t}$
となり、自己誘導起電力 $V_{1e}$ と電源電圧の大きさは等しい。
さらに、磁束線がコイル外に出ることがない理想的な変圧器では、コイル1の作り出す磁束のすべてが、コイル2をも貫くので磁束の変化 $\Delta \Phi$ はコイル1コイル2ともに共通となります。
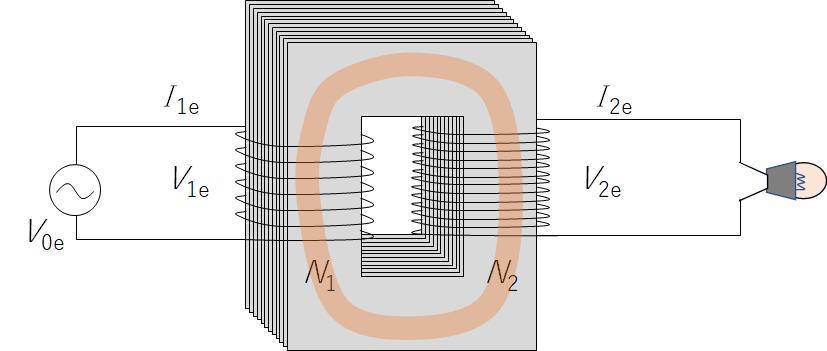
よって、ファラデー電磁誘導の法則から、( 2次コイルの巻数 $N_2$ )
$V_{2e}=-N_2\dfrac{\Delta \Phi}{\Delta t} \;\;\;\; \cdots \cdots \: (b)$
となります。
したがって、$(a)$ と $(b)$ より、
$V_{1e}:V_{2e}=\left| -N_1\dfrac{\Delta \Phi}{\Delta t} \right |: \left| -N_2\dfrac{\Delta \Phi}{\Delta t} \right |$
$V_{1e}:V_{2e}=N_1:N_2$
となり、電圧は巻数に比例します。

発電所から電気を送るには、いったん高電圧にして送り、さらに電圧を下げて家庭に入ります。
変圧器は複雑な装置を必要としません。
そのため、この変換の容易さが、交流を使う利点の一つです。
ではなぜ、わざわざ高圧にして送電するのでしょうか?
答えは記事の下部にあります。
変圧器のエネルギー
理想的な変圧器で、磁束が外部に漏れないとき、一次コイル側の電力 $P_{1} =I_{1e}V_{1e}$ と、二次側の電力 $P_{2 }=I_{2e}V_{2e}$ は保存されます。
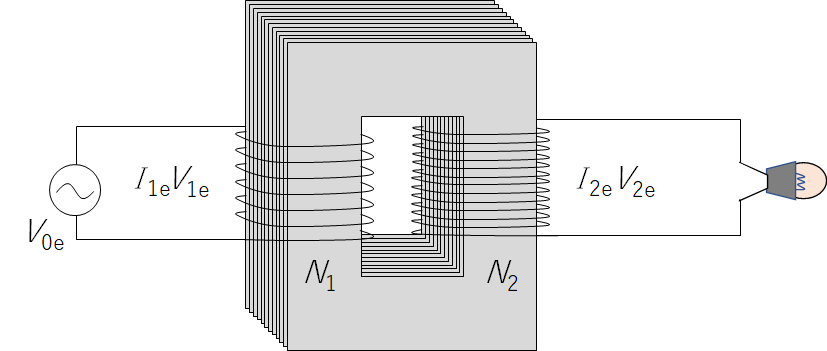
したがって、
$P_{1} =P_{2e}$
$I_{1}V_{1e}=I_{2e}V_{2e}$
となります。
また、 これらから
$I_{2e}:I_{1e}=V_{1e}:V_{2e}=N_1:N_2$
となります。
すなわち、電流は巻数に反比例します。

ちょっと疑問なんですが、
トランスは、鉄の塊ではなく、薄い鉄板を重ねて作るのはなぜでしょうか?

トランスは、渦電流によるエネルギーの損失を防ぐために、絶縁した鉄板を何層も重ねて鉄心を作っています。
高圧電線にする理由
電気を送るためには、いったん高電圧(数十万ボルト~)にしてから送り、再び 100 V や 200 V に戻しています。
なぜこのような面倒なことをする必要があるのでしょうか?
電圧を変換するのは、一つには送電線におけるエネルギーの損失を最小限に抑えるためです。
送電線での損失は $P=I^2R$ で示されるので、電圧を高くして電流 $I$ を小さくすることが有効です。
たとえば、電圧を100倍にすると電流は $\frac{1}{100}$ になり( 発電所の $P_0=I_eV_e=$ 一定 )、 送電線でのエネルギー損失は $P’=I_e^2R$ より、 $\frac{1}{10000}$ になります。
くわしくは、以下の記事を参考にしてください。





































コメント