2層の場合における、屈折による見かけの深さ
多層構造における見かけの深さの問題について考えてみましょう。
図にあるような2層からなる状態を考えます。
たとえば、水の上に油などが層をなして浮いているような状態です。
動画解説
考えてみよう
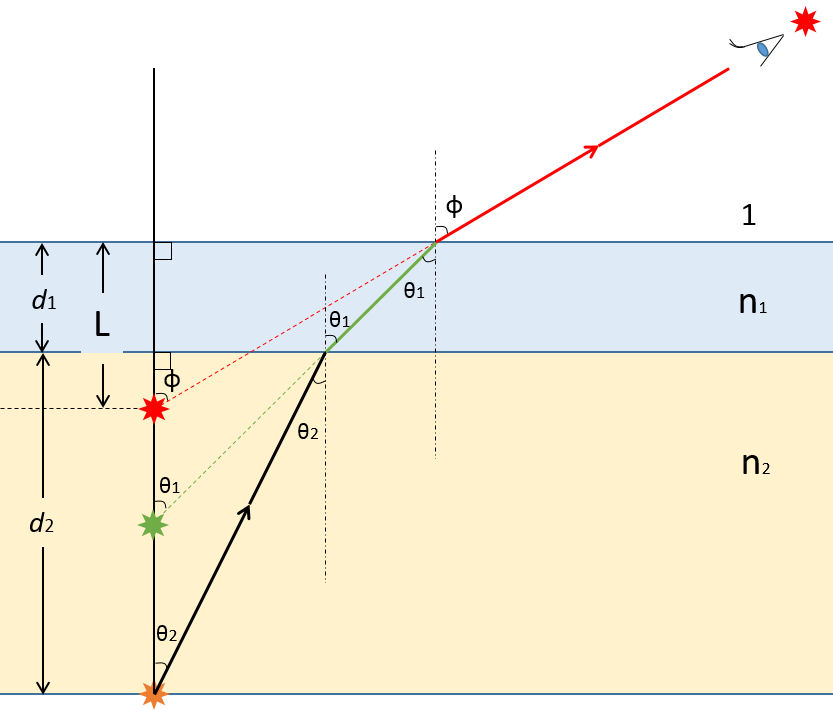
このとき、ほぼ真上から見た場合の、見かけの深さ $L$ について考えることにします。
このとき、実際は $d_1+d_2$ の深さに光源があるにも関わらず、$L$ の深さしかないように感じてしまいます。
屈折率は、$1<n_1<n_2$ とします。
では、まず下の $n_1$、$n_2$ の2層についての屈折の式をたてます。
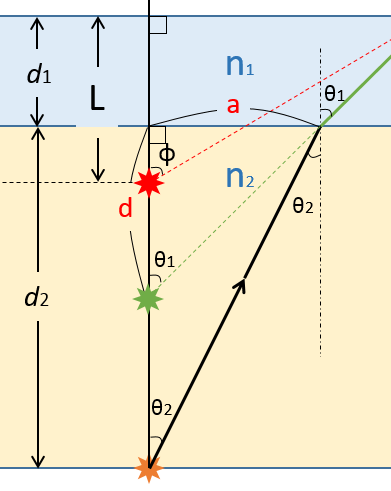
この場合、屈折の法則から、次の式が成り立ちます。
$$n_1\sin\theta_1=n_2\sin\theta_2$$

ここで、ほぼ真上から見ているという条件から、次の近似が成り立つとします。
$$\sin\theta \fallingdotseq \tan\theta$$
よって、
$$n_1\tan\theta_1 \fallingdotseq n_2\tan\theta_2$$
ここで、$\tan\theta_1=\dfrac{a}{d}$ 、$\tan\theta_2=\dfrac{a}{d_2}$ だから
$$n_1\dfrac{a}{d}=n_2\dfrac{a}{d_2}$$
より、
$$d=\dfrac{n_1}{n_2}d_2\:\:\cdots\cdots (1)$$
つづいて、空気と $n_1$ 層については、同様に次の図のように考えて
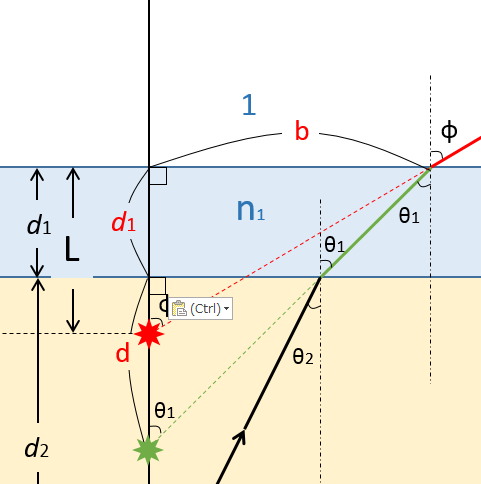
空気の屈折率が 1 なので、次の式が成り立ちます。
$$1\times\sin\phi=n_1\sin\theta_1$$
同じくほぼ真上から見ているため、$\sin\theta \fallingdotseq \tan\theta$ が成り立つとします。
ゆえに、
$$1\times\tan\phi \fallingdotseq n_1\tan\theta_1$$
ここで、$\tan\phi=\dfrac{b}{L}$ 、$\tan\theta_1=\dfrac{b}{d_1+d}$ だから
$$\dfrac{b}{L}=n_1\dfrac{b}{d_1+d}$$
$$L=\dfrac{1}{n_1}(d_1+d)$$
ここへ、(1) を代入して、
$$L=\dfrac{d_1}{n_1}+\dfrac{d_2}{n_2}$$
となり、見かけの深さが得られます。
私のオススメは、物理のエッセンス→良問の風→名問の森 です。






































コメント