メートルブリッジ
メートルブリッジは基本的にはホイートストンブリッジと同じです。
ホイートストンブリッジ
ホイートストンブリッジについてはこちらへ
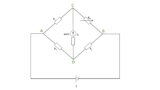
メートルブリッジ
メートルブリッジとは次のような図の装置です。
未知の抵抗 $R_x$ を測定するための器具です。抵抗 $R$ は既知とします。
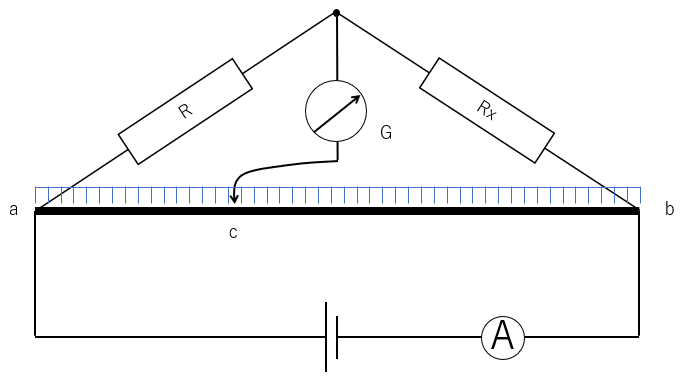
装置に電流を流しながら、探針を ab 上で動かして検流計Gに電流が流れない点 $c$ を探します。
そして、ac 、cb 間の長さを測定します。
ac 間の抵抗値 $R_{ac}$ と cb 間の抵抗値 $R_{cb}$ とすると。
ホイートストンブリッジの関係式を使って、
$R\times R_{cb}=R_x\times R_{ac}$
です。(割り算で示すなら、$\dfrac{R}{R_{ac}}=\dfrac{R_x}{R_{cb}}$)
ここで測定した、抵抗線 ac と抵抗線 cb の長さを、それぞれ $l_{ac}$ 、$l_{cb}$ とします。
抵抗値 $R$ は、導線の断面積 $S$ 、導線長さ $l$ 、比例係数 $\rho$ とした場合、
$R=\rho\dfrac{l}{S}$
で示されるので、導線が均一である場合は、
\begin{eqnarray}
R_{ac}:R_{cb}&=&\rho\dfrac{l_{ac}}{S}:\rho\dfrac{l_{cb}}{S}\\\\
&=&l_{ac}:l_{cb}
\end{eqnarray}
です。
したがって、
$R\times R_{cb}=R_x\times R_{ac}$
$R\times l_{cb}=R_x\times l_{ac}$
よって、
$R_x=\dfrac{l_{cb}}{l_{ac}}\times R$
より、未知の抵抗の抵抗値 $R_x$ を求めることができます。
応用例
この仕掛けはどこに使われていたのでしょうか?
意外なことに、昔の有線電話の故障診断に使われていたようです。
私も経験があるのですが、電話局に電話の故障連絡をすると、局で私の家の電話機の抵抗を測定して故障診断してくれました。
「抵抗測定してみますね。・・・・〇〇Ω出ていますので、正常です・・。」などと。
その仕掛けは、「たぶん、こうだったんじゃ?」と推測すると、次の図のようではないでしょうか。
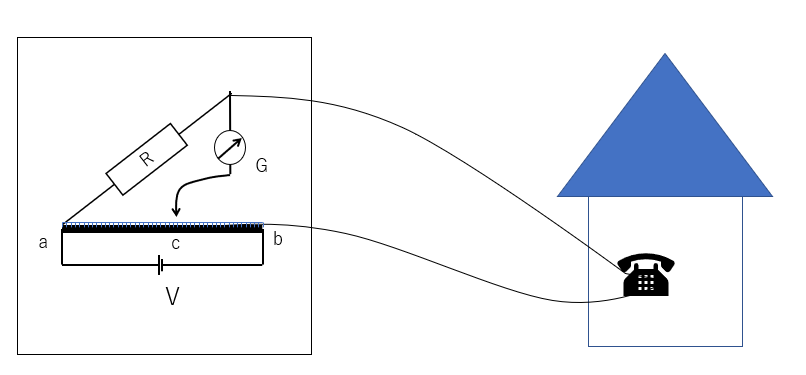
このようにすると、電話回線を使って、遠く離れた電話機器の抵抗値が、局にいながら測定できます。




































コメント