コイルに流れる電流が変化する場合、変化を打ち消す向きにコイルに誘導起電力が生じます。
これをコイルの自己誘導といいます。
自己誘導
コイルを含まない回路
次の図を見てみましょう。
図の黄色い回路に沿って電流が流れています。

この時の電流を $I_1$ とします。オームの法則から、
$I_1=\dfrac{V}{R_1+R_2}$
です。
次に、スイッチ S を閉じると、抵抗 $R_2$ はスキップされます。

回路を流れる電流はただちに変化して $I_2$ になります。
オームの法則から、
$I_2=\dfrac{V}{R_1}$
ですね。これらをグラフにしてみましょう。

スイッチ S を切り替えた瞬間、電流値が変化します。
コイルを含む回路
次に、図のようにコイルをつなげてみます。コイルの抵抗は無視できるものとします。
今、電池を接続してから十分な時間が経過した状態では、図の黄色い回路に沿って電流 $I_1$ が流れています。このとき、コイルは単なる導線とみなして構いません。

流れる電流は、 $I_1=\dfrac{V}{R_1+R_2}$ となるのは同じです。
次に、コイルを含んだ回路において、スイッチ S を閉じてみると、図の黄色の回路のようになるはずです。
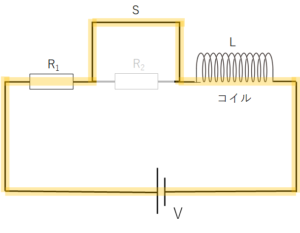
スイッチを閉じると抵抗 $R_2$ がスキップされるため回路の抵抗が減り、回路を流れる電流が増加します。
コイルがない場合は、この変化は瞬時に起こりました。
しかしコイルを含む場合には、次のグラフのように、電流はゆるやかに増加していきます。
これはコイルを貫く磁束が変化したため、コイルには逆起電力が誘導されるからです。

そこで、このときのコイルに生じる誘導起電力をグラフにしてみると次のようになります。
(ただし、電池の起電力の方向を正としている)
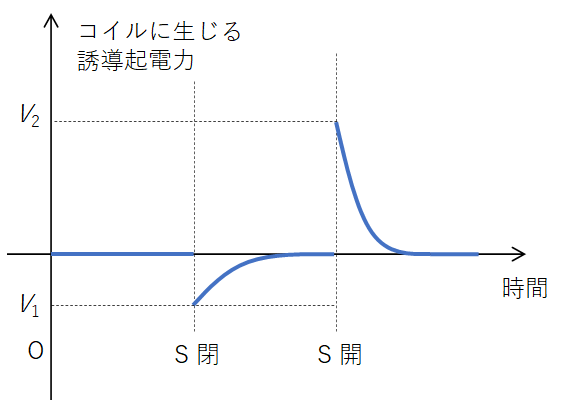
- スイッチ S を入れた瞬間
電池とは逆向きの起電力がコイルに誘導されます。
そのため、回路を流れる電流は定常状態の $I_2$ にまでゆっくりと変化します。 - スイッチ S を切った瞬間
電池と同じ向きの起電力がコイルに誘導されます。
そして、徐々に電流値が下がり $I_1$ まで変化します。
簡単に言えば、変化を緩和するような誘導起電力がコイルに生じるといえます。
このように、コイルに流れる電流が変化する場合、変化を打ち消す向きにコイルに誘導起電力が生じます。
このような現象を自己誘導と呼びます。

ひとこと
このようなコイルを含む回路で、
スイッチを切ったり入れたりした瞬間の、
コイルを流れる電流値は元の電流を維持しようとします。
自己インダクタンス
さて、コイルの自己誘導による誘導起電力 $V$ を求めてみましょう。
ソレノイドにおいて、

- ソレノイドの長さ $l$
- ソレノイドの単位長さ当たりの巻数 $n$
- 電流 $I$ が作る内部磁場の強さ $H=nI$
- 磁束密度 $B=\mu H= \mu nI$ ( 透磁率 $\mu$ )
- 磁束 $\Phi=BS=(\mu H)S=(\mu nI)S$
とした場合、微小変化 $\Delta$ を考えると、
$\Delta\Phi=\Delta(BS)$
$~~~~~~=\Delta(\mu nS I)\qquad \qquad\qquad \mu nS $ は一定のため、
$~~~~~~=\mu nS\Delta I$
となります。
このとき、ファラデー電磁誘導の法則からコイルに誘導される起電力 $V$ は次の式で示されます。
$V=-N\dfrac{\Delta \Phi}{\Delta t} \qquad \qquad\qquad \Delta \Phi=\mu nS\Delta I $ を代入
$~~~=-N\dfrac{\mu nS\Delta I}{\Delta t}$
ここで、 $L=N\mu nS=\mu n^2lS$ とおく( $N=nl$ $N$ はコイルの総巻数 )と、次の式が導出される。
$V=-L\dfrac{\Delta I}{\Delta t}$ この式は覚えておきましょう。
$V$:誘導起電力 $L$:自己インダクタンス $I$:電流 $t$:時間
つまり、誘導起電力 $V$ は、電流の変化の速さ $\dfrac{\Delta I}{\Delta t}$ に比例する。
ここで、負号 $-$ はレンツの法則を示している。
* 自己インダクタンス $L$ の単位には通常、 H(ヘンリー)を用いる。
コイルは、コイルに流れる電流が変化する場合、その変化を妨げる向きに誘導起電力 $V$ を生じ、その大きさは変化の速さが大きいほど大きくなる。






































コメント