- 交流と抵抗 交流の基礎 2 電磁気の記事は次を参照してください。 KoKo物理物理のエッセンス解説物理のクイズ物理の勉強方法物理実験過去問YouTubeチャンネルNEW 2025年共通テスト物理解説ワンポイント物理 このページ・力学 ・波動 ・熱力学 ・電磁気 ・原子物理 ・量子力学 ・物理数学力学 速度と...kokolainen.com ここでは交流と抵抗の関係について考えていきます。 交流電源と抵抗 $R$ をつないだだけの回路を考えましょう。 電源は $V=V_0\sin \omega t$ で変化するものとします。 キルヒホッフの法則より $V=RI$ よって、 $V=V_0\sin \omega t$ を代入して、 $I=\dfrac{V}{R}$ $~~~=\dfrac{(V_0 \sin \omega t)}{R}$ $~~~=\dfrac{V_0}{R}\sin \omega t$ ここで、 電流の最大値 $I_0=\dfrac{V_0}{R}\:\cdots\cdots\:(\ast)$ とすると、 $I=I_0 \sin \omega t$ この場合、抵抗を流れる電流と電圧の間には、コイルやコンデンサーで見られるような位相のずれはありません。 抵抗における消費電力 $P$ を考えます。 $P=IV$ であるから、 $I=I_0 \sin \omega t$ と $V=V_0\sin \omega t$ より、 $P=IV$ $~~~=(I_0 \sin \omega t)(V_0\sin \omega t)$ $~~~=I_0V_0 \sin ^2 \omega t$ $~~~=I_0V_0\dfrac{1-\cos 2\omega t}{2}$ $\cos (\alpha+\beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta $ $\beta=\alpha$ $\cos (2\alpha)=\cos ^2\alpha – \sin ^2\alpha $ $~~~~~~~~~=(1-\sin ^2\alpha )-\sin ^2\alpha $ $\sin ^2\alpha = \dfrac{1-\cos 2\alpha }{2}$ $\cos$ の値の時間平均は 0 であると考えられるため、 なぜって、これ足したら 0 ですよね。 平均の消費電力 $\overline{P}$ は、 $\overline{P}=I_0V_0\dfrac{1-\cos 2\omega t}{2} \: \cdots $ $\cos 2\omega t \: \rightarrow \: 0 $ として $~~~=\dfrac{1}{2}I_0V_0$ これを次のように変形します。 $\overline{P}=\dfrac{1}{\sqrt{2}}I_0 \times \dfrac{1}{\sqrt{2}}V_0$ ここで $I_e=\dfrac{1}{\sqrt{2}}I_0$ $V_e=\dfrac{1}{\sqrt{2}}V_0$ とし、これら $I_e$、$V_e$ を実効値と呼びます。 したがって、交流の消費電力は直流の場合と同様に、次のように表せます。 $\overline{P}=I_eV_e$ また、$(\ast)$ より、実効値、最大値ともに $V_0=RI_0$ $V_e=RI_e$ が成り立っています。 まとめ
- 次回
交流と抵抗 交流の基礎 2
電磁気の記事は次を参照してください。

ここでは交流と抵抗の関係について考えていきます。
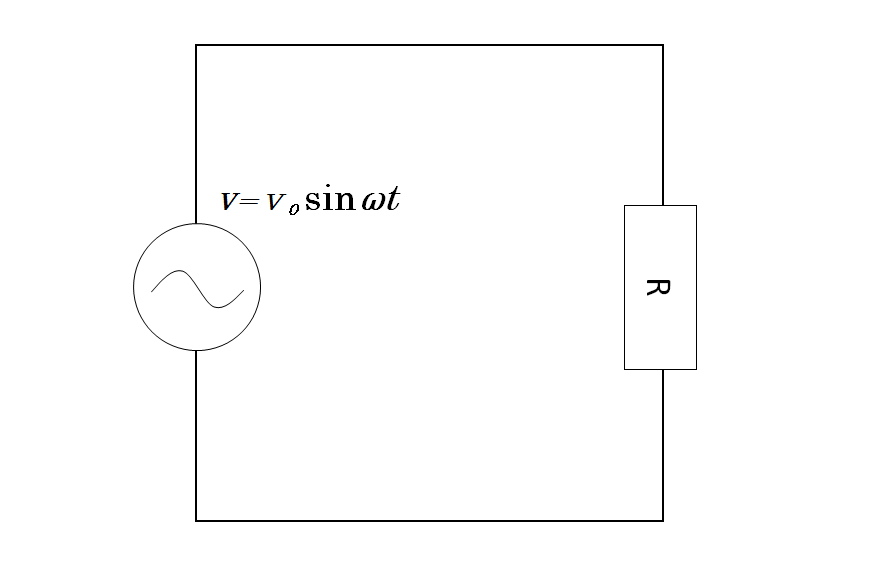
交流電源と抵抗 $R$ をつないだだけの回路を考えましょう。
電源は $V=V_0\sin \omega t$ で変化するものとします。
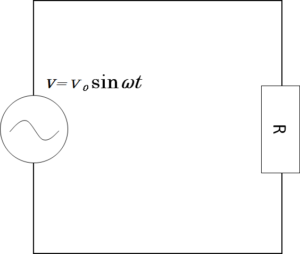
キルヒホッフの法則より $V=RI$
よって、 $V=V_0\sin \omega t$ を代入して、
$I=\dfrac{V}{R}$
$~~~=\dfrac{(V_0 \sin \omega t)}{R}$
$~~~=\dfrac{V_0}{R}\sin \omega t$
ここで、 電流の最大値 $I_0=\dfrac{V_0}{R}\:\cdots\cdots\:(\ast)$ とすると、
$I=I_0 \sin \omega t$
この場合、抵抗を流れる電流と電圧の間には、コイルやコンデンサーで見られるような位相のずれはありません。
抵抗における消費電力 $P$ を考えます。
$P=IV$ であるから、 $I=I_0 \sin \omega t$ と $V=V_0\sin \omega t$ より、
$P=IV$
$~~~=(I_0 \sin \omega t)(V_0\sin \omega t)$
$~~~=I_0V_0 \sin ^2 \omega t$
$~~~=I_0V_0\dfrac{1-\cos 2\omega t}{2}$

$\cos (\alpha+\beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta $
$\beta=\alpha$
$\cos (2\alpha)=\cos ^2\alpha – \sin ^2\alpha $
$~~~~~~~~~=(1-\sin ^2\alpha )-\sin ^2\alpha $
$\sin ^2\alpha = \dfrac{1-\cos 2\alpha }{2}$
$\cos$ の値の時間平均は 0 であると考えられるため、

なぜって、これ足したら 0 ですよね。

平均の消費電力 $\overline{P}$ は、
$\overline{P}=I_0V_0\dfrac{1-\cos 2\omega t}{2} \: \cdots $ $\cos 2\omega t \: \rightarrow \: 0 $ として
$~~~=\dfrac{1}{2}I_0V_0$
これを次のように変形します。
$\overline{P}=\dfrac{1}{\sqrt{2}}I_0 \times \dfrac{1}{\sqrt{2}}V_0$
ここで
$I_e=\dfrac{1}{\sqrt{2}}I_0$ $V_e=\dfrac{1}{\sqrt{2}}V_0$
とし、これら $I_e$、$V_e$ を実効値と呼びます。
したがって、交流の消費電力は直流の場合と同様に、次のように表せます。
$\overline{P}=I_eV_e$
また、$(\ast)$ より、実効値、最大値ともに
$V_0=RI_0$ $V_e=RI_e$ が成り立っています。
まとめ
- 電流と電圧の最大値 $I_0$ $V_0$



$\cos (\alpha+\beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta $
$\beta=\alpha$
$\cos (2\alpha)=\cos ^2\alpha – \sin ^2\alpha $
$~~~~~~~~~=(1-\sin ^2\alpha )-\sin ^2\alpha $
$\sin ^2\alpha = \dfrac{1-\cos 2\alpha }{2}$

なぜって、これ足したら 0 ですよね。

- 実効値 $I_e$ $V_e$
$I_e=\dfrac{1}{\sqrt{2}}I_0$
$V_e=\dfrac{1}{\sqrt{2}}V_0$
- 消費電力
実効値を使えば交流の消費電力 $\overline{P}$ は$\overline{P}=I_eV_e$
と示せます。
- オームの法則
$V_0=RI_0$ $V_e=RI_e$
次回
交流の基礎3 交流とコイル





































コメント