交流とコイル 交流の基礎 3
復習
電磁気の記事は次を参照してください。

今回は交流電源にコイルを接続した場合について考えていきます。
交流とコイル
ここでは交流とコイルの関係について考えていきます。
コイルは、自己誘導により逆起電力を発生します。
したがって、交流電流はコイルを通りにくくなります。
電源周波数が高いほど、磁束変化が激しくなるためコイルの抵抗成分は大きくなります。この点はコンデンサーとは反対です(こちらの記事参照)。
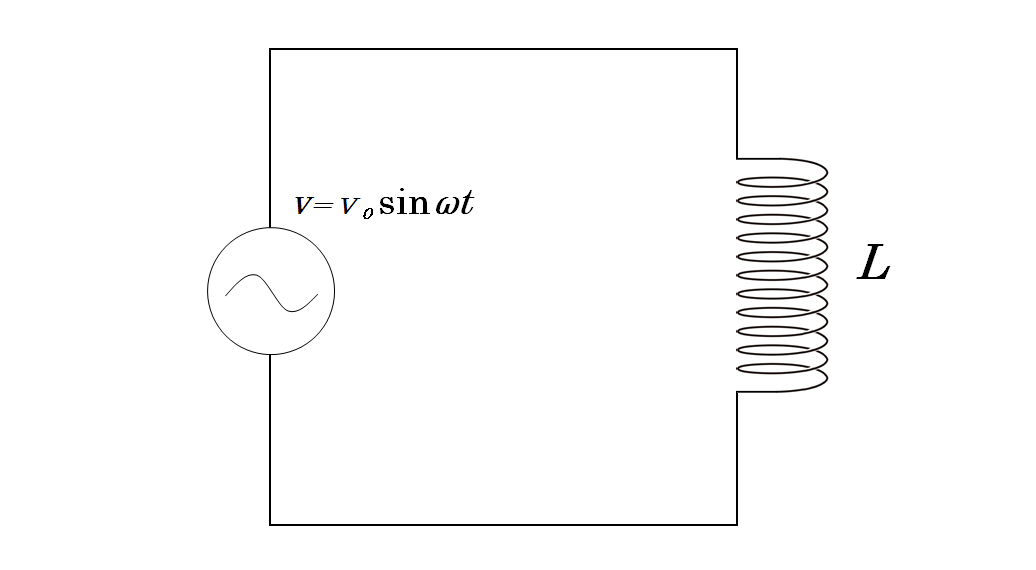
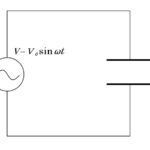
交流電源とコイル(自己インダクタンス $L$ ) をつないだだけの回路を考えましょう。
電源電圧は $V=V_0\sin \omega t$ で変化するものとします。

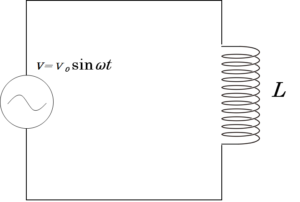
図の回路において、回路に流れる電流を $I_L$ とするとコイルでは逆起電力であることに注意して、キルヒホッフの法則を考えます。

すなわち、
$V_0\sin \omega t – L\dfrac{\Delta I_L}{\Delta t} = RI_L$
この場合、回路の抵抗 $R$ は 0 と考えられるので、
$V_0\sin \omega t – L\dfrac{\Delta I_L}{\Delta t} = 0 \times I_L $
よって、
$ V_0 \sin \omega t = L\dfrac{\Delta I_L}{\Delta t} $
この $\Delta$ を $\mathrm{d}$ と書き換えてみます。
$ V_0 \sin \omega t = L\dfrac{\mathrm{d} I_L}{\mathrm{d} t} $
これを $\int \mathrm{d}t$ すると、
$$\int V_0 \sin \omega t \:\mathrm{d}t=\int L\dfrac{\mathrm{d} I_L}{\mathrm{d} t} \mathrm{d}t $$
これより、
$-\dfrac{V_0}{ \omega} \cos \omega t = LI_L + C $
ゆえに、
$I_L=-\dfrac{V_0}{\omega L}\cos \omega t + C’ $
電源( $V=V_0 \sin \omega t$ )と比較するために $\cos$ を $\sin$ に書き直します。($C’$ は 0 として)

$-\cos \omega t = \sin(\omega t -\dfrac{\pi}{2})$
$I_L=\dfrac{1}{\omega L} V_0 \sin (\omega t -\dfrac{\pi}{2})=I_0 \sin (\omega t -\dfrac{\pi}{2})$
より、ここで電流の最大値 $I_0=\dfrac{1}{\omega L} V_0$ となります。
位相のずれ
これと、電源電圧の式 $V=V_0 \sin \omega t$ とを比較します。
とくに $\sin$ の中(位相)に注目します。
$V=V_0 \sin \omega t$
$I_L=\dfrac{1}{\omega L} V_0 \sin (\omega t -\dfrac{\pi}{2})=I_0 \sin (\omega t -\dfrac{\pi}{2})$
そうすると、 コイルを流れる電流 $I_L$ は電源に比べて、位相が $\dfrac{\pi}{2}$ だけ遅れていることに気がつきます。

覚え方
Coil の電流(i) は、遅れて(late)いる。
リアクタンス
ここでオームの法則( $V=RI$ )を思い出してみます。
$I=\dfrac{V}{R}$
$I_L=\dfrac{1}{\omega L} V_0 \sin (\omega t -\dfrac{\pi}{2})$
これらの式をじっくりと見ます・・・。
そうすると、オームの法則で示される抵抗 $R$ と同じ働きをするものがあることに気がつきます。
すなわち、
$ \dfrac{1}{\omega L} \: \Longrightarrow \:\dfrac{1}{R}$
よって、コイルをつないだ回路の抵抗成分 $X_L$ として
$X_L=\omega L$
とし、この抵抗成分 $X_L$ をリアクタンスと呼ぶことにします。
まとめ
位相
コイルを流れる電流の位相は、電圧の位相に対して $\dfrac{\pi}{2}$ 遅れている。
これを言い換えると、
コイルにかかる電圧の位相は、コイルを流れる電流の位相に対して $\dfrac{\pi}{2}$ 進んでいる。
とも書けます。
リアクタンス
交流回路におけるコイルの抵抗成分をリアクタンス $X_L$ とよび、
$X_L=\omega L$
で示される。
リアクタンス $X_L$ の値は $\omega$ や $L$ が大きいほど大きくなることがわかります。
$\omega = 2\pi f$ ですから、周波数の大きい電源ほどコイルの抵抗成分は大きくなります。
次回




































コメント